Variational Autoencoder(VAE)

约 1813 个字 4 张图片 预计阅读时间 6 分钟

Key

我在学习这部分时被大量的概率公式所困，以至于忘记了模型的初衷，所以在这里我直接放一下概念图以及核心思想

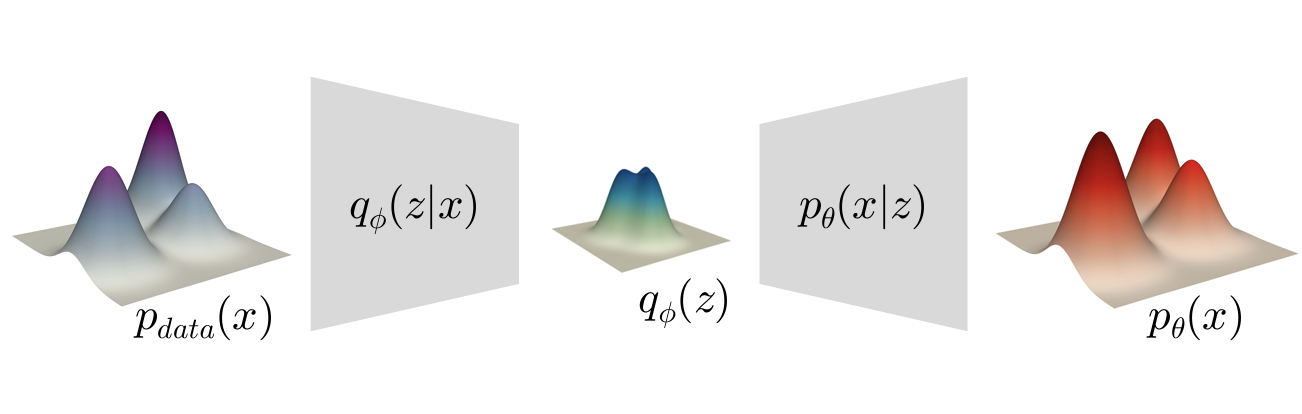
• 核心：

  通过编码器将输入数据映射到潜在空间，再通过解码器从潜在变量重构输入数据实现生成

Build

在概率模型中，我们希望计算数据的边际似然（marginal likelihood），即在给定观测数据\(x\)的情况下，计算其在潜在变量\(z\)上的边际分布。

\[ p_{\theta}(x) = \int p(x, z) dz = \int p_{\theta}(x|z) p(z) dz \]

但是：

• 这个积分往往是非常复杂甚至于不可解的
• \(p(z)\)是潜变量的分布，通常是不可观测（或者说很难得到正确的分布）

这时我们引入一个controllable的分布\(q(x)\)

变分分布

变分分布（variational distribution）是用于近似真实分布的一种分布。

在概率模型中，我们通常关心的一个问题是计算后验分布，即给定观测数据\(x\)后，潜在变量\(z\)的分布\(p(z|x)\)。根据贝叶斯定理：

\[ p(z|x) = \frac{p(x|z)p(z)}{p(x)} \]

这里对他计算十分不便，因为\(p(x)\)的积分非常复杂（尤其在\(p(x)\)是高维数据时）。

因此，我们引入一个变分分布\(q(z|x)\)，来近似\(p(z|x)\)，这个分布通常比较简单，且可以被控制。

变分推断

pick a variational parameter \(\phi\) so that \(q_{\phi}(z)\) is close to \(p_{\theta}(z|x)\)

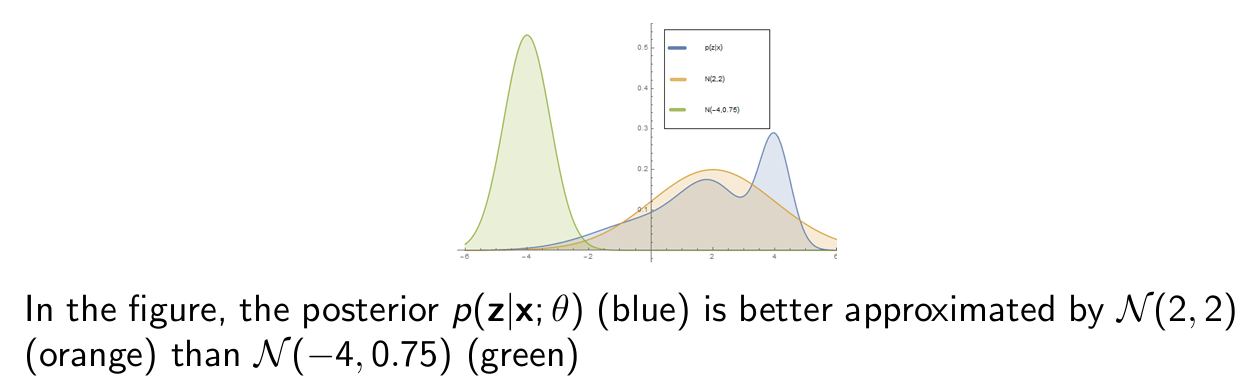
我个人的理解是，我们的优化对象是固定的，即\(p(x)\)，但在计算过程中，通常很难得到，所以这些工作都是在找一些近似方法来求解，至于我们能不能可视化的理解/从意义上理解这个分布我觉得可能不重要？

下面我推导完ELBO定义过程之后，可能会有更深的理解。

我们定义目标 最大化\(\mathcal{L}\) function:

\[ \mathcal{L}_{\theta,\phi(x)} = \mathbb{E}_{z \sim q_{\phi}(z|x)}[\log p_{\theta}(x|z)] - \mathcal{D}_{KL}(q_{\phi}(z|x) || p_(z)) \]

这个公式是在VAE中广泛采用的定义，同时也有一个形式更简单的（不打开\(p(x, z)\)）形式：

\[ \begin{aligned} \mathcal{L}_{\theta,\phi}(x) &= \sum_{z} q_{\phi}(z) \log p_{\theta}(z, x) + H(q_{\phi}(z)) \\ &= \mathbb{E}_{q_{\phi}(z)}[\log p_{\theta}(z, x) - \log q_{\phi}(z)] \end{aligned} \]

ELBO 的定义过程

首先对\(p(x)\)取对数，重写它在潜分布\(z\)上的对数似然

\[ \begin{aligned} \log p_{\theta}(x) &= \int_{z} q(z) \log p_{\theta}(x) dz \space \space \space \text{for any distribution q}\\ &= \int_{z} q(z) \log \frac{p_{\theta}(x|z)p_{\theta}(z)}{p_{\theta}(z|x)} dz \\ &= \int_{z} q(z) \log( \frac{p_{\theta}(x|z)p_{\theta}(z)}{p_{\theta}(z|x)} \frac{q(z)}{q(z)} ) dz \\ &= \int_{z} q(z)(\log p_{\theta}(x|z) + \log \frac{p_{\theta}(z)}{q(z)} + \log \frac{q(z)}{p_{\theta}(z|x)}) dz \\ &= \mathbb{E}_{z \sim q(z)}[\log p_{\theta}(x|z)] - \mathcal{D}_{KL}(q(z) || p_{\theta}(z)) + \mathcal{D}_{KL}(q(z)||p_{\theta}(z|x)) \end{aligned} \]

我们知道关于\(p(x)\)和基于x先验的z的项都是不易解决的（intractable）

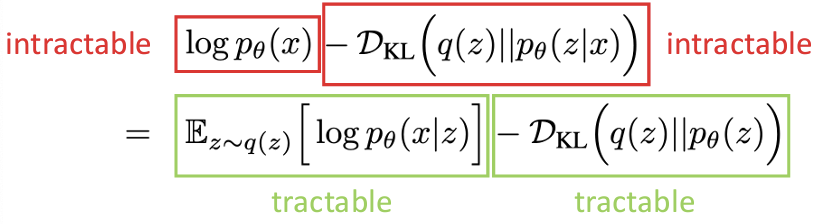
我们将这两块tractable的部分放在一起称为Evidence Lower Bound(ELBO)

最后我们在进行一步处理：

用参数化的\(q_{\theta}(z|x)\)代替\(q(z)\)，并将\(p_{\theta}(z)\)简单化处理为\(p(z)\)

其实好像还有一种非常简单的不等式处理方式，利用函数的convex性质和Jensen不等式，我们重写\(p_{\theta}(x)\)的log likelihood，然后再对得到的结果log展开即可

\[ \log p_{\theta}(x) = \log \sum_{z} p_{\theta}(x,z) = \log \sum_{z} q(z) \frac{p_{\theta}(x,z)}{q(z)} \geq \sum_{z} q(z) \log \frac{p_{\theta}(x,z)}{q(z)} = ELBO \]

这里的不等式当且仅当\(p_{\theta}(z|x) = q(z)\)时成立，这是因为选择不同的后验分布其逼近程度不同，从这里我们也可以看出，\(q(z)\)只要选择的好，那么\(ELBO\)的值就越逼近\(\log p_{\theta}(x)\)，也就是说 \(ELBO\)是对数似然\(\log p_{\theta}(x)\)的下界，哈哈！这不就是Evidence Lower Bound的含义吗！

取得等号即意味着KL散度为0

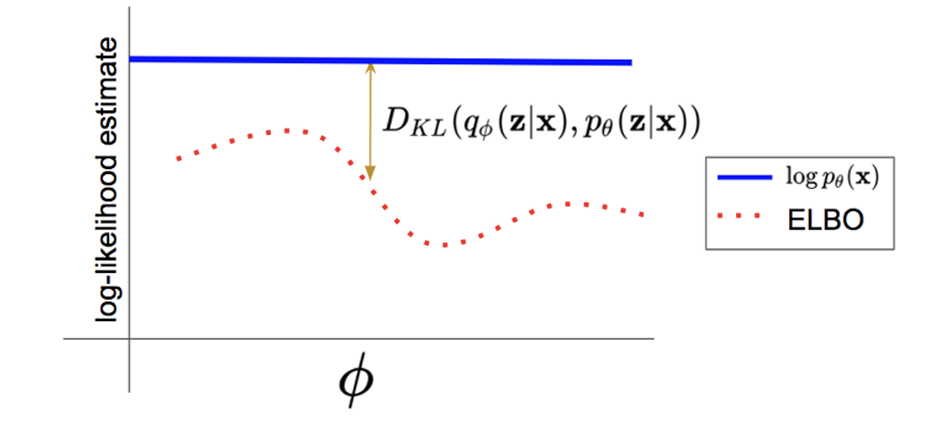
• Reconstruction Loss

  第一项\(\mathbb{E}_{z \sim q_{\phi}(z|x)}[\log p_{\theta}(x|z)]\)是重构对数似然项，用于衡量模型重构输入数据的能力，也就是模型能够生成与输入数据相似的数据的能力。

• Regularization Loss

  第二项\(\mathcal{D}_{KL}(q_{\phi}(z|x) || p_{\theta}(z))\)是正则化损失，用于约束潜在变量\(z\)的分布，表示变分分布\(q(z|x)\)与先验分布\(p(z)\)的差异，防止变分分布过度偏离先验分布。

Optimize

在前文中我们定义好了优化目标，现在我们看一些具体的优化问题：

• \(\phi,\theta\) 的优化

在Latent Variable Model中，我们提到了\(\theta\)是一个learnable的参数（在神经网络中学习），他被用作generator中，我的理解就是这里的\(\theta\)用作组合各个 潜变量然后输出一个预测分布\(p_{\theta}(x)\)

然后就是对变量\(\phi\)的理解：因为\(p_{\theta}(z|x)\)是intractable的，我们采用变分推断\(q_{\phi}(z)\)来逼近。而由于后验分布\(p_{\theta}(z|x^{i})\)对每个样本分布\(x^i\)是不一样的（例如飞机和大象的高阶特征不同），应该对每一个样本有一个variational parameter，得到优化目标就是：

\[ \max_{\theta, \phi^{1}, \phi^{2}, ...} \sum_{x^i \in D} \mathcal{L}(x^i, \theta, \phi^i) = \max_{\theta, \phi^{1}, \phi^{2}, ...} \mathbb{E}_{q_{\phi^i}(z)}[\log p_{\theta}(z, x) - \log q_{\phi^i}(z)] \]

现在我们用 Stochastic Variational Inference(SVI) 来进行优化：

就是使用随机梯度下降的变分推断

我们先前使用的\(\phi^i\)是单样本映射，但是由于参数过多很难训练，我们取一个amortized inference，也就是对全体样本都适用的一个\(\phi\)。

Amortization

通过学习一个单变量函数\(f_{\lambda}\)，将输入的每个样本\(x^i\)映射到一组好的变分参数

区别就是单样本映射需要对每个样本单独计算参数，而amortized inference通过训练神经网络将输入直接映射到共享参数

总的算法流程如下：

Algo

• Initialize \(\theta\) and \(\phi\)
• Randomly sample a data \(x^i\) from dataset \(\mathcal{D}\)
• Compute gradient \(\nabla_{\theta} \mathcal{L}\) and \(\nabla_{\phi} \mathcal{L}\)
• Update \(\theta\) and \(\phi\) in the direction of the gradient
• Repeat until convergence

现在来看具体的梯度计算：我们使用Monte Carlo来近似

可以看到\(\theta\)的梯度计算是直接的：

\[ \nabla_{\theta} \mathbb{E}_{q_{\phi}(z)}[\log p_{\theta}(z, x) - \log q_{\phi}(z)] \approx \frac{1}{K} \sum_{k=1}^{K} \nabla_{\theta} \log p_{\theta}(z_k, x) \]

但是\(\phi\)的梯度计算需要使用reparameterization trick：

Reason

我们知道所求期望是依赖于\(\phi\)的，对\(z\)的采样操作是不连续的，无法使用backpropagation，如果把采样操作转移到不需要backpro的部分，我们就可以只需要对参数求导

具体的方法如下：

假设\(z\)属于正态分布，将其改写：

\[ z = \mu + \delta \epsilon = g(\epsilon, \phi) \text{ g is determinstic} \]

其中\(\epsilon \sim \mathcal{N}(0, I)\)是一个标准正态分布的噪声项，\(\mu\)和\(\delta\)是学习的参数

Expectation Maximization

这部分是关于VAE模型与EM之间的关系

Vector Quantized(VQ-VAE)

留言

欢迎在下方交流~