跳转至

Score-based Models

约 3899 个字 25 张图片 预计阅读时间 13 分钟

Intro

在上一个模型Energy-based Models中，我们通过构建score matching来训练EBMs，好处就是我们不再需要关心pdf是否是标准化的（因为不需要计算partition function），只需要考虑梯度：

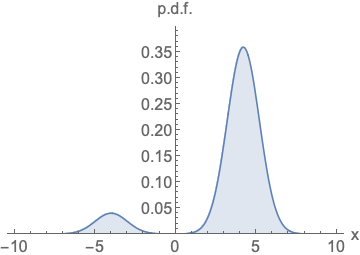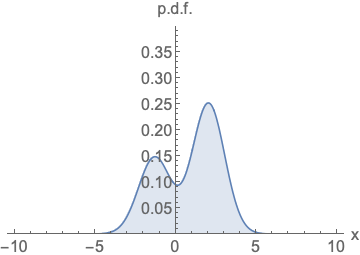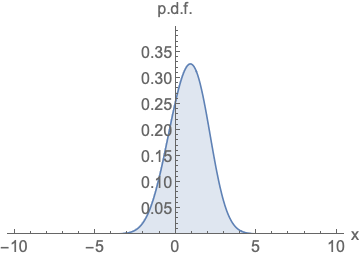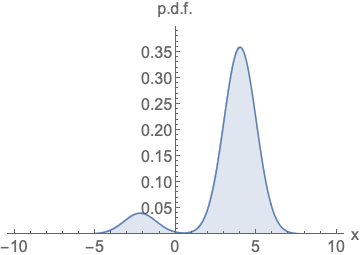
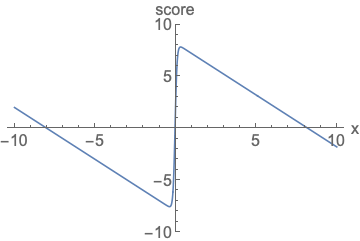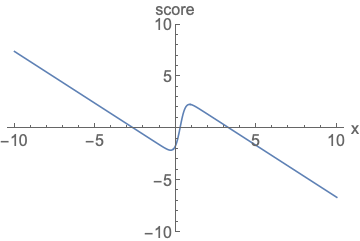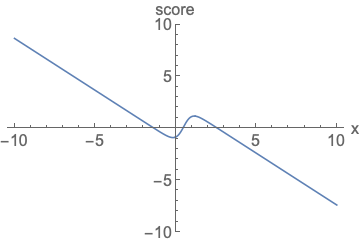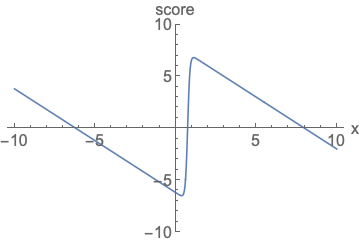
可以看到右边的梯度曲线，无需考虑面积问题，我们不再使用density来衡量模型，而是使用score

但是可以看到Fisher divergence是一个定义好的函数，不局限在EBM的训练中，所以我们可以将EBM的训练推广到score-based models中

在score-based models中，我们不再考虑一个能量（或者说在EBM的训练目标中\(f_\theta\)是一个标量函数，类似于势能），而是直接构建一个vector field of gradient，这时我们的对象就不仅是标量函数了，而是arbitrary vector fields

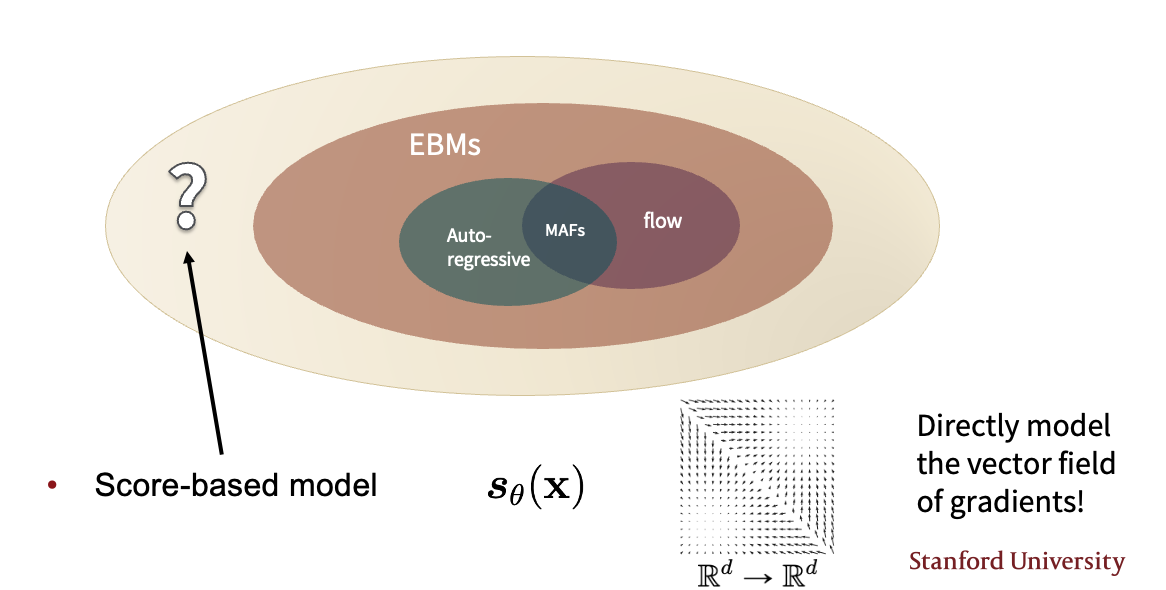
现在我们来重申一下score-based models的任务：

  • Given: i.i.d. samples\({x_1, x_2, \cdots, x_n} \sim p_{data}(x)\)
  • Task: Estimating the score \(\nabla \log p_{data}(x)\)
  • Score Model: A learnable vector-valued function \(s_\theta(x)\)
  • Goal: \(s_\theta(x) \approx \nabla \log p_{data}(x)\)

也就是

\[ \begin{aligned} &\min_\theta \frac{1}{2} \mathbb{E}_{x \sim p_{data}} \| \nabla_{x} \log p_{data}(x) - s_\theta(x) \|_{2}^2 \\ &=\min_{\theta} E_{\mathbf{x} \sim p_{\mathrm{data}}}[\frac{1}{2}\left\|\mathbf{s}_\theta (\mathbf{x})\right\|_2^2+\operatorname{tr}(\underbrace{\nabla_{\mathbf{x}}^2 \mathbf{s}_\theta(\mathbf{x})}_{\text {Jacobian of } \mathbf{s}_\theta(\mathbf{x})})] \end{aligned} \]

但是这个式子中的雅各比矩阵的trace很难计算

Not Scalable!

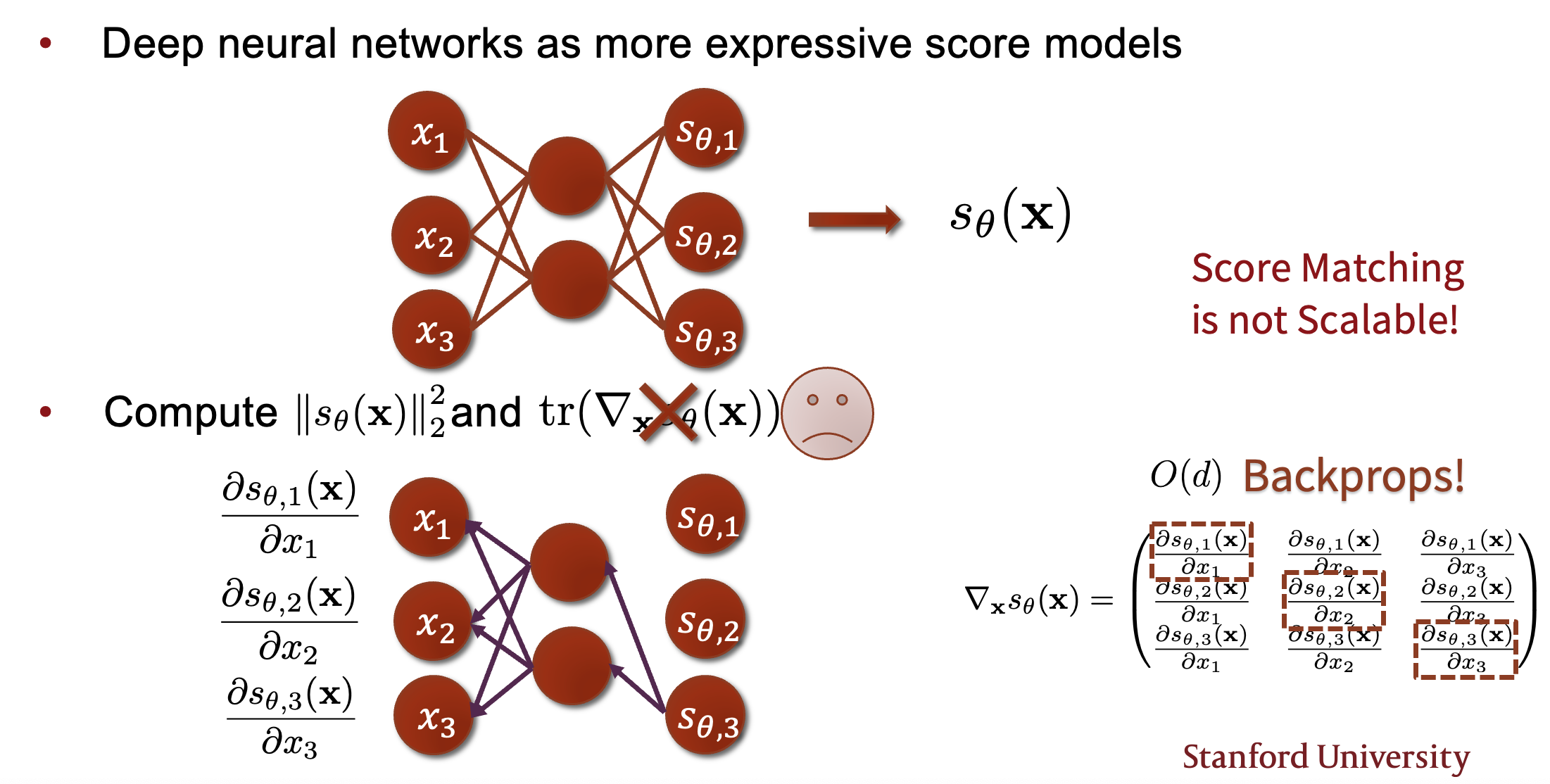
所以我们需要接下来的方法进行优化

Denoising Score Mathching

总体的思想是：我们不再对原先的\(p_{data}\)进行估计，而是对原始数据加入噪声后，对加入噪声后的数据\(\tilde{x}\)进行估计

设置噪声：

给定原始数据分布 \(p_{data}(x)\)，加噪后的数据\(\tilde{x}\)通过以下条件分布生成：

\[ q_{\sigma}(\tilde{x} | x) = \mathcal{N}(x; \tilde{x}, \sigma^2 I) \]

即\(\tilde{x} = x + \delta z, z \sim \mathcal{N}(0, I)\)

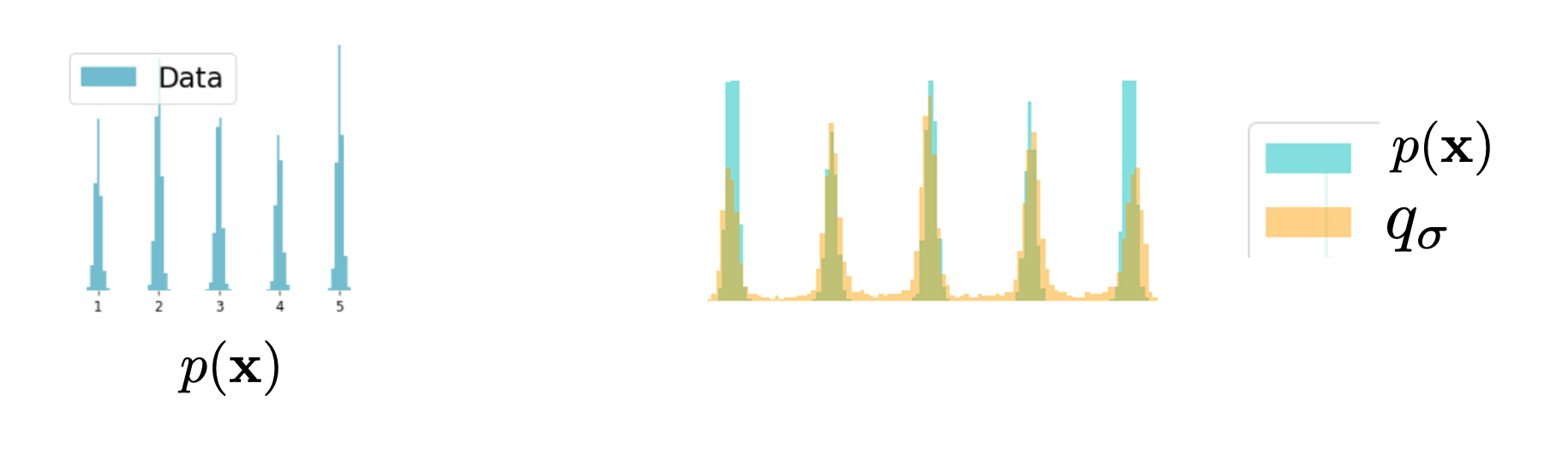
扰动后的边际分布是原始分布与噪声的卷积：

\[ p_{\sigma}(\tilde{x}) = \int q_{\sigma}(\tilde{x} | x) p_{data}(x) d\tilde{x} \]

现在我们来看score matching的优化目标，进行化简得到：

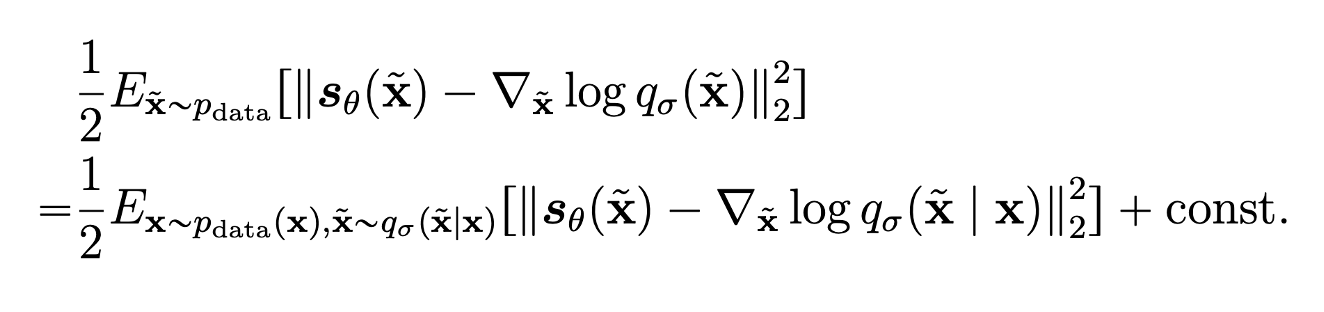
Prove

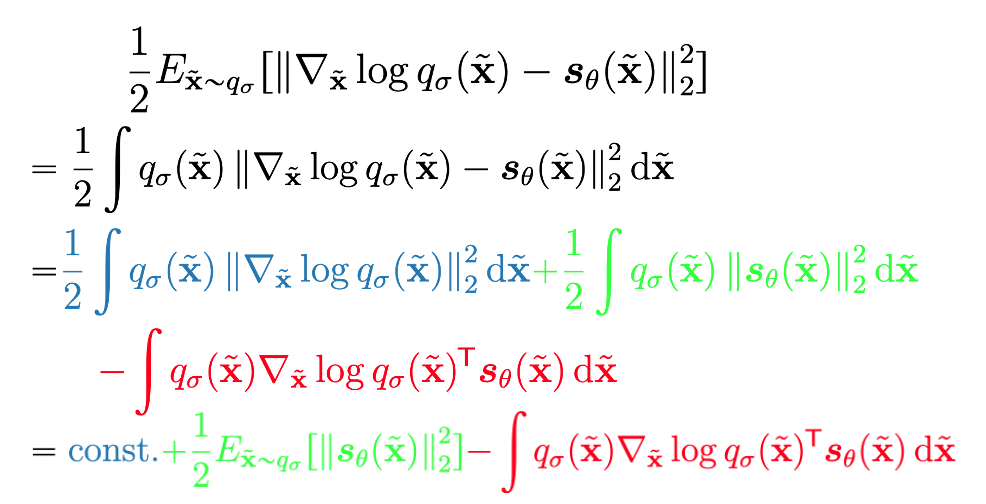
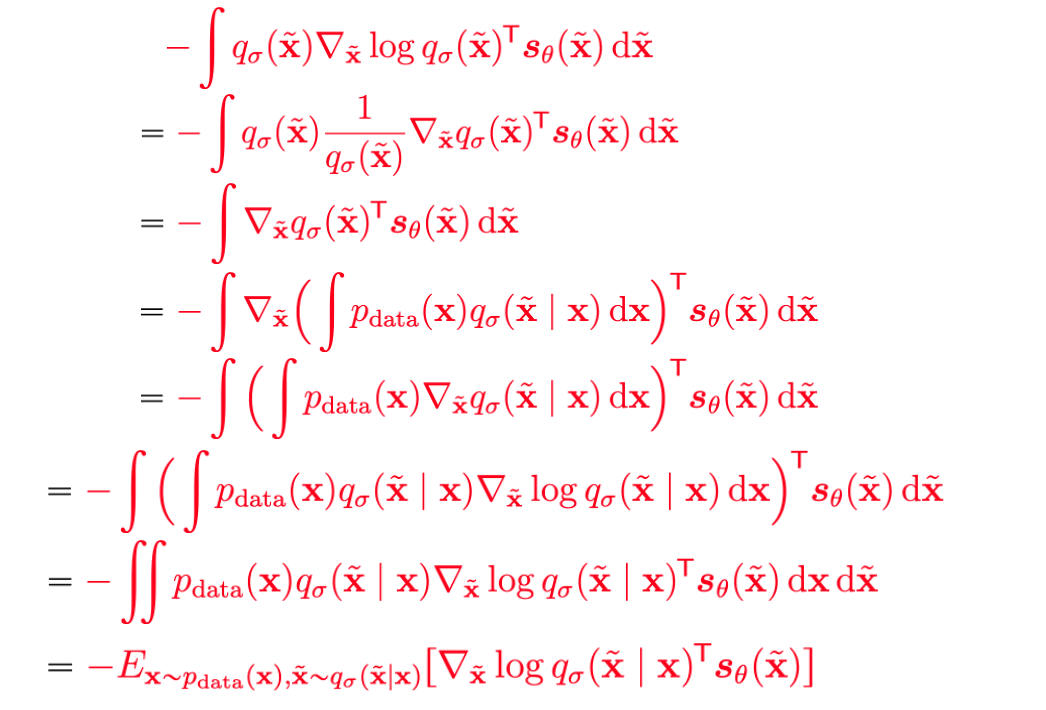
这里的化简就是将\(q_{\sigma}(\tilde{x})\)展开，然后利用他的线性性将gradient移到里面，随后重写这一项（加个log），方便将积分变为关于两个变量的期望

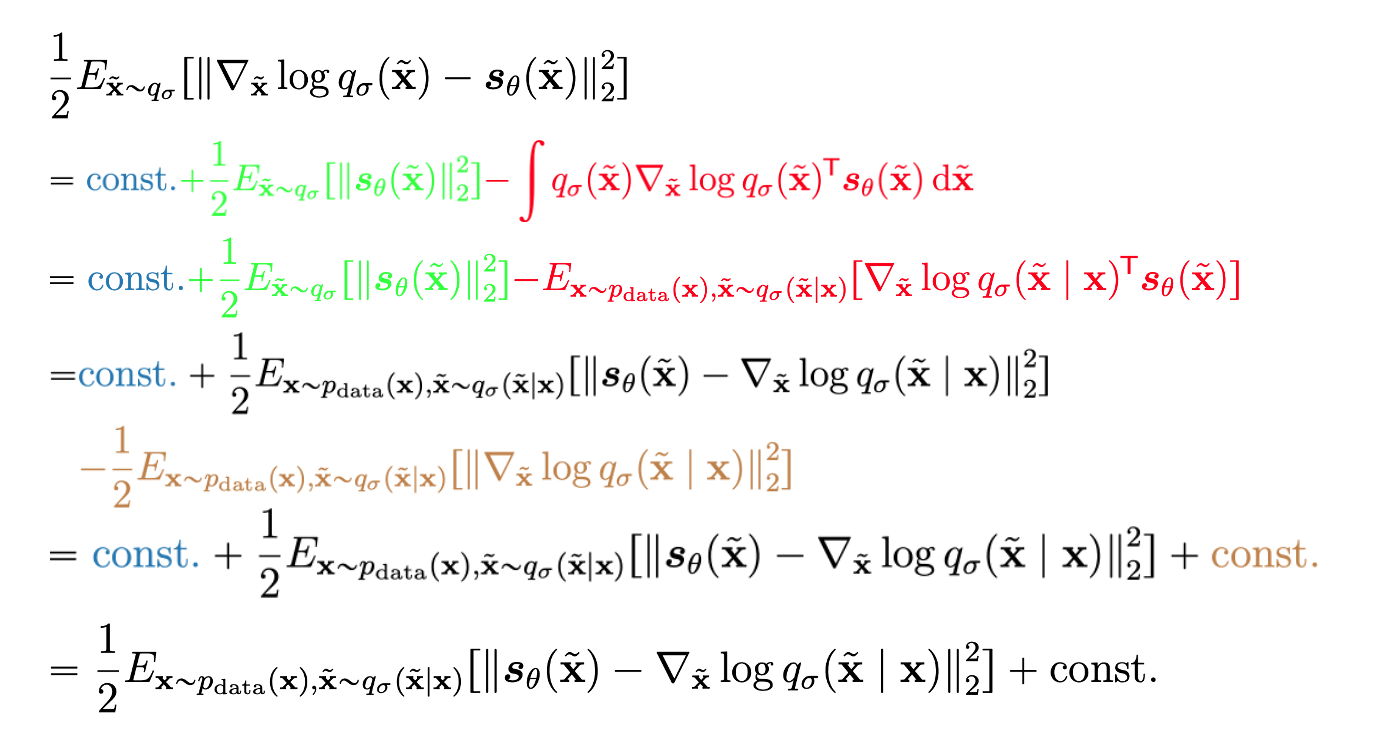
因为我们取q是Gaussian的，所以现在就有\(\nabla_{\tilde{x}} \log q_{\sigma}(\tilde{x} | x) = \frac{\tilde{x} - x}{\sigma^2}\)

  • Pros: efficient for high-dimensional data
  • Cons: cannot estimate the score of clean(original) data

回顾一下整个流程，我们将score matching的优化目标进行化简，得到（高斯噪声下的）denoising 形式

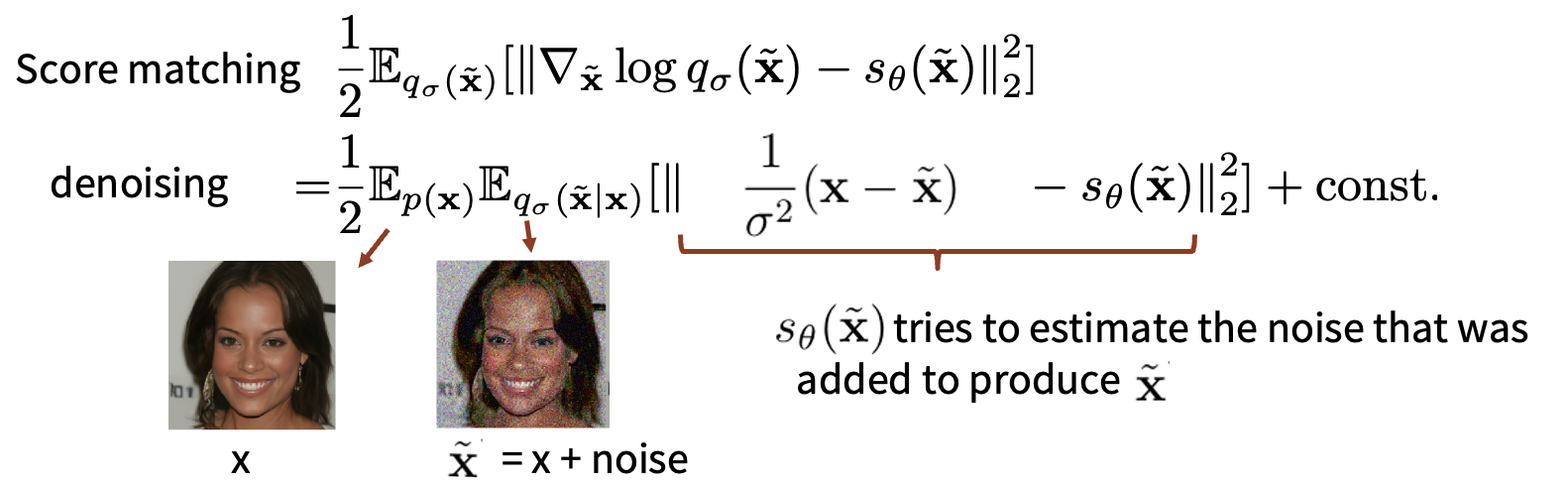
如何理解这个denoising呢？

我的理解就是在不知道\(p_{data}\)的情况下，尽量让分数间接匹配原始数据分数，可以看到公式中的\(s_\theta\)就是要在\(\delta \to 0\)时逼近\(\nabla \log q_{\sigma}(\tilde{x} | x)\)

草 我无法说服自己了

换个角度考虑，我们在思考optimal training object的时候，会发现上面我说的是成立的（也就是“尽量”）的意思，就是指怎么让未化简的公式和化简后的公式从逻辑上等价（因为化简前score是需要逼近扰动后的数据梯度，但化简后score看起来逼近的是噪声的梯度）

这里引入一个定理

Tweedie's formula

Optimal denoising strategy is to follow the gradient:

\[ \begin{aligned} E_{\mathbf{x} \sim p(\mathbf{x} \mid \tilde{\mathbf{x}})}[\mathbf{x}] & =\tilde{\mathbf{x}}+\sigma^2 \nabla_{\mathbf{x}} \log q_\sigma(\tilde{\mathbf{x}}) \\ & \approx \tilde{\mathbf{x}}+\sigma^2 \mathbf{s}_\theta(\tilde{\mathbf{x}}) \end{aligned} \]

就是说，给出加噪后的图像，清晰图像的预期值符合上面的公式

Sliced Score Matching

对于高维数据进行score matching时，计算雅各比矩阵的trace非常困难，所以需要进行近似，在这里我们想到一种方式将高维数据降维，通过随机投影（projection）

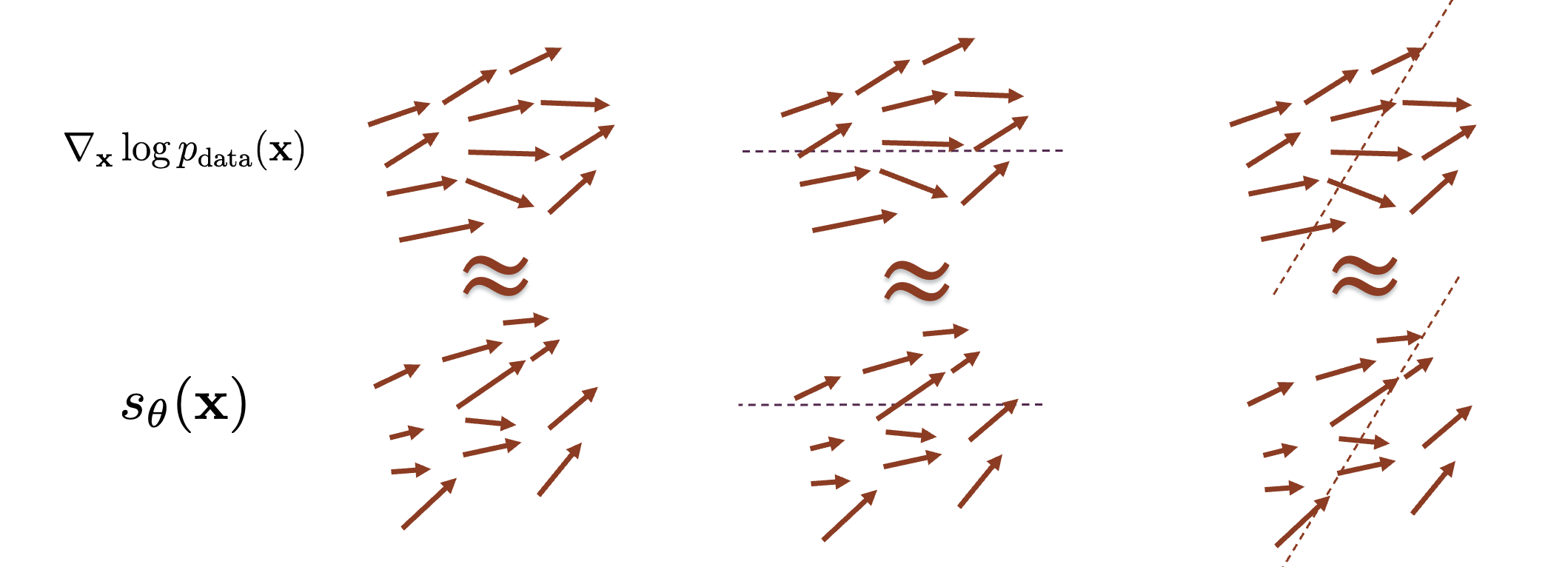
我们假设将两个分数（真实和预测）投影到随机向量\(v\)上后如果他们相等，那么就认为两个分数相等

\[ \begin{aligned} &\frac{1}{2} E_{\mathbf{v} \sim p_{\mathbf{v}}} E_{\mathbf{x} \sim p_{\text {data }}}\left[\left(\mathbf{v}^{\top} \nabla_{\mathbf{x}} \log p_{\text {data }}(\mathbf{x})-\mathbf{v}^{\top} \mathbf{s}_\theta(\mathbf{x})\right)^2\right]\\ &\text { Integration by parts :}\\ &E_{\mathbf{v} \sim p_{\mathbf{v}}} E_{\mathbf{x} \sim p_{\text {data }}}\left[\mathbf{v}^{\top} \nabla_{\mathbf{x}} \mathbf{s}_\theta(\mathbf{x}) \mathbf{v}+\frac{1}{2}\left(\mathbf{v}^{\top} \mathbf{s}_\theta(\mathbf{x})\right)^2\right] \end{aligned} \]

这里的\(\mathbf{v^T}\)与\(\mathbf{s_\theta}\)的乘积（点乘）是一个标量，所以最终我们得到的结果是一维的，通常我们随机选取\(v\)，可以从\(p_v\)（Gaussian、Rademacher中采样）中采样

现在来解释一下为什么计算这里的\(\mathbf{v^T \nabla_{x} s_\theta \mathbf{v}}\)是scalable的

Tip

  • 第一步前向传播计算\(\mathbf{s_\theta}\)
  • 第二步通过投影将\(\mathbf{s_\theta}\)降维到一维
  • 通过一次反向传播来计算这个标量对于所有输入的梯度
  • 再取一个点积将这个梯度降到一维
  • Pros:
    • 同样是more scalable
    • 是对clean data的score估计
  • Cons:
    • slower than denoising sm

Inference

我们知道可以按照分数的梯度方向进行采样，但是那样数据分布会完全收敛到一个单点，所以需要引入噪声

采用Langevin dynamics MCMC进行推理：

\[ \tilde{\mathbf{x}}_{t+1} \leftarrow \tilde{\mathbf{x}}_t+\frac{\epsilon}{2} \mathrm{~S}_\theta\left(\tilde{\mathbf{x}}_t\right)+\sqrt{\epsilon} \mathbf{z}_t \]

但是这种naive的方式效果非常差，原因有以下几点：

  • Manifold hypothesis: 数据分布在低维流形上，当数据逐渐收敛时，我们的分数会失去定义

    可以看到即使PCA降维后，样本仍没有太多变化

  • 数据密度在不同区域不同，会在低数据密度区域迷失方向

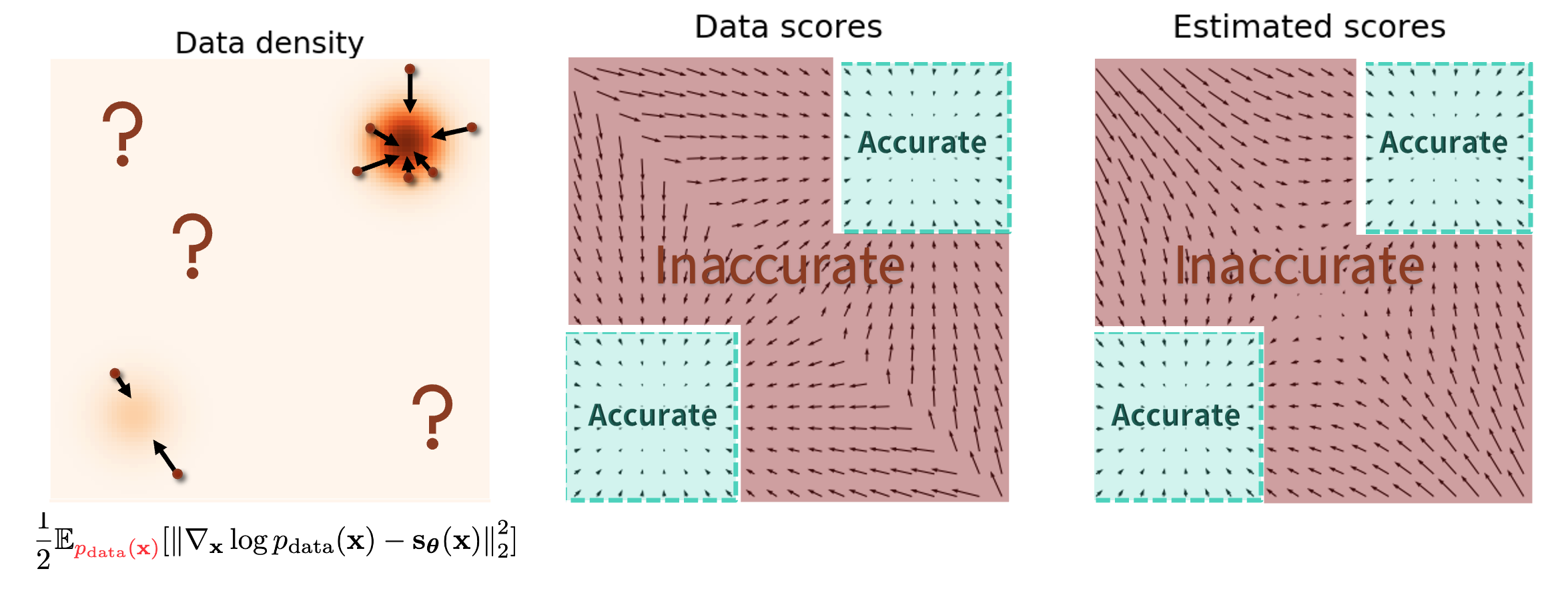
这一点比较好理解，我的理解就是在低密度数据区域，数据的分布很稀疏，梯度方向不稳定，很难收敛到高数据密度区域，造成采样失败

  • 混合密度分布的比例系数会消失

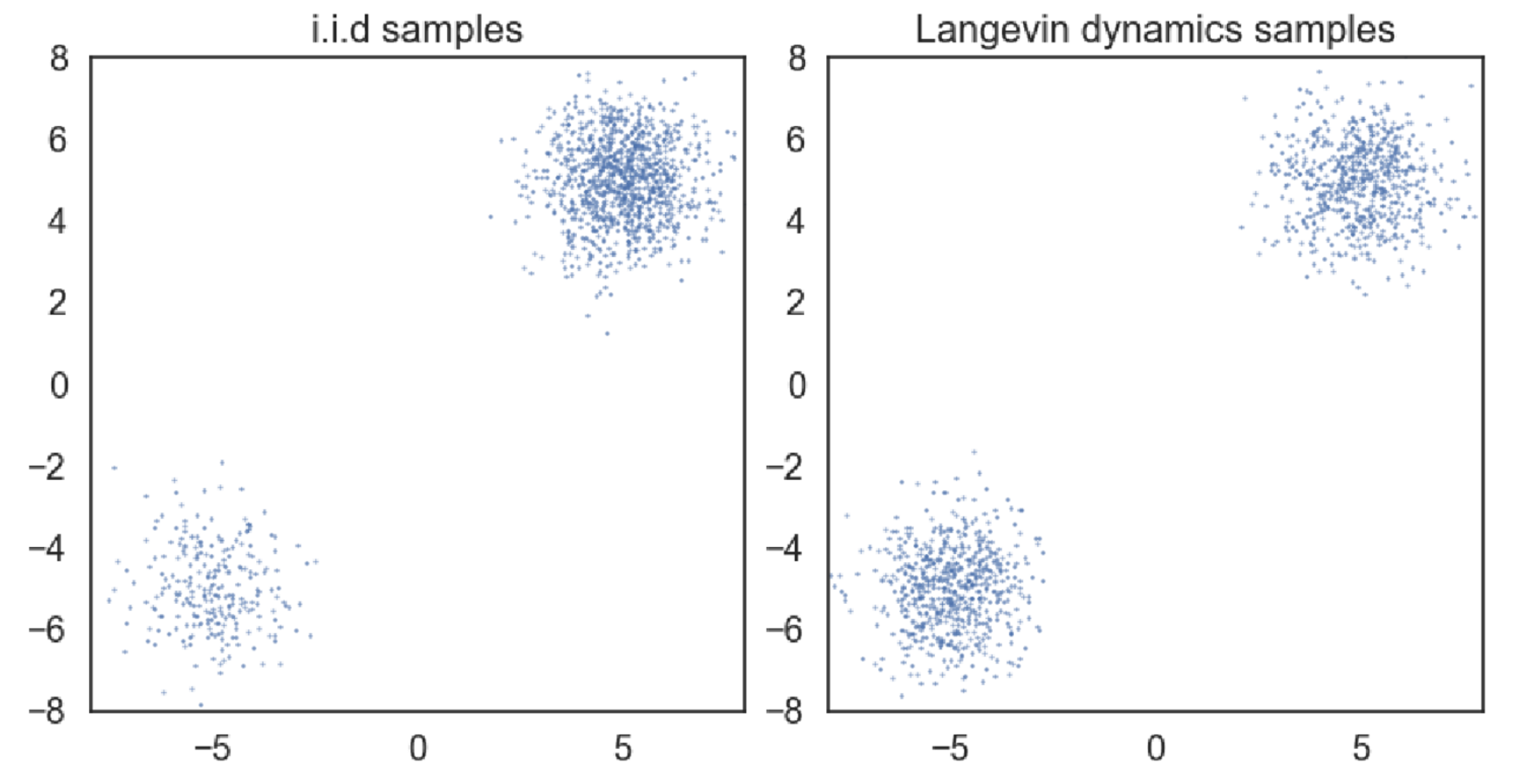
Gaussian Perturbation

通过Gaussian Perturbation，我们可以有效的解决上述问题：

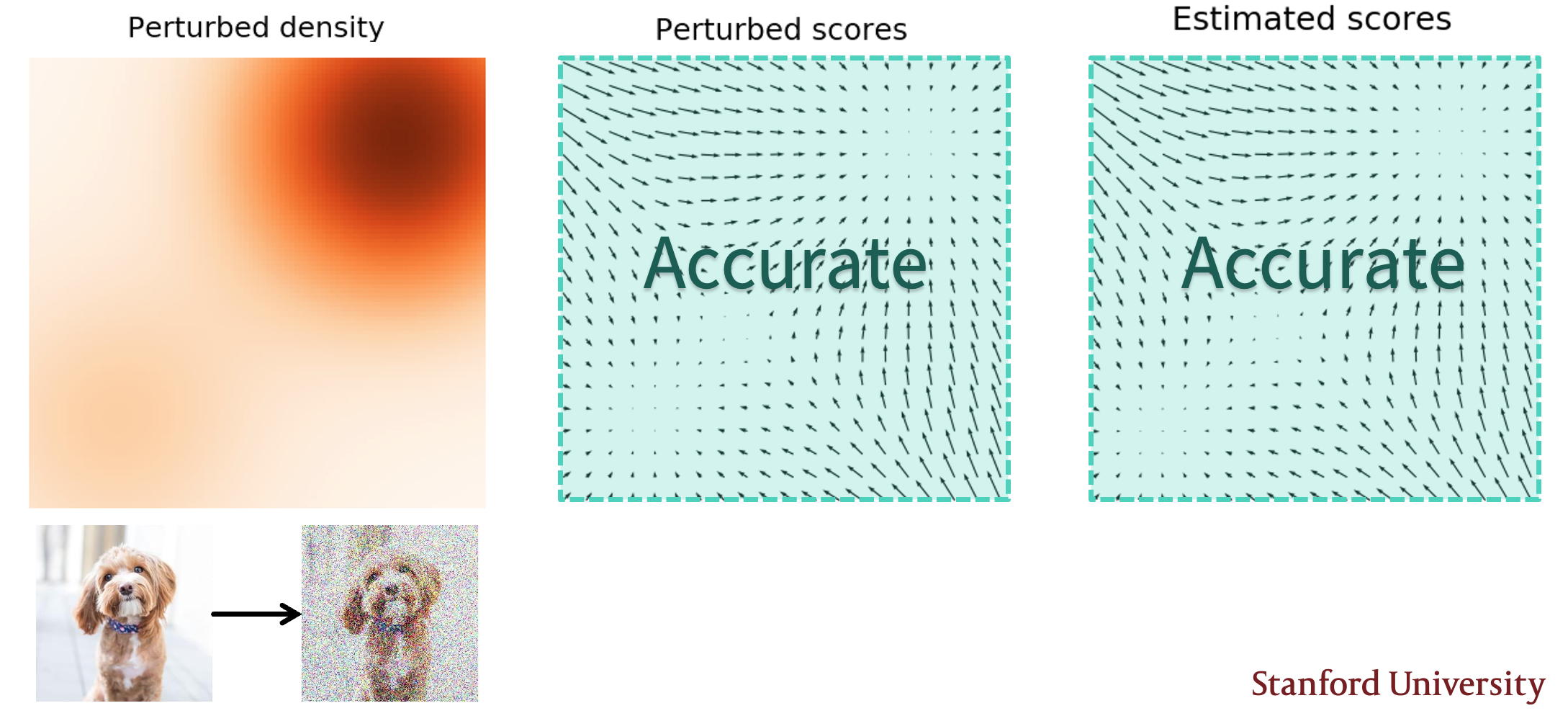
可以看到在加入Gaussian Perturbation后，低密度区域的数据密度得到提升，能够更好的计算score，进而提升了其在低密度区域的准确性。

Difference between denoising and Gaussian Perturbation

我在听stefano讲课的时候感觉同学们也没有完全get到他这里提到的perturbation和denoising SM的区别，我的理解是：

在这里的perturb和DSM其实是等价的，本质都是通过向数据加入噪声的一个处理，但是在DSM中，我们强调的是通过引入噪声来化简计算，而perturbation强调的是通过引入噪声来提升数据密度，进而提升score的准确性，这里提出的perturb是可以使用在任何score matching的算法中的，同时也为他在下文中引出的multi-noise perturbation做铺垫

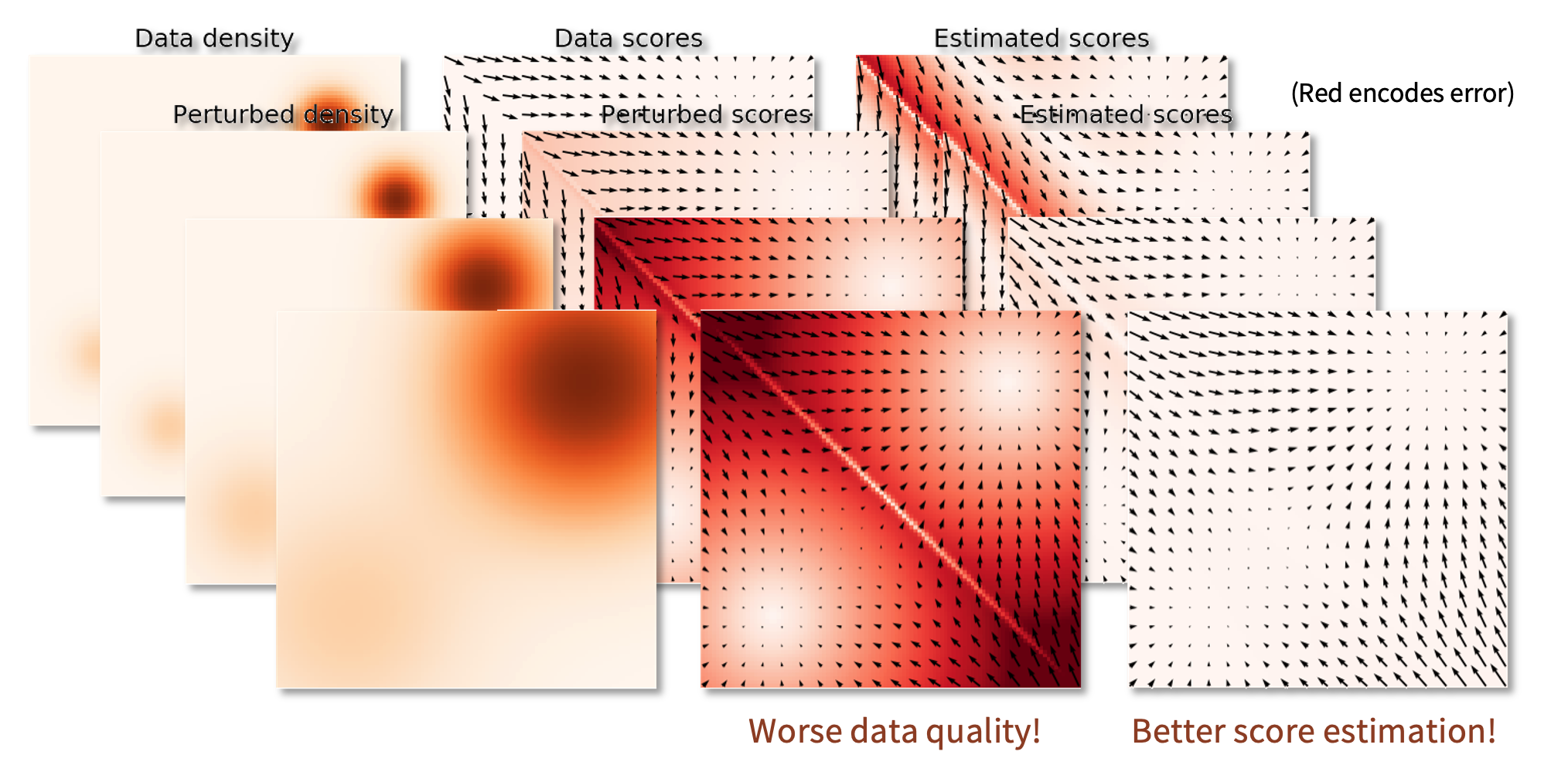
所以现在的问题来到了怎么添加noise，选择\(\sigma\)，因为：

  • 如果\(\sigma\)太小，那么数据分布的改变不会太大，那么score的估计也不会改变太多
  • 如果\(\sigma\)太大，那么数据分布的改变会太大，我们得到estimation与true data的差异会很大

trade off：

Multi-noise Perturbation

Understanding

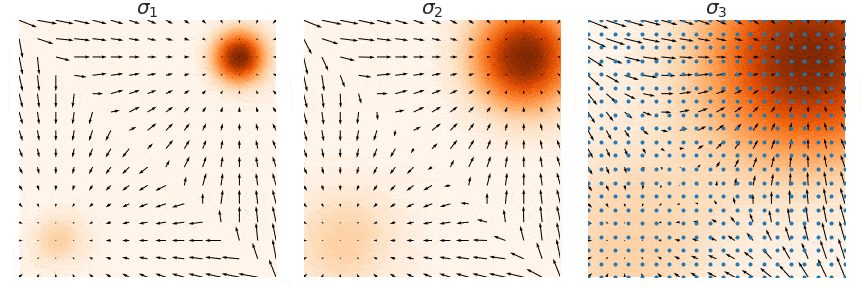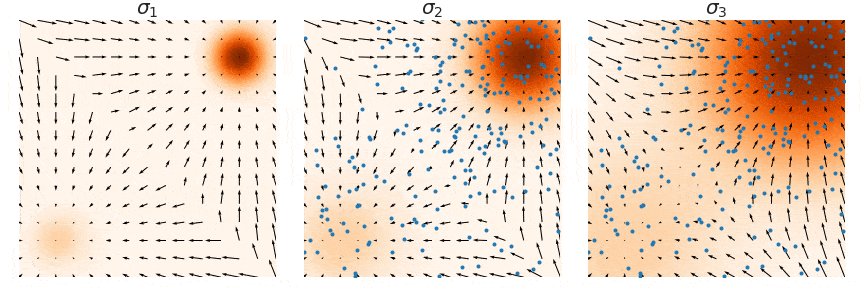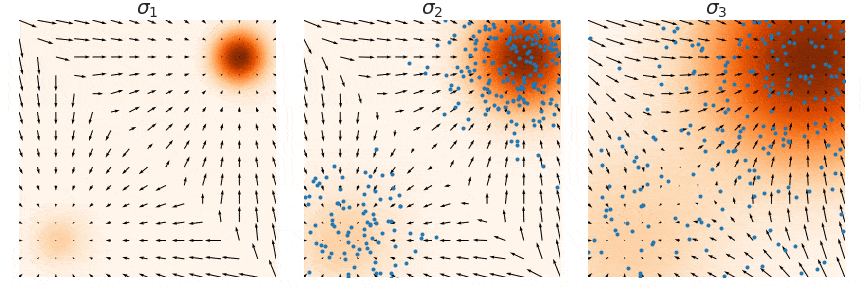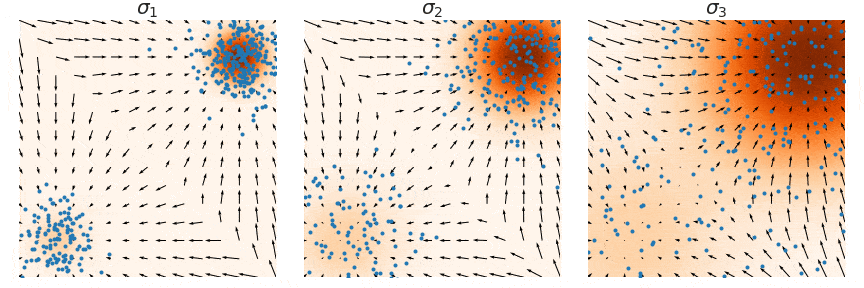
我们引入一种新的方法，尝试使用多个噪声进行加噪然后学习分数，原因用下面这张图来说明：

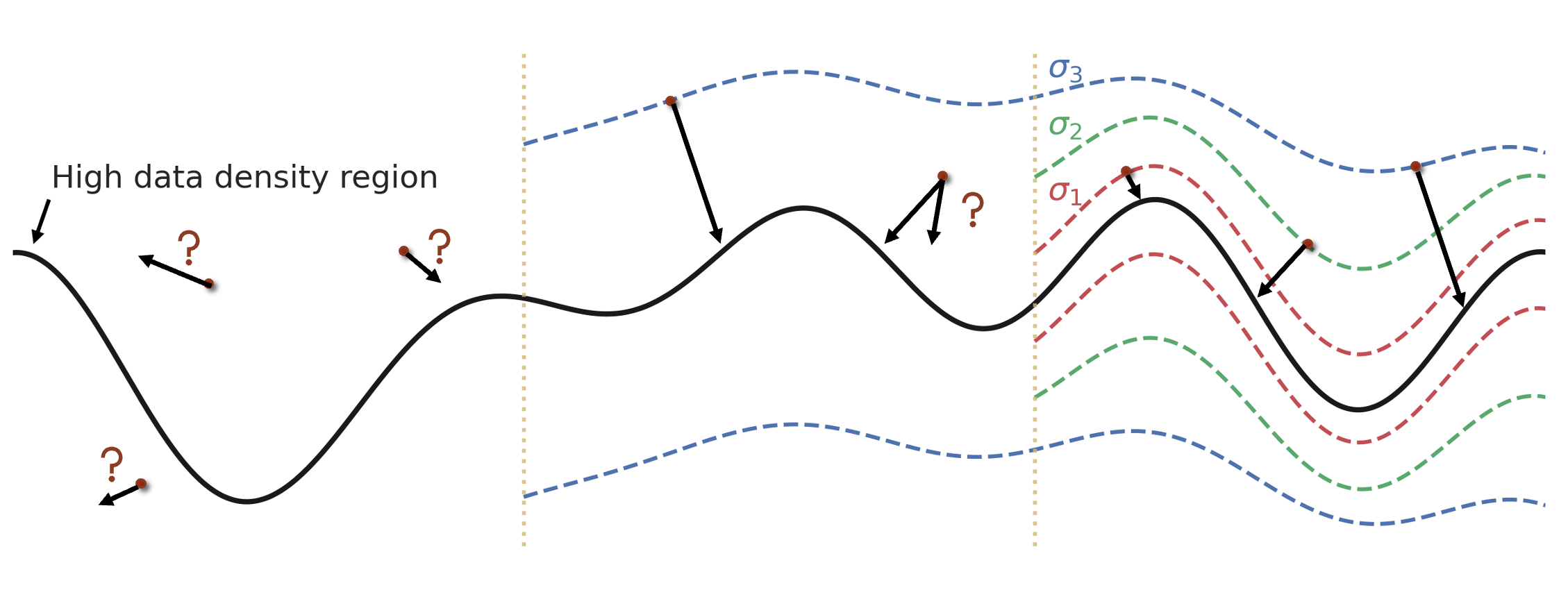
假设我们的数据落在这个黑色粗线附近，但是我们的采样可能会在这个平面中远离粗线的地方，这时较低的数据密度导致我们不能很好的估计梯度方向，使用不同的\(\sigma\)进行加噪，让我们的采样能够读到更好的梯度方向。

这就是score based model和diffusion model背后的思想，我们不仅要学习数据分布，不仅要学习数据分布加上单一噪声的分布，我们要学习数据被不同噪声量扰动后的分数

具体的实现如下：

  • Training:

    • simultaneously使用正交的高斯噪声\(\sigma_i\), \(\mathcal{N}(0, \sigma_i^2 I), i = 1, 2, \cdots, L\)进行加噪（加噪的方式是和DSM一样的）
    • 每次加噪后，计算score\(\nabla_{x} \log p_{\sigma_i}(x)\)，这一步是通过训练Noise Conditional Score Based Model \(\mathbf{s}_\theta(\mathbf{x}, i)\)来实现的

Noise Conditional Score Based Model

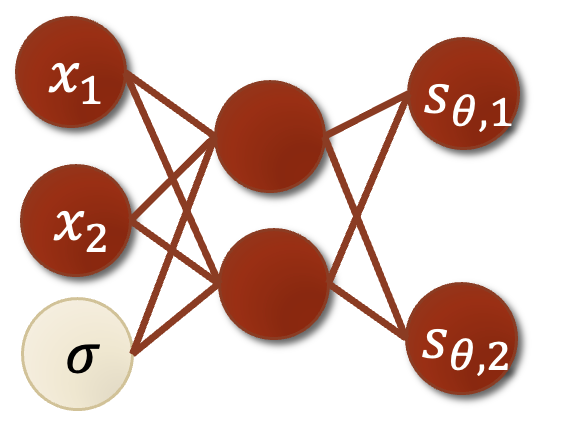
如果我们直接计算L个神经网络，将会十分expensive，所以我们这里使用一个神经网络，通过调整不同的\(\sigma_i\)来计算不同的score

这样就可以得到L个score，但是目标需要经过加权：

\[ \sum_{i=1}^{L} \lambda(i) \mathbb{E}_{p_{\sigma_i}(x)} [|| \left( \nabla_{x} \log p_{\sigma_i}(x) - \nabla_{x} \log p_{data}(x) \right) ||_{2}^2] \]
\[ \begin{aligned} & =\frac{1}{L} \sum_{i=1}^L \lambda\left(\sigma_i\right) E_{\mathbf{x} \sim p_{\mathrm{data}}, \mathbf{z} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})}\left[\left\|\nabla_{\tilde{\mathbf{x}}} \log q_{\sigma_i}(\tilde{\mathbf{x}} \mid \mathbf{x})-\mathbf{s}_\theta\left(\tilde{\mathbf{x}}, \sigma_i\right)\right\|_2^2\right]+\text { const. } \\ & =\frac{1}{L} \sum_{i=1}^L \lambda\left(\sigma_i\right) E_{\mathbf{x} \sim p_{\mathrm{data}}, \mathbf{z} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})}\left[\left\|\mathbf{s}_\theta\left(\mathbf{x}+\sigma_i \mathbf{z}, \sigma_i\right)+\frac{\mathbf{z}}{\sigma_i}\right\|_2^2\right]+\text { const. } \end{aligned} \]

这里的加权函数\(\lambda(i)\)通常等于\(\sigma_i^2\)

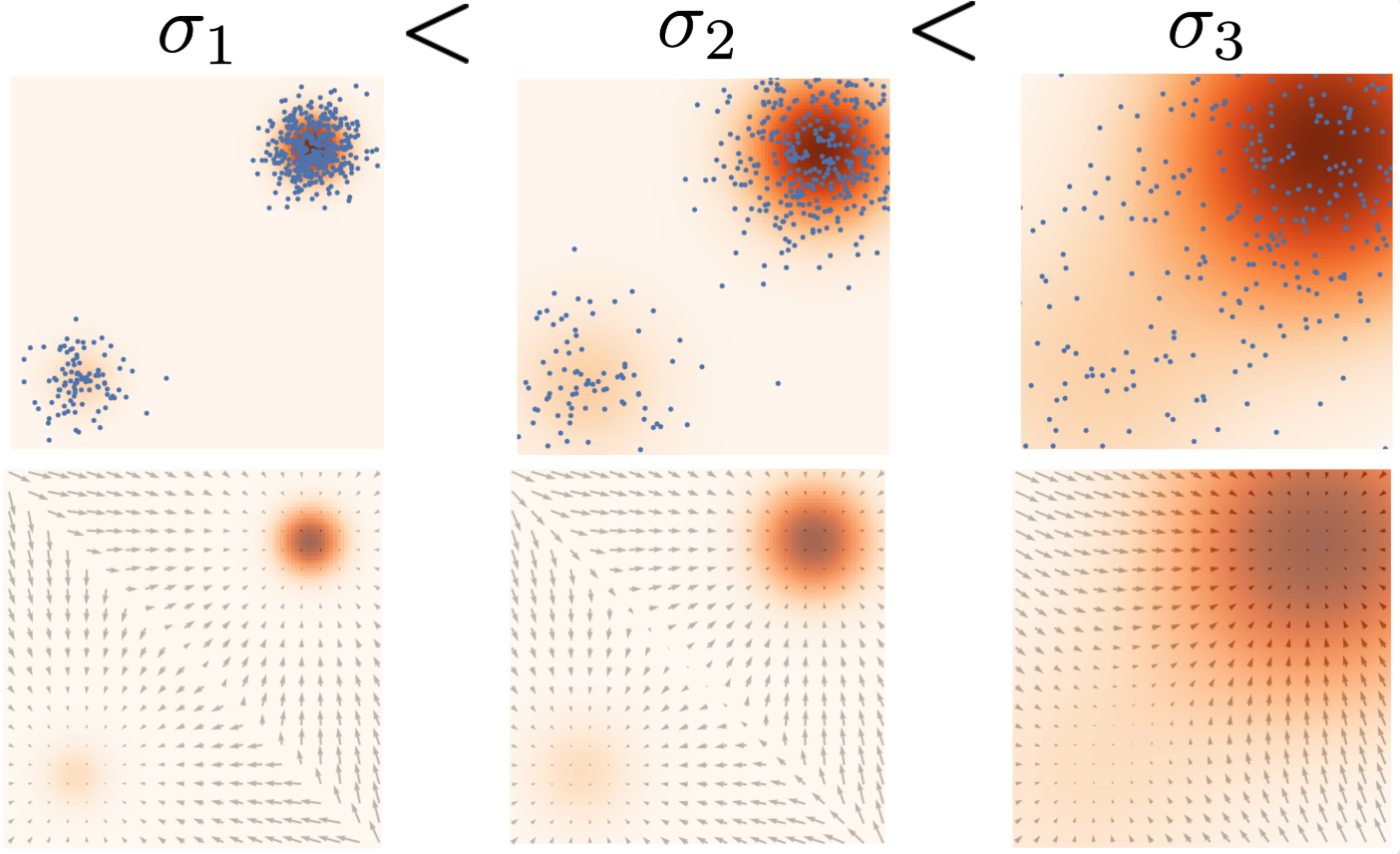
  • Sampling:

    • 使用Annealed Langevin dynamics for \(i = L, L-1, \cdots, 1\)进行采样

这个过程中使用退火朗之万，并且将每次的sample作为下一次的初始值

  • Noise Choice

最后还涉及到一些噪声的选择问题，我们知道噪声是一个递进的/递减的，所以这里涉及到这个噪声的变化过程：

key point是：

  • 相邻的噪声之间需要overlap to facilitate transitioning across noise scales
  • 采用geometry progression with sufficient length：
\[ \sigma_1 < \sigma_2 < \cdots < \sigma_L \]
\[ \frac{\sigma_i}{\sigma_{i+1}} = \text{constant} \]

Score-based models with SDEs

通过将noide level提升到 infinity, we obtain not only higher quality samples, but also, among others, exact log-likelihood computation, and controllable generation for inverse problem solving.

我们将上一步中的noise在时间维度取极限，得到一个连续的noise level，也就是一个随机微分方程（SDE）

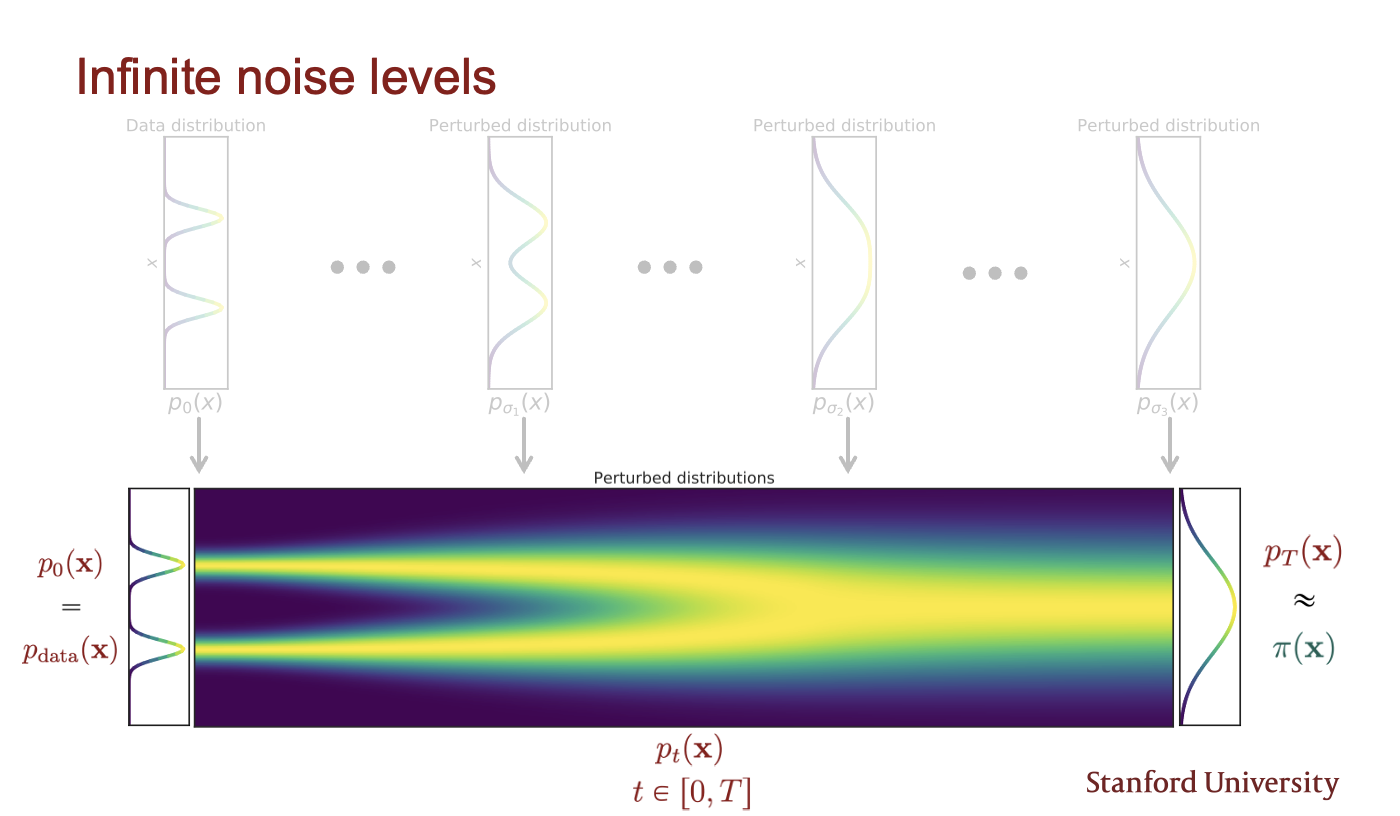
这样得到的就是一个完全的噪声：

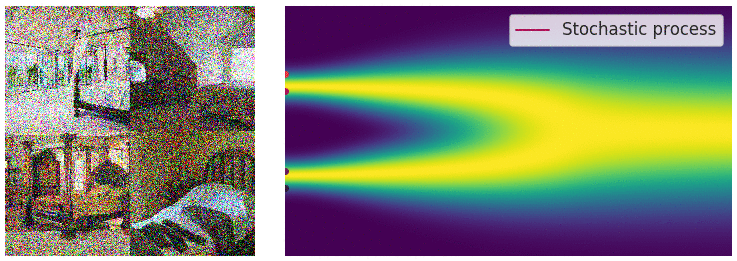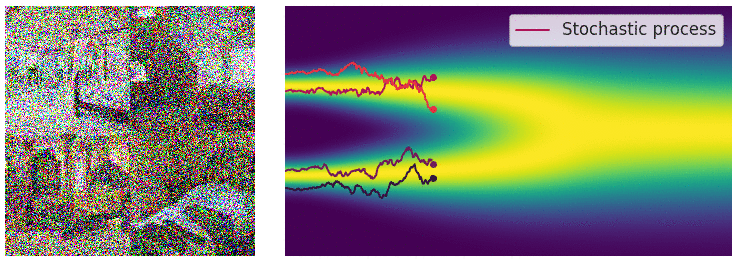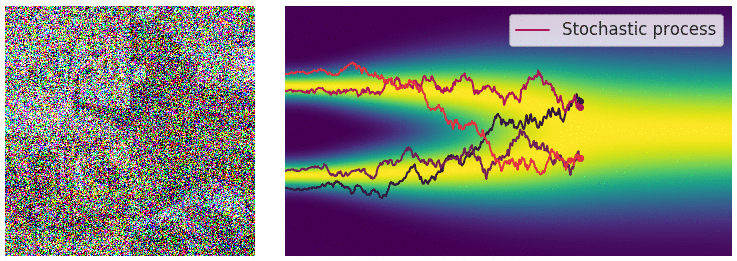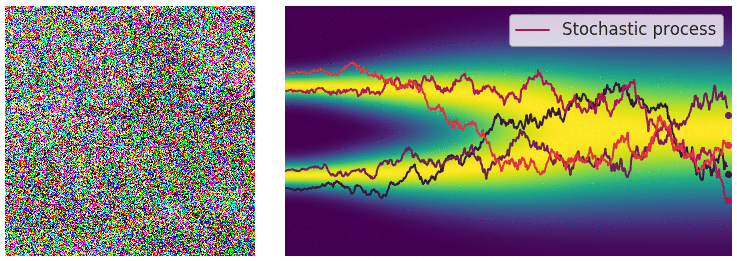
现在我们用SDE来表示这个过程：

\[ \mathrm{d} \mathbf{x} = \mathbf{f(\mathbf{x}, t)} \mathrm{d} t + \mathbf{g(t)} \mathrm{d} \mathbf{w} \]

Notation

  • \(f(x, t)\): drift coefficient，漂移系数决定数据的确定性演化方向
  • \(g(t)\): diffusion coefficient，扩散系数决定数据的随机性演化方向，控制噪声的强度
  • \(\mathbf{dw}\): Wiener process，标准布朗运动（维纳过程），表示无穷小的高斯白噪声

Choice of SDEs

噪声方差随时间增大，最终覆盖整个空间，快速爆炸噪声

\[ dx = \sqrt{\frac{d\sigma^2(t)}{dt}}dw, \text{ } \sigma(t) \rightarrow \infty, t\rightarrow T \]

总体方差保持稳定，常用于diffusion model

\[ \mathrm{d} \mathbf{x} = -\frac{1}{2} \beta(t) x \mathrm{d} t + \sqrt{\beta(t)} \mathrm{d} \mathbf{w} \]

这个随机微分方程的解是一个连续的随机变量集合\({x(t)}_{t \in [0, T]}\)，表示在时间\([0, T]\)内，数据\(x\)的演化过程（trace stochastic trajectory as t increases），这时我们的数据分布\(p_t(x)\)就是表示在时间\(t\)时，数据\(x(t)\)的marginal distribution density function，所以在\(t \rightarrow T\)时，\(p_t(x)\)就是噪声扰动后的数据分布\(\pi(x)\)

现在我们来考虑怎么进行sample，首先回顾我们的finite version，我们通过Annealed Langevin dynamics进行采样，即sequentially 在不同的噪声阶段进行朗之万动力学采样，现在我们将加噪过程变成了一个随机微分方程，那么自然的我们想求解这个SDE的reverse：

理论上每个SDE都有一个reverse SDE：

\[ \mathrm{d} \mathbf{x}=\left[\mathbf{f}(\mathbf{x}, t)-g^2(t) \nabla_{\mathbf{x}} \log p_t(\mathbf{x})\right] \mathrm{d} t+g(t) \mathrm{d} \mathbf{w} \]

不难发现，这里的\(\nabla_x log p_t(x)\)就是我们的score!

现在来看看训练思路：

根据上面的式子，不难观察出我们只需要知道：

  • terminal distribution \(p_T(x)\)：就是我们的加噪数据分布，tractable
  • score function \(\nabla_x \log p_t(x)\)：我们需要训练一个Time-Dependent Score-Based Model\(s_\theta(x, t)\)，such that \(\nabla_x \log p_t(x) \approx s_\theta(x, t)\)，这和我们对finite的训练是相似的: \(\nabla_x \log p_{\sigma_i}(x) \approx s_\theta(x, i)\)

这时我们的training obj就是：

\[ \mathbb{E}_{t \in \mathcal{U}(0, T)} \mathbb{E}_{p_t(\mathbf{x})}\left[\lambda(t)\left\|\nabla_{\mathbf{x}} \log p_t(\mathbf{x})-\mathbf{s}_\theta(\mathbf{x}, t)\right\|_2^2\right] \]

这里，\(mathcal{U}\)表示0，T之间的均匀分布，\(\lambda\)还是那个正项权重函数，通常选择\(\lambda(t) \propto \frac{1}{\mathbb{E}[\|\nabla_{\mathbf{x}(t)} \log p(\mathbf{x}(t) \mid \mathbf{x}(0))\|^2_2]}\)来对不同时间的score进行平衡。

这时对score function进行训练，用sliced或者denoising sm优化后，将结果插入SDE：

\[d\mathbf{x} = [\mathbf{f}(\mathbf{x}, t) - g^2(t)\mathbf{s}_{\theta}(\mathbf{x}, t)]dt + g(t)d\mathbf{w}\]

从\(x(T) \sim \pi\)开始，我们开始进行reverse SDE解，得到\(x(0)\)，当score well-trained时，这时的\(x(0)\)就是一个approximate sample from distribution \(p_0\)

likelihood weighting function

在这里我们可以引入likelihood，通过选择一个weighting function \(\lambda(t) = g^2(t)\)使得

\[\text{KL}(p_0(\mathbf{x}) \| p_{\theta}(\mathbf{x})) \leq \frac{T}{2}\mathbb{E}_{t \in \mathcal{U}(0,T)}\mathbb{E}_{p_t(\mathbf{x})}[\lambda(t)\|\nabla_{\mathbf{x}} \log p_t(\mathbf{x}) - \mathbf{s}_{\theta}(\mathbf{x}, t)\|^2_2] + KL(p_T || \pi)\]

由于这个式子中带有的KL散度，并且最小化KL散度和最大化模型训练中的似然是等价的，我们给这个加权函数才起名为似然加权函数，并且Yang Song的博客中提到这个追求似然的训练结果会比当时最好的AR模型更好

Predictor-Corrector

首先看怎么解SDE：

  • Euler-Maruyama method: 采用离散化SDE，用finite step来逐渐逼近SDE的解，这个过程很像朗之万动力学，都是在逐渐逼近目标分布的同时加入扰动
\[\Delta\mathbf{x} \leftarrow [\mathbf{f}(\mathbf{x}, t) - g^2(t)\mathbf{s}_{\theta}(\mathbf{x}, t)]\Delta t + g(t)\sqrt{|\Delta t|}\mathbf{z}_t, \text{ } \mathbf{z}_t \sim \mathcal{N}(0, \mathbf{I})\]
\[\mathbf{x} \leftarrow \mathbf{x} + \Delta\mathbf{x}\]
\[t \leftarrow t + \Delta t\]

  • Predictor：

    使用任何一种numerical method that predicts \(x(t + \Delta t) \sim p_{t+\Delta t}(x)\) from existing sample \(x(t)\sim p_t(x)\)

  • Corrector：

    任何独立依赖score function的MCMC procedure，例如朗之万或者是汉密尔顿MC

使用中就是先用predictor预测，再用corrector纠正

Controllable generation

关于加入限定条件的生成任务，也就是通过贝叶斯公式对概率进行条件约束，在这里score function是很合适做这个任务的，因为对贝叶斯公式：

假设我们知道正向生成结果\(p(y|x)\)

\[ p(\mathbf{x} \mid \mathbf{y}) = \frac{p(\mathbf{x}, \mathbf{y})}{p(\mathbf{y})} = \frac{p(\mathbf{y} \mid \mathbf{x})p(\mathbf{x})}{\int p(\mathbf{y} \mid \mathbf{x})p(\mathbf{x})d\mathbf{x}} \]

通过取梯度可以极大的化简这个式子：

\[ \nabla_x \log p(\mathbf{x} \mid \mathbf{y}) = \nabla_x \log p(\mathbf{y} \mid \mathbf{x}) + \nabla_x \log p(\mathbf{x}) \]

因为后两项分别是已知的和score function，所以先验概率很好得到了

以上内容在25 Summer 期末周前完成，coding部分如果有时间的话我也想好好看看的，但是临近期末，先不看了，后面有时间的话可以补上，但我还是倾向于将flow matching方向的理解先完成

留言

欢迎在下方交流~