Diffusion Models

约 2868 个字 8 张图片 预计阅读时间 10 分钟

Abstract

这一节的内容我先看了CS236的部分，Stefano对Diffusion的讲解主要建立在Score-based Models的基础上，这也是一种理解扩散模型的视角，然后我看了MIT的6.S184对于这部分的讲解。

Intro

回顾一下我们在Score-based Models中介绍的分数模型方法，我们定义一个分数来对数据分布进行评价，在denoising score matching中，通过加噪过程，得到一个易于采样的数据，再通过去噪过程，得到一个去噪后的数据，这个去噪后的数据就是我们的目标数据。

在Diffusion Models中，我们也做了类似的事情：

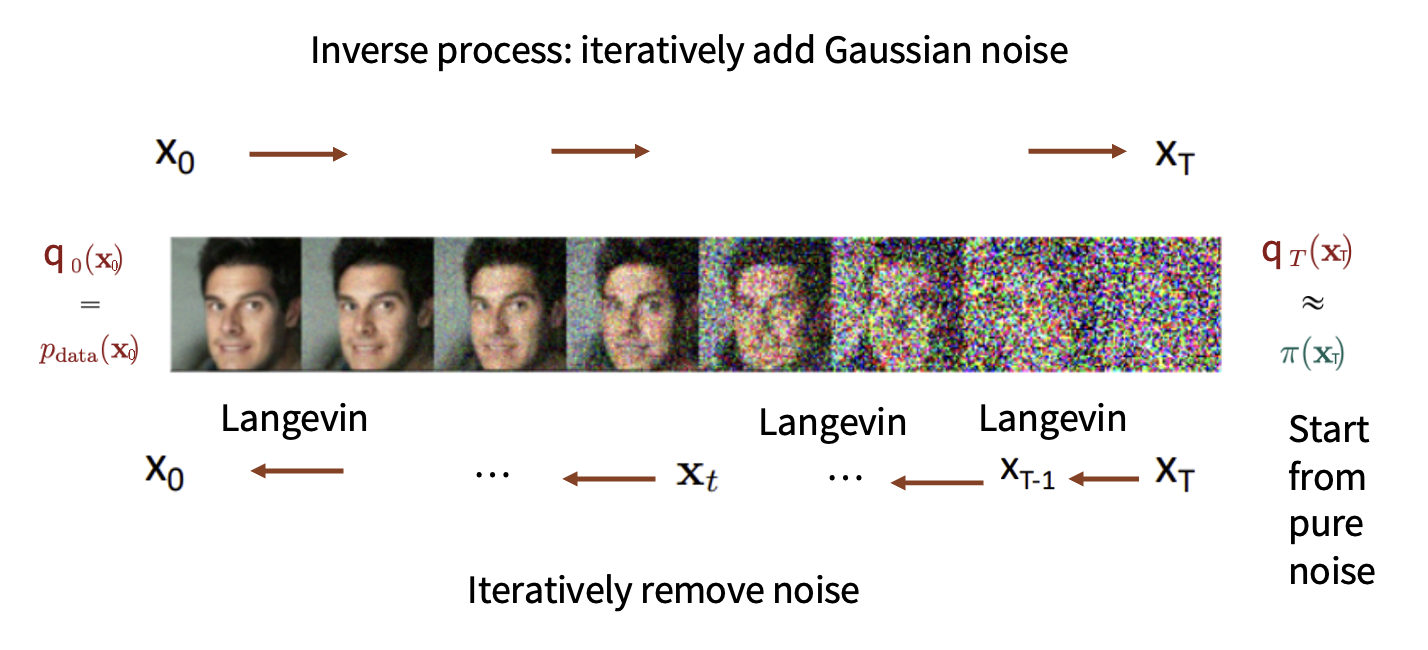
接下来的工作就是看如何重新定义这个马尔可夫过程的细节，具体到计算层面。

Noising Process

这里基本上与denoising score matching类似

\[ q(x_t|x_{t-1}) = \mathcal{N}(x_t; \sqrt{1-\beta_t}x_{t-1}, \beta_t\mathbf{I}) \]

同时这一步骤也可以采用multi-step的方式，即：

\[ q(x_t|x_0) = \mathcal{N}(x_t; \sqrt{\bar{\alpha}_t}x_0, (1-\bar{\alpha}_t)\mathbf{I}) \]

其中，\(\bar{\alpha}_t = \prod_{i=1}^t (1-\beta_i)\)。

Diffusion Process

按照思路进行下去，我们在逆向过程中只需要做 iteratively sample from \(q(x_{t-1}|x_t)\)，但问题是：

这个真实计算量非常大（用贝叶斯定理展开发现我们需要计算t-1和t时刻的边缘概率分布，这需要对前面的所有时刻进行积分）

我们的解决措施是学一个变分近似\(p_\theta(x_{t-1}|x_t)\)来对真实分布进行近似

为什么这样近似？

虽然\(q(x_{t-1}|x_t)\)是未知的，但通过数学推导我们可以证明，在给定了先验\(x_0\)的情况下，\(q(x_{t-1}|x_t, x_0)\)会变成一个可计算的高斯分布，他的方差和均值都可以用给定的\(\beta_t\)来得到

证明

卧槽好多公式

我们的目标是证明\(q(x_{t-1}|x_t, x_0)\)是一个高斯分布，并且他的方差和均值都可以用给定的\(\beta_t\)来得到

用贝叶斯展开这个式子：

\[ q(x_{t-1}|x_t, x_0) = \frac{q(x_t|x_{t-1}, x_0)q(x_{t-1}|x_0)}{q(x_t|x_0)} \]

由马尔可夫过程的性质，我们知道\(x_t\)只与\(x_{t-1}\)有关，与\(x_0\)无关，所以\(q(x_t|x_{t-1}, x_0) = q(x_t|x_{t-1})\)，同时\(q(x_t|x_0)\)与\(x_{t-1}\)无关，所以分母当作常数我们不看

这样此时目标正比于这两个部分：

\[ q(x_t|x_{t-1}) = \mathcal{N}(x_t; \sqrt{\alpha_{t}}x_{t-1}, (1-\alpha_{t})\mathbf{I}) \tag{1} \]

\[ q(x_{t-1}|x_0) = \mathcal{N}(x_{t-1}; \sqrt{\bar{\alpha}_{t-1}}x_0, (1-\bar{\alpha}_{t-1})\mathbf{I}) \tag{2} \]

因为一个正态分布的pdf的指数上满足：\(\exp(-\frac{(x-\mu)^2}{2\sigma^2}) = \exp(-\frac{x^2}{2\sigma^2} + \frac{x\mu}{\sigma^2} - \frac{\mu^2}{2\sigma^2})\)，所以我们知道只需要得到二次项和一次项系数，就可以知道这个分布的均值和方差

展开后我们得到指数部分为：

\[ -\frac{1}{2}\left(\left(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}_{t-1}}\right) \mathbf{x}_{t-1}^2-\left(\frac{2 \sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t+\frac{2 \sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}} \mathbf{x}_0\right) \mathbf{x}_{t-1}+C\left(\mathbf{x}_t, \mathbf{x}_0\right)\right) \]

所以此时我们能得到方差和均值：

\[ \begin{aligned} \tilde\beta_t &= \frac{(1-\bar{\alpha}_{t-1})(1-\alpha_t)}{1-\bar{\alpha}_t} \\ \tilde\mu_t &= \frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} \mathbf{x}_0 ; \text{ 这时可以代入} \mathbf{x}_0 = \frac{1}{\sqrt{\bar{\alpha}_{t}}} (\mathbf{x}_t - \sqrt{1-\bar{\alpha}_t}\epsilon_t) \\ &= \frac{1}{\sqrt{\alpha_t}} \left(\mathbf{x}_t + \frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon_t\right) \end{aligned} \]

成功证明：\(q(x_{t-1}|x_t, x_0) \sim \mathcal{N}(x_{t-1}; \tilde\mu_t, \tilde\beta_t\mathbf{I})\)

并且也可以显然看出，他们都是关于给定参数的可计算函数

所以这启发我们，我们只需要学习一个神经网络来近似\(\tilde\mu_t\)和\(\tilde\beta_t\)，就可以得到一个变分近似\(p_\theta(x_{t-1}|x_t)\)（在实际情况(比如DDPM)中，我们只需要学习\(\tilde\mu_t\)）：

\[ p_\theta(x_{t-1}|x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t, t), \sigma_t^2\mathbf{I}) \]

进而得到最终的joint distribution，也就是我们的结果：

\[ p_\theta(x_{0:T}) = p(x_T) \prod_{t=1}^T p_\theta(x_{t-1}|x_t) \]

课上Stefano说经过证明，如果我们做的是朗之万采样，这里的\(\mu_\theta\)甚至就是sm中的score（wtf?）原因之后会说到。

Training

到目前为止，我们已经得到了两个模块，encoder & decoder

现在我们需要讨论一下training的问题

如果只对Diffusion过程的一步进行观察，我们发现这一过程很像是VAE对隐变量解码的过程：

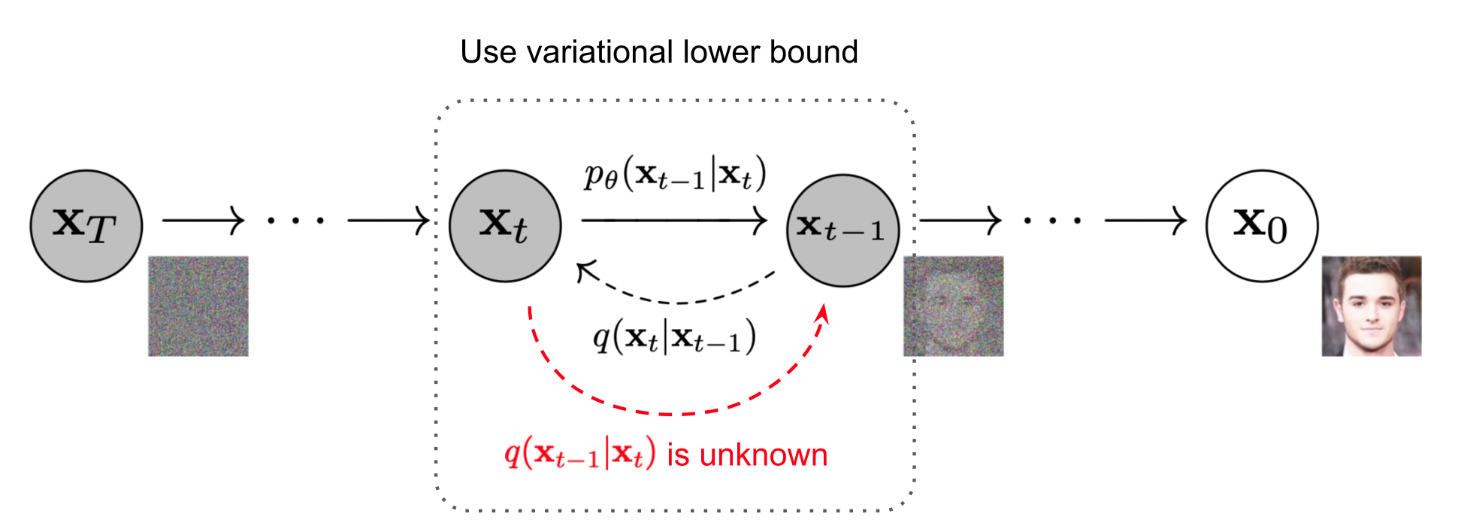
所以我们使用与ELBO类似的变分下界来进行训练

最原始的VAE loss是：

然后我们看增加latent层数后：

按照这个思路，我们可以得到层数为T的Diffusion Models的loss：

Loss of Diffusion Models

\[ \mathbb{E}_{q(\mathbf{x}_{0})}\left[-\log p_{\theta}(\mathbf{x}_{0})\right]\leq\mathbb{E}_{q(\mathbf{x}_{0})q(\mathbf{x}_{1:T}|\mathbf{x}_{0})}\left[-\log\frac{p_{\theta}(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})}\right]=:L \]

推导

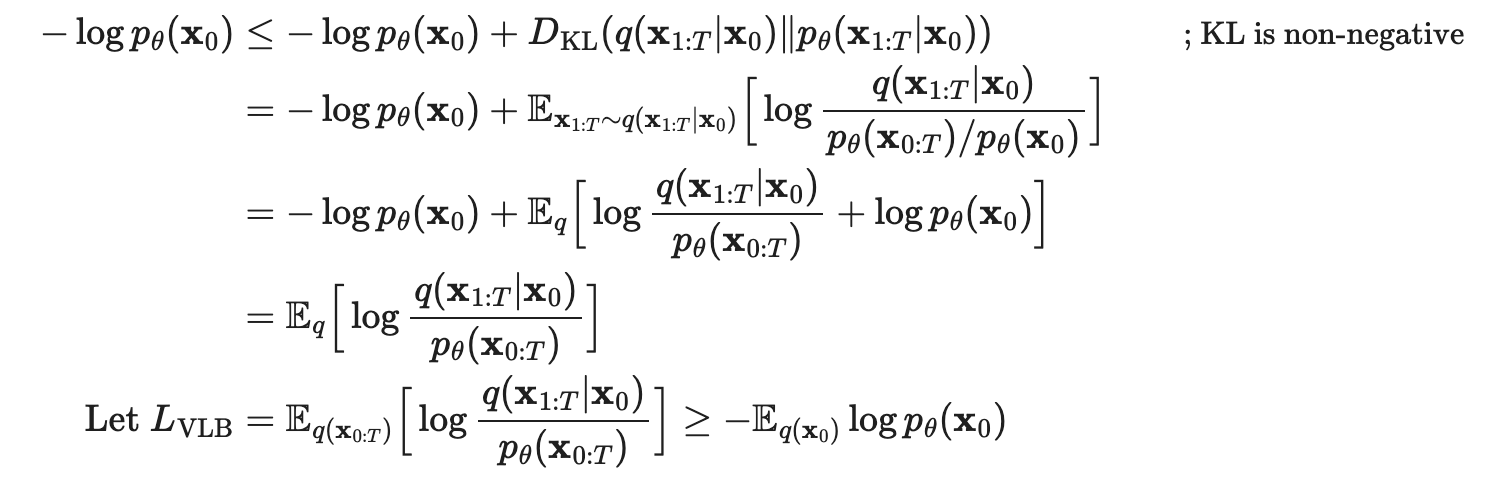
但是现在得到的这个loss是很难计算的，所以需要进行computable转换：

现在我们得到的这三种L中\(L_0\)是常量，而\(L_T\)中的\(x_T\)是已知的，我们忽略掉最后一项，将第一项设置为高斯分布

现在需要处理\(L_t\)，对其进行参数化：

• 对\(\mu_\theta\)进行参数化，因为在每一步我们是知道\(x_t\)的，所以就是对噪声\(\epsilon_t\)进行参数化，这时的Loss被参数化为minimize \(\mu_\theta\) 和 \(\tilde \mu_t\)，并最终化简为：

\[ L_t =\mathbb{E}_{\mathbf{x}_0,\mathbf{\epsilon}}{\left[\frac{(1-\alpha_t)^2}{2\alpha_t(1-\bar{\alpha}_t)\|\mathbf{\Sigma}_\theta\|_2^2}\|\mathbf{\epsilon}_t-\mathbf{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0+\sqrt{1-\bar{\alpha}_t}\mathbf{\epsilon}_t,t)\|^2\right]} \]

推导

这里lilian的博客中直接给出了带入近似的\(\mu_\theta\)的结果，我来稍微推导一下，主要是利用了KL在计算两个高斯分布时的性质，即：

\[ D_{KL}(P_{1}\mid\mid P_{2})=\frac{1}{2}\left[\log\frac{\det(\mathbf{\Sigma}_{2})}{\det(\mathbf{\Sigma}_{1})}-d+\mathrm{tr}(\mathbf{\Sigma}_{2}^{-1}\mathbf{\Sigma}_{1})+(\mathbf{\mu}_{2}-\mathbf{\mu}_{1})^{T}\mathbf{\Sigma}_{2}^{-1}(\mathbf{\mu}_{2}-\mathbf{\mu}_{1})\right] \]

其中d是维度，因为在DDPM中方差被固定不学习了，模型与真实分布方差相等后，上式就被简化：

\[ \begin{gathered}D_{KL}(q\mid\mid p_\theta)=\frac{1}{2}\left[0-d+d+(\mathbf{\mu}_\theta-\tilde{\mathbf{\mu}}_t)^T(\tilde{\beta}_t\mathbf{I})^{-1}(\mathbf{\mu}_\theta-\tilde{\mathbf{\mu}}_t)\right]\\=\frac{1}{2\tilde{\beta}_t}(\mathbf{\mu}_\theta-\tilde{\mathbf{\mu}}_t)^T(\mathbf{\mu}_\theta-\tilde{\mathbf{\mu}}_t)\\=\frac{1}{2\tilde{\beta}_t}\|\mathbf{\mu}_\theta(\mathbf{x}_t,t)-\tilde{\mathbf{\mu}}_t(\mathbf{x}_t,\mathbf{x}_0)\|^2\end{gathered} \]

这时我们再带入\(\mu_\theta\)和\(\tilde\mu_t\)即可

在实际的操作中，DDPM发现训练目标可以进行化简，放弃噪声距离前的那个权重，所以最终我们的loss被简化为：

\[ L_{\text{simple}} = \mathbb{E}_{t\sim[1,T],\mathbf{x}_0,\mathbf{\epsilon}_t}\left\lfloor\|\mathbf{\epsilon}_t-\mathbf{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0+\sqrt{1-\bar{\alpha}_t}\mathbf{\epsilon}_t,t)\|^2\right\rfloor \]

至此，我们就推导出了Diffusion Models原文算法中的各项内容：

Relation to Score Matching

我想Score-based Models的思路这里可以不再做重复了，我们来看一下核心的部分，也就是score function，为了对比，我在这里使用ddpm中的notation：

\[ \mathbf{s}_\theta(\mathbf{x}_t, t) \approx \nabla_{\mathbf{x}_t}\log q(\mathbf{x}_t) \]

由于我们使用的是高斯分布：

\[ \nabla_{\mathbf{x}}\log p(\mathbf{x})=\nabla_{\mathbf{x}}{\left(-\frac{1}{2\sigma^{2}}(\mathbf{x}-\mathbf{\mu})^{2}\right)}=-\frac{\mathbf{x}-\mathbf{\mu}}{\sigma^{2}}=-\frac{\mathbf{\epsilon}}{\sigma} \]

\[ \mathbf{s}_\theta(\mathbf{x}_t,t)\approx\nabla_{\mathbf{x}_t}\log q(\mathbf{x}_t)=\mathbb{E}_{q(\mathbf{x}_0)}[\nabla_{\mathbf{x}_t}\log q(\mathbf{x}_t|\mathbf{x}_0)]=\mathbb{E}_{q(\mathbf{x}_0)}{\left[-\frac{\mathbf{\epsilon}_\theta(\mathbf{x}_t,t)}{\sqrt{1-\bar{\alpha}_t}}\right]}=-\frac{\mathbf{\epsilon}_\theta(\mathbf{x}_t,t)}{\sqrt{1-\bar{\alpha}_t}} \]

推导过程(Gemini)

证明 \(\nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t) = \mathbb{E}_{q(\mathbf{x}_0|\mathbf{x}_t)}[\nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t|\mathbf{x}_0)]\)

1. 从左侧 (LHS) 出发

   我们从等式左侧的定义开始，应用对数求导法则 \(\nabla \log f(x) = \frac{\nabla f(x)}{f(x)}\)：

   \[\nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t) = \frac{\nabla_{\mathbf{x}_t} q(\mathbf{x}_t)}{q(\mathbf{x}_t)}\]

2. 展开边缘概率 \(q(\mathbf{x}_t)\)

   \(q(\mathbf{x}_t)\) 是带噪数据的边缘概率分布。它是通过将联合分布 \(q(\mathbf{x}_t, \mathbf{x}_0)\) 对所有可能的初始数据 \(\mathbf{x}_0\) 进行积分得到的。而联合分布可以写作 \(q(\mathbf{x}_t, \mathbf{x}_0) = q(\mathbf{x}_t|\mathbf{x}_0)p_{data}(\mathbf{x}_0)\)。

   \[q(\mathbf{x}_t) = \int q(\mathbf{x}_t|\mathbf{x}_0) p_{data}(\mathbf{x}_0) d\mathbf{x}_0\]

   现在我们对它求梯度。梯度算子 \(\nabla_{\mathbf{x}_t}\) 可以移动到积分号内部（在满足一定正则性条件下，此处成立）：

   \[\nabla_{\mathbf{x}_t} q(\mathbf{x}_t) = \int \nabla_{\mathbf{x}_t} q(\mathbf{x}_t|\mathbf{x}_0) p_{data}(\mathbf{x}_0) d\mathbf{x}_0\]

3. 再次使用对数求导法则（逆向）

   注意到 \(\nabla f(x) = f(x) \nabla \log f(x)\)，我们可以将这个技巧应用到积分号内部的项 \(\nabla_{\mathbf{x}_t} q(\mathbf{x}_t|\mathbf{x}_0)\) 上：

   \[\nabla_{\mathbf{x}_t} q(\mathbf{x}_t|\mathbf{x}_0) = q(\mathbf{x}_t|\mathbf{x}_0) \nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t|\mathbf{x}_0)\]

   将这个结果代回到第2步的梯度表达式中：

   \[\nabla_{\mathbf{x}_t} q(\mathbf{x}_t) = \int q(\mathbf{x}_t|\mathbf{x}_0) \nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t|\mathbf{x}_0) p_{data}(\mathbf{x}_0) d\mathbf{x}_0\]

4. 识别出期望的形式

   现在我们把第3步的结果代回到第1步的LHS表达式中：

   \[\nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t) = \frac{\int q(\mathbf{x}_t|\mathbf{x}_0) \nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t|\mathbf{x}_0) p_{data}(\mathbf{x}_0) d\mathbf{x}_0}{q(\mathbf{x}_t)}\]

   现在，我们对分子中的 \(q(\mathbf{x}_t|\mathbf{x}_0) p_{data}(\mathbf{x}_0)\) 应用贝叶斯定理，它等于 \(q(\mathbf{x}_0|\mathbf{x}_t)q(\mathbf{x}_t)\)：

   \[\nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t) = \frac{\int \nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t|\mathbf{x}_0) \cdot q(\mathbf{x}_0|\mathbf{x}_t) q(\mathbf{x}_t) d\mathbf{x}_0}{q(\mathbf{x}_t)}\]

   由于积分是关于 \(\mathbf{x}_0\) 的，\(q(\mathbf{x}_t)\) 可以被看作常数从积分中提出来：

   \[\nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t) = \frac{q(\mathbf{x}_t) \int \nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t|\mathbf{x}_0) q(\mathbf{x}_0|\mathbf{x}_t) d\mathbf{x}_0}{q(\mathbf{x}_t)}\]

   上下消去 \(q(\mathbf{x}_t)\)：

   \[\nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t) = \int \nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t|\mathbf{x}_0) q(\mathbf{x}_0|\mathbf{x}_t) d\mathbf{x}_0\]

   这个最后的积分形式，正是期望的定义。它表示的是函数 \(\nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t|\mathbf{x}_0)\) 在概率分布 \(q(\mathbf{x}_0|\mathbf{x}_t)\) 下的期望值。所以：

   \[\nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t) = \mathbb{E}_{q(\mathbf{x}_0|\mathbf{x}_t)}[\nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t|\mathbf{x}_0)]\]

   至此，我们证明了等式成立。

可以看到score所在的位置就是sampling中\(x_t\)的更新方向

Conditional Diffusion Models

Efficient Diffusion Models

留言

欢迎在下方交流~