跳转至

Autoregressive Model

约 1245 个字 17 张图片 预计阅读时间 4 分钟

Abstract

自回归模型是使用非常广泛的一种生成模型，在先前的粗略学习中我大概知道了部分架构如CNN、RNN、Attention等，但是没有细致的了解过，这一部分会参考MIT那份教材多一些

Conditional Distribution Modeling

条件分布建模并不只适用于autoregressive model

在先前的学习中我们使用多个独立随机变量分布来建模，但是在实际生活中其实很多分布是相互依赖的

在先前的学习中（VAE），我们是利用独立的潜变量进行建模，但是这需要strict assumption for high-dimensional data（eg., 32x32x3 pixels）但是这很难：

所以我们引入另一种方式：采用条件分布建模

Chain Rule在这里被应用：

任何一个联合分布都能被写成条件分布的乘积：

\[ p(A, B, C) = p(A)p(B|A)p(C|A, B) \]

并且是

  • 任意排列的：
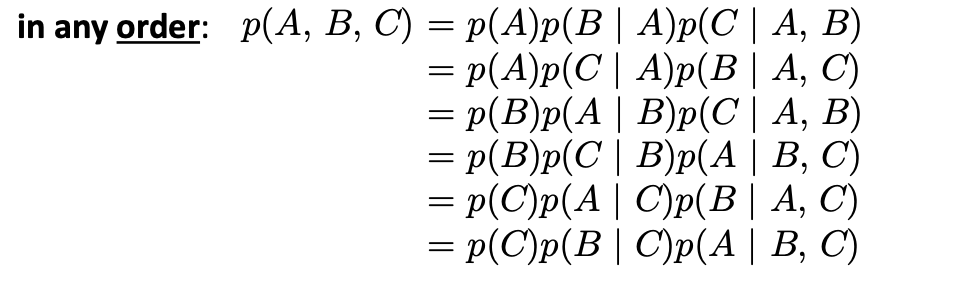
  • 任意分解的：

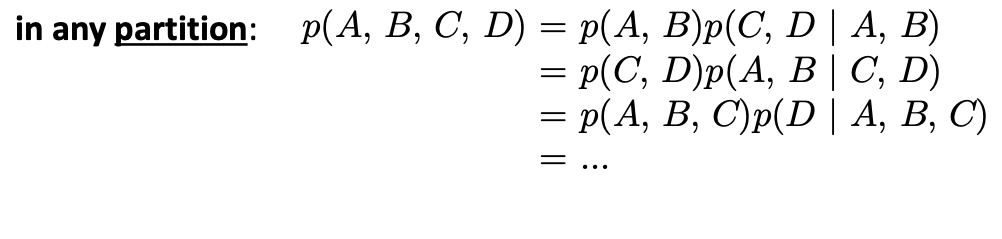
Case Study

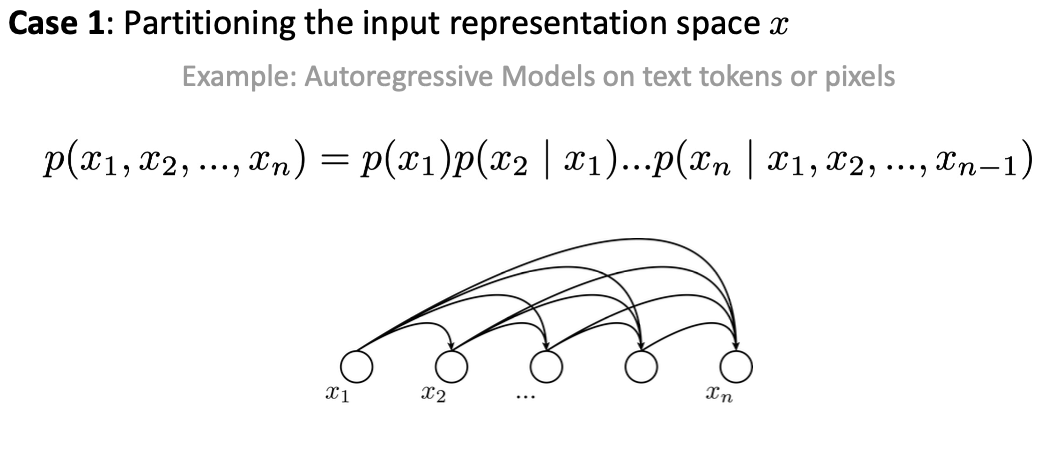
这适用于每个output依赖之前所有的output，如language model或者pixel prediction

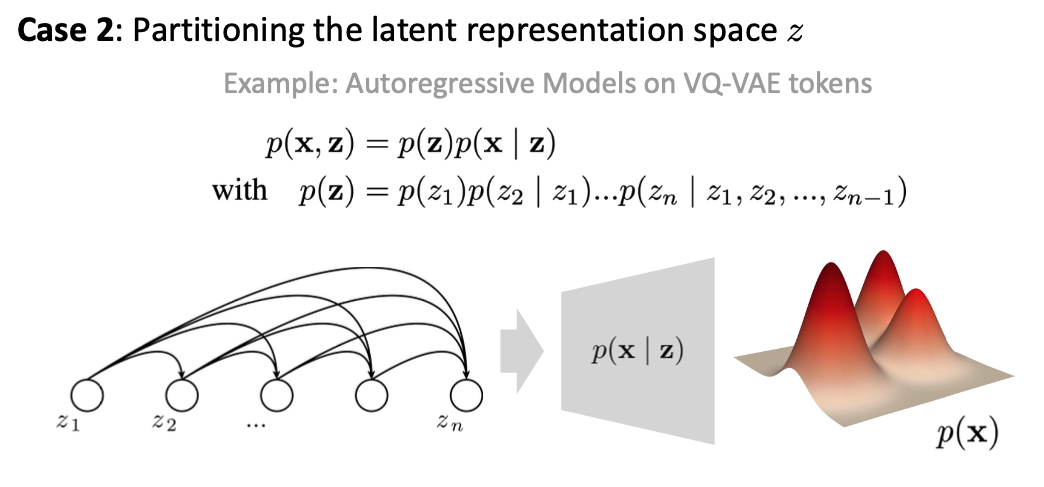
模型将noisy images(\(x_T\))转变为clean images(\(x_0\))的过程是diffusion process

在对联合分布进行建模时：我们使用神经网络对条件分布进行建模

\[ p(A, B, C) = p_{\theta}(A)p_{\phi}(B|A)p_{\psi}(C|A, B) \]
  • 理论上来说每个p拥有自己的weight，如果使用weight sharing则意味着inductive bias

Autoregression

Auto：self

  • using its own outputs for next prediction

Regression：

  • estimating relationship between variables

Note

  • 自回归是指在推理过程中的行为(inference-time)

  • 但是训练时(training-time)不一定是自回归的(eg., teacher-forcing就采用真实目标输出作为输入以加速训练，没有表现自回归特性)

In General：

\[ \begin{align} p(x_1, x_2, \cdots, x_n) &= p(x_1)p(x_2|x_1)p(x_3|x_1, x_2) \cdots p(x_n|x_1, x_2, \cdots, x_{n-1}) \\ &= \prod_{i=1}^{n} p(x_i|x_1, x_2, \cdots, x_{i-1}) \end{align} \]

  • \(x\) can be any representation:

    并不要求是序列的或者时间相关的(sequencial/temporal)

    例如任意维数的向量

  • \(x\) can be any order or partition

    order：\(x_n\) 到 \(x_1\) 也是一种合法的生成顺序

    partition：每个x都可以是标量、向量、张量

  • \(p(\dot|\dot)\) can take any form

    可以是各种形式的数据结构，离散连续都是支持的

Inductive Bias

在使用Chain Rule时，我们的公式是不涉及近似的，是一个完全准确的表达形式，但是这会导致模型参数爆炸💥，所以我们需要考虑到一些归纳偏置

通常来说每个p都是不同的映射，但我们引入shared architecture(RNN, CNN, Transformer)和shared weight \(\theta\)后就出现了approximation

Inference of AR

在原始Chain Rule中，我们可以得到这样的推理过程：

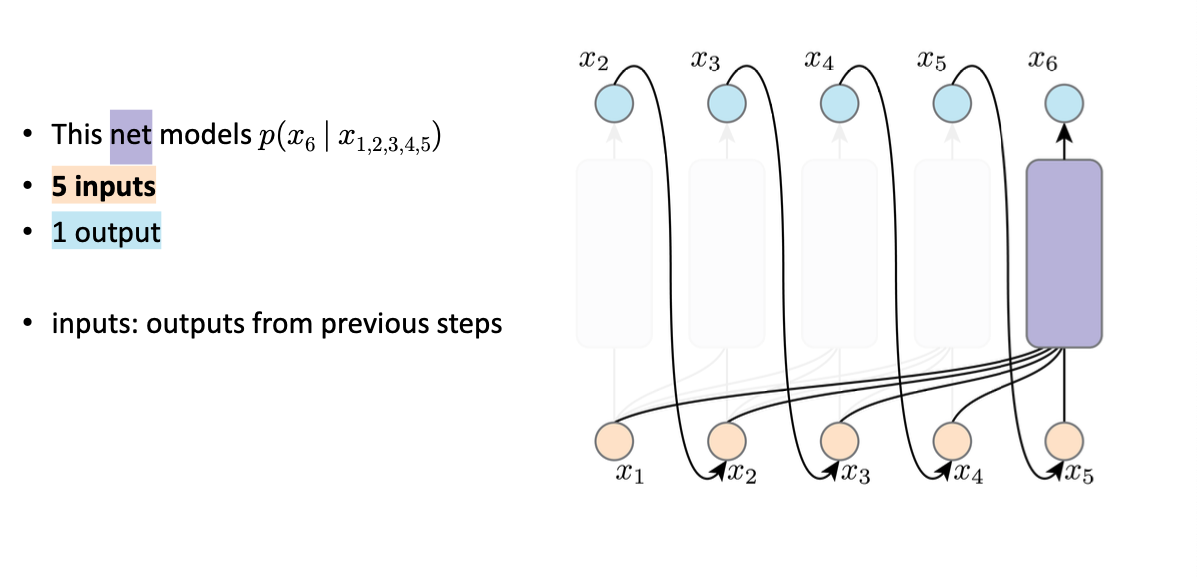
如果我们直接bp这个过程：

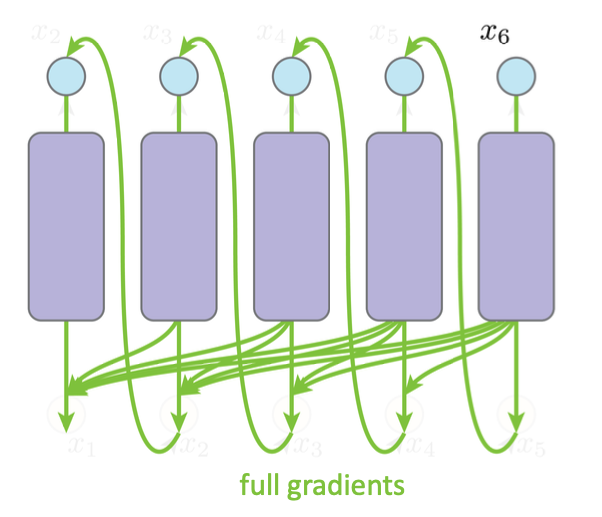
这条路径会走遍所有先前所有的outputs，所有的sampling operation和所有的networks

因此是infeasible❌ to train a AR following its inference graph

Training

我们采用teacher-forcing的方式进行训练，就是不考虑先前的输出结果，直接使用ground truth data

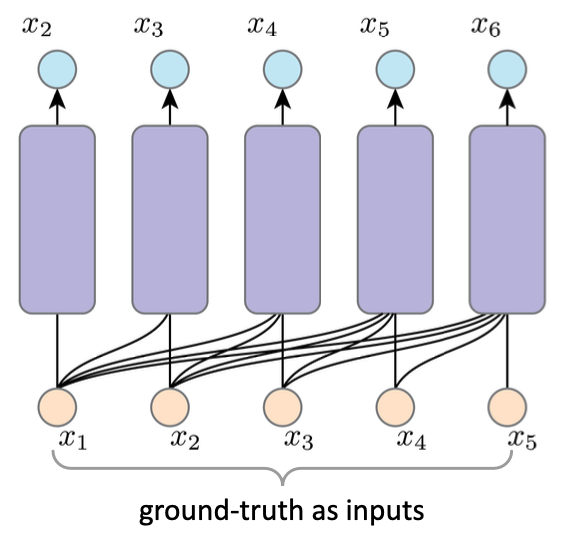
  • Pros：

    • bp路径短得多
    • ground truth inputs can ease training

  • Cons：

    • inconsistent：在训练与推理时不一致，因为在推理时没有ground truth来校正错误
    • distribution shift：不能看见自己的错误

Network Architecture

Autoregression is not architecture-specific❗️

先前我们讨论的东西都不涉及具体的架构，现在我们讨论一下具体的架构

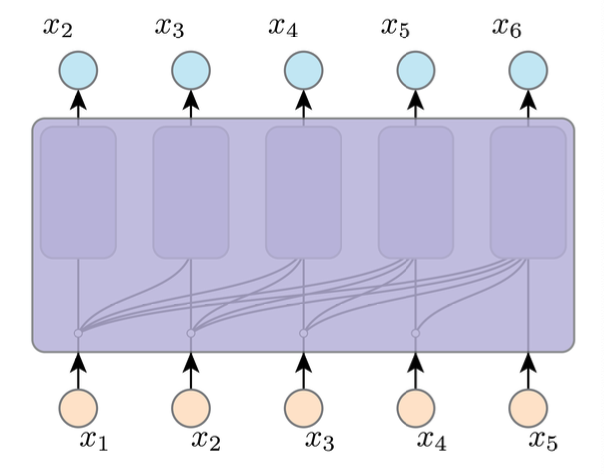
Shared Computation

之前我们说可以使用shared arch、weight，现在我们对神经网络层进行share

如果对每个\(j \geq i\)，output \(x_i\) not depend on \(x_j\)(就是输出只依赖之前而不依赖之后)

RNN

Recurrent Neural Network

构建一个RNN的步骤可以这样表示：

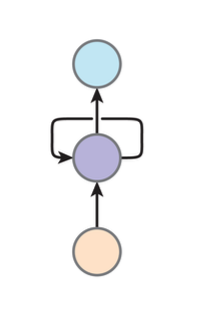
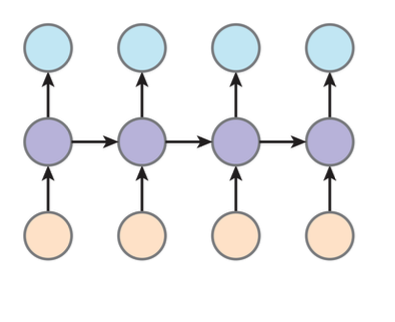
RNN可以理解为：keep a summary and recursively update it

在这里hidden layer \(h_i\)就是那个summary

我们进行更新的过程就是：

\[ h_{t+1} = \sigma(W_{hh}h_t + W_{xh}x_{t+1}) \]

然后进行预测：

\[ o_{t+1} = W_{hy}h_{t+1} \]

但是要注意我们的summary是需要进行初始化的\(h_0 = b_0\)

最终我们对三个矩阵进行训练，这三个矩阵的参数关于n是常数的

Example

Character RNN(Andrej Karpathy)

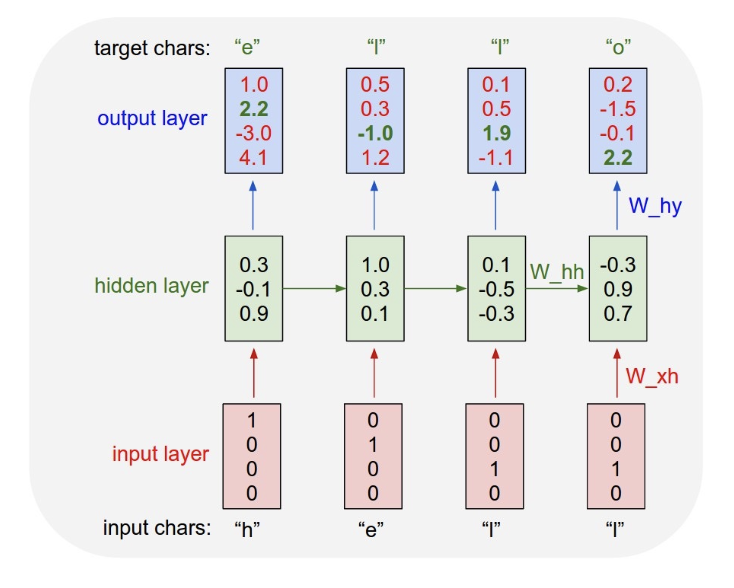
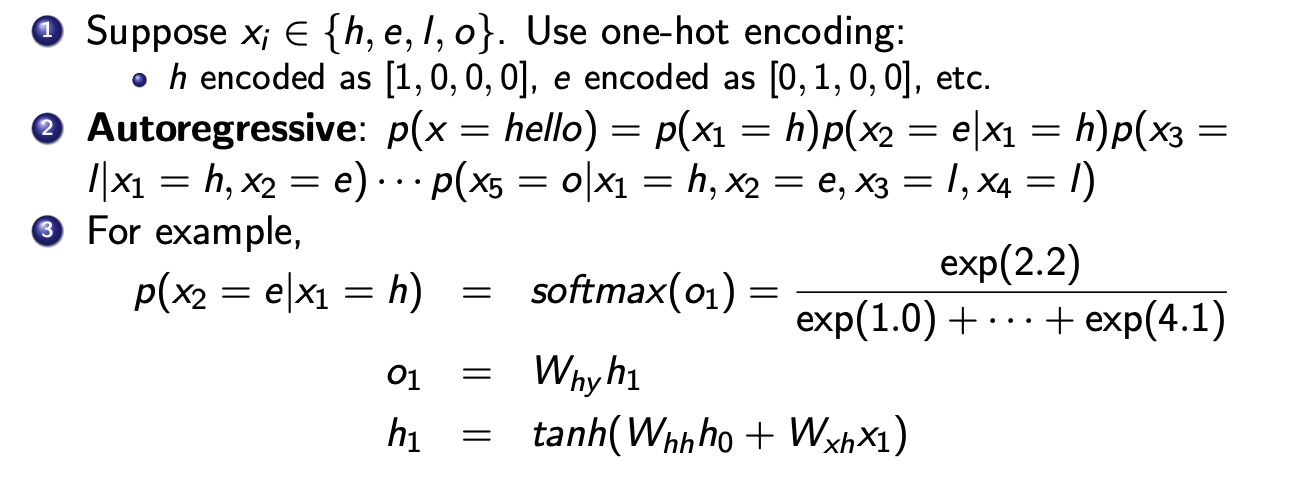
  • Pros:

    • 对任意长度都适用
    • 通用性：对任意computable function都存在一个finite RNN

  • Cons:

    • 需要排序
    • Sequencial likelihood evaluation 训练时很慢（因为无法并行计算）
    • 生成时是序列生成
    • 对长序列会有梯度消失/爆炸问题

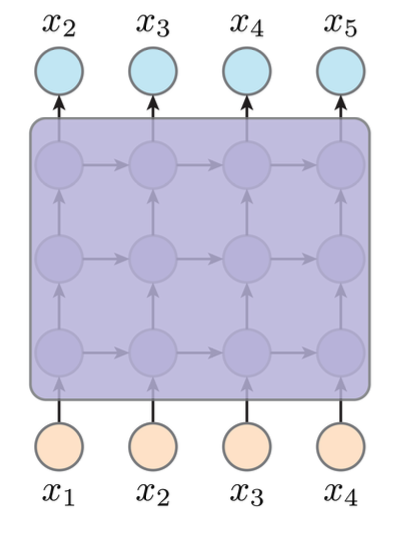
CNN

Convolutional Neural Network

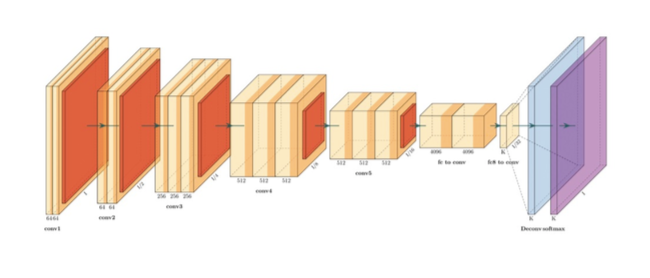
卷积神经网络依赖的是每个“像素”的局部性，也就是他们与周边空间的相互依赖关系，我的理解是卷积操作就是对原始数据进行down sampling的过程，让数据中蕴含的依赖关系更加明显，这其中采用的各类操作如卷积、池化、激活函数等都是为了这个目的。

在AR中，我们这样构建

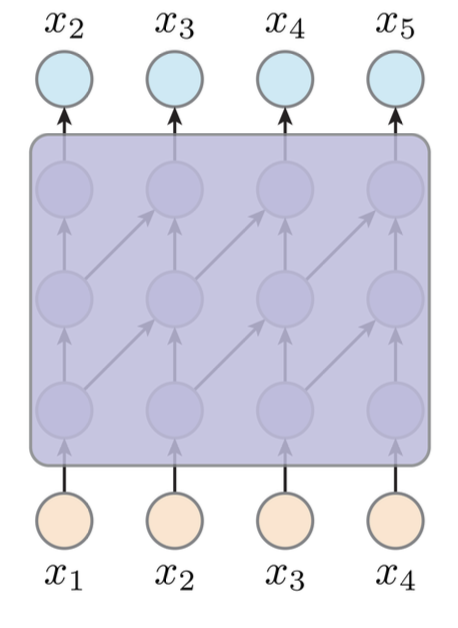
Attention

留言

欢迎在下方交流~