Normalizing Flow Models¶
约 2154 个字 30 行代码 7 张图片 预计阅读时间 8 分钟
在进行VAE的学习时我们引入了潜变量对样本进行编码,但是VAE缺乏一个tractable的likelihood,因此我们使用了变分推断来近似,那有没有什么方式能让我们使用潜空间来表示样本,并且有tractable的likelihood呢?这就是Normalizing Flow Model的用武之地。
Key
Flow Model的本质是使用一个可逆的、光滑的变换,将简单分布转换为复杂分布。
回顾一下VAE的思路,我们用一个神经网络来训练
但是需要enumerate所有可能的z❗️
而Flow Model的思路就是利用可逆变换来确定到底哪些z是与我们的x相关的,并且这样还能确定唯一的对应关系:
但是这样我们就需要保证z和x有相同的维度并且连续(在VAE中通过encoder压缩了z的维度,现在不行了)
Build¶
Recap on Probability
先让我们 预习 回忆一些概率论的知识:
首先是分布函数和密度函数在以后会用CDF(cumulative distribution function)和PDF(probability density function)来表示。
哦对,对于联合分布随机向量\(X\),如果他是高斯分布,他的密度函数可以表示为:
对于一个可逆变化\(f\),作用到随机变量\(Z\)后,\(X=f(Z)\)密度函数会变成:
对于一个可逆矩阵\(A\),有\(det(A^{-1})=det(A)^{-1}\)(因为\(det(M) det(M^{-1}) = det(I) = 1\))
就有:
也就是求算反函数雅各比矩阵的行列式转变为了求算正函数雅各比矩阵的行列式的倒数。
Idea
在对一个连续分布进行可逆变换时,如果这是一个线性变换,那么这个过程可以理解为对度量单位进行变换(米->英尺),但是显然对单位进行变换并不会让数据变得简单,但是如果我们做的是非线性变换,那么将是从不同角度审视数据(改变坐标系),让建模变得简单,并且由于是可逆的,所以不会丢失信息。
现在我们来正式的定义一个Flow Model:
Flow Model
- In a normalizing flow model, the mapping between \(Z\) and \(X\), given by \(f_{\theta}\): \(\mathbb{R}^n \rightarrow \mathbb{R}^n\) is deterministic and invertible such that:
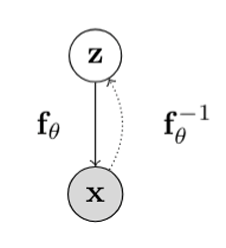
- by using change of variables, the marginal likelihood \(p(x)\) is:
- \(x,z\)连续且维数相同
我们的方法是施加一些列的可逆变换,将简单分布转化为复杂的:
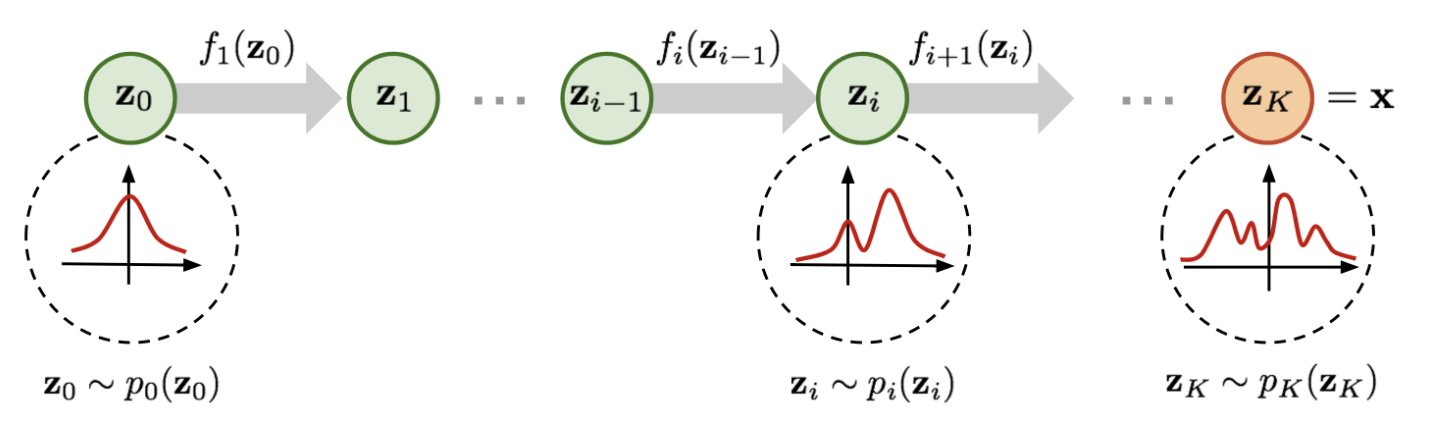
可以这样表示
- 从一个简单分布\(z_0\)开始,应用一系列的可逆变换,我没有省略\(\theta\)的脚注,因为每一个函数的训练参数都是不同的
接下来看一下最后的\(p_X(x)\)怎么推导:
推导
对Flow过程的第\(i\)个函数,有:
对等号两边取对数:
最后对整个过程累加:
这样一个path就是一个flow,如果我们将\(f\)替换为连续的分布\(\pi_i\),那么我们得到的就是一个normalized flow
需要注意的是:
- \(f_i\)的选择是easily invertable的(因为我们要对其进行训练,所以无论我们怎么改变\(\theta_i\),都要保证\(f_i\)是可逆的)
- 雅各比矩阵的行列式要易于计算
最终的criterion就是对数据集\(\mathcal{D}\)的negative log-likelihood
然后在这之中优化你的参数\(\theta_i\)
在得到一个训练好的模型后,直接sample:
Optimize¶
现在我们有了一个训练模型的整体思路,但是可以看到计算雅各比矩阵的过程是求n阶矩阵的行列式,这个过程的复杂度是\(O(n^3)\),所以需要一些方法来简化这个过程
一个思路就是使得雅各比矩阵是一个三角矩阵,这样我们就可以直接使用对角线上的元素来计算行列式,复杂度就变成了\(O(n)\)
原始的:
假如我们想要让J变为下三角矩阵,那么对角线右上的部分全为0,这就要求每一个\(x_i=f_i(\mathbf{z})\)只与\(z_i\)及\(z_i\)之前的变量有关(这一点有些类似于AutoRegressive Model)
Case Study¶
NICE¶
Non-linear Independent Component Estimation
NICE是Flow Model比较早的落地,基本思想是采用可逆的仿射变换 是这么个东西吧 来构造一个det = 1的雅各比矩阵
使用的Flow层被称为Additive Coupling Layer(加性耦合层):
也就是将z切割为两部分,第一部分保持不变,第二部分仅仅是平移一下,平移的参数\(m_{\theta}\)是一个可学习的神经网络
这个过程显然是可逆的,只需要移项就能做到,同时移项后\(m_{\theta}\)的项是常数项,求导后雅各比矩阵对角线上元素为1
同时在应用这些addictive coupling层后,还需要最后有一个rescaling layer:
这个层的雅各比矩阵对角线上元素为\(s_i\),所以雅各比矩阵的行列式为\(\prod_{i=1}^n s_i\)
Real-NVP¶
Real-valued non-volume preserving
不同于NICE的 volume preserving,Real-NVP采用了shifting+scale(仍旧是仿射变换affine transformation)的方式:
其中的\(s_{\theta}\)和\(t_{\theta}\)分别是缩放因子和平移因子,是d维输入n-d维输出的函数,\(\odot\)是element-wise product(逐元素乘法)
- 在缩放因子前使用了一个exp,这样就能保证缩放因子为正数
最后得到的雅各比矩阵行列式为:
code
import torch
import torch.nn as nn
class AffineCouplingLayer(nn.Module):
def __init__(self, input_dim, hidden_dim):
super().__init__()
# 定义生成s和t的神经网络
self.scale_shift_net = nn.Sequential(
nn.Linear(input_dim // 2, hidden_dim), # 输入x1的维度为input_dim//2
nn.ReLU(),
nn.Linear(hidden_dim, input_dim) # 输出s和t的拼接,各占一半维度
def forward(self, x, reverse=False):
x1, x2 = x.chunk(2, dim=-1) # 将输入分为x1和x2
st = self.scale_shift_net(x1)
s, t = st.chunk(2, dim=-1) # 拆分出s和t
s = torch.exp(s) # 对s取指数,确保缩放因子正定
if not reverse:
# 正向变换:h2 = x2 * s + t
h2 = x2 * s + t
h = torch.cat([x1, h2], dim=-1)
log_det = torch.sum(torch.log(s), dim=-1) # 对数行列式
return h, log_det
else:
# 逆向变换:x2 = (h2 - t) / s
x2 = (x2 - t) / s
x = torch.cat([x1, x2], dim=-1)
log_det = -torch.sum(torch.log(s), dim=-1)
return x, log_det
Autoregressive Flow¶
MAF¶
首先我们先来从AutoRegressive Model开始:
给定一个自回归模型的密度函数定义:
从先前的自回归视角,我们很清楚的知道这个过程的每个密度函数依赖于前\(i-1\)个变量
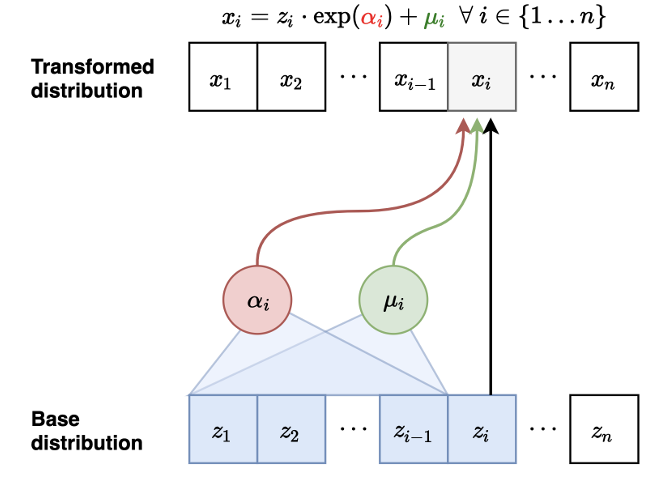
首先确定一个初始的\(z_1\),我们假设服从标准高斯分布,\(p(x)\)服从正态分布\(\mathcal{N}(\mu(x), \exp(\alpha(x)^2))\)
以此类推我们可以得到完整的正向推理过程
- Flow interpre:这个过程中的流可以理解为由标准高斯分布\(\mathbf{z}\) 到 \(\mathbf{x}\) 的变换,其中的可逆变换是由参数化的\(\mu_{i},\alpha_{i}\)决定的
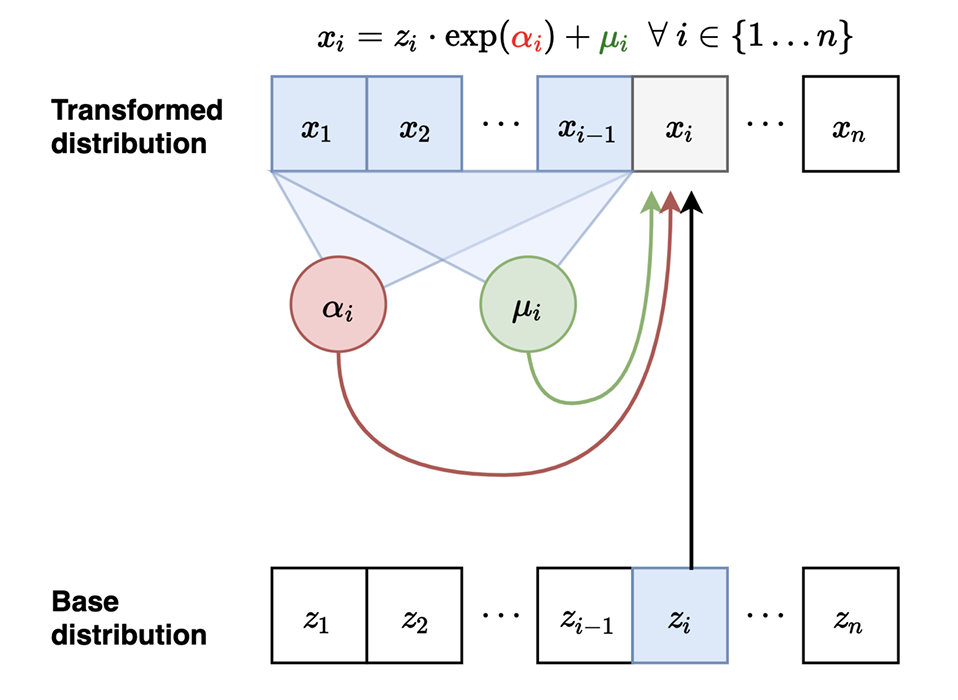
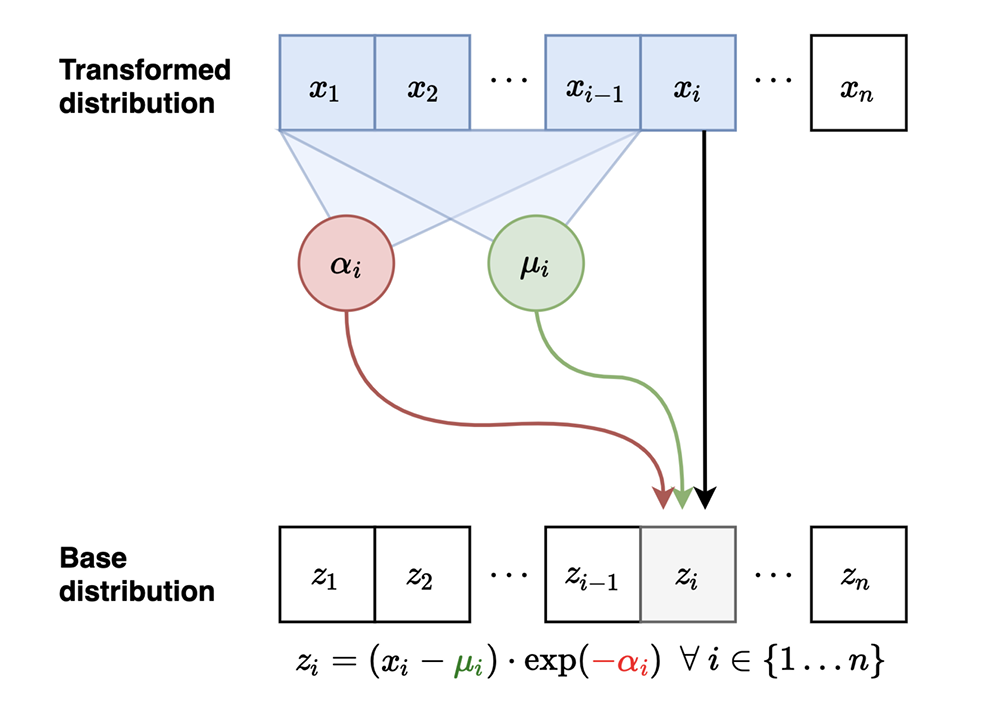
- forward过程中,每个x是按照顺序进行生成的
- 因为我们在forward过程中已经求算出各个x,因此在backward过程中,可以并行化计算(使用MADE等)参数表
IAF¶
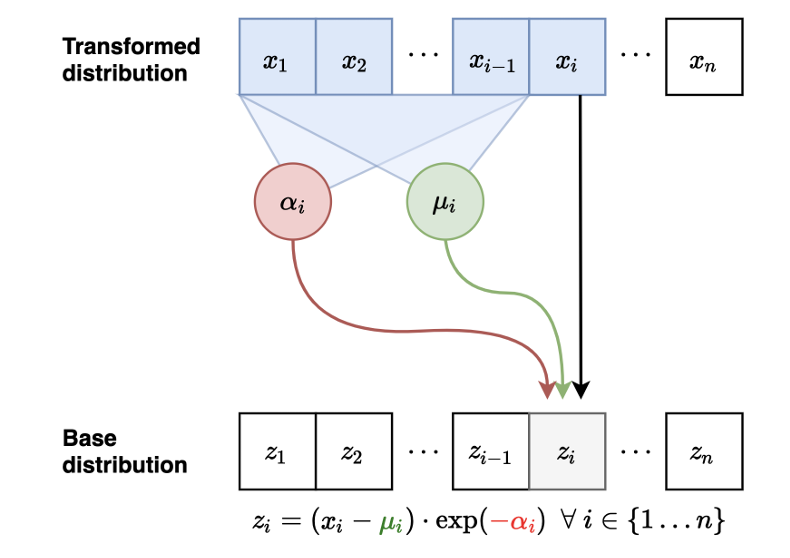
可以看到MAF的训练过程是可以并行化的,但是推理过程是顺序的,Inverse Autoregressive Flow 通过颠倒顺序,将推理过程进行并行化:
- 想要快速训练:MAF
- 想要即时生成:IAF
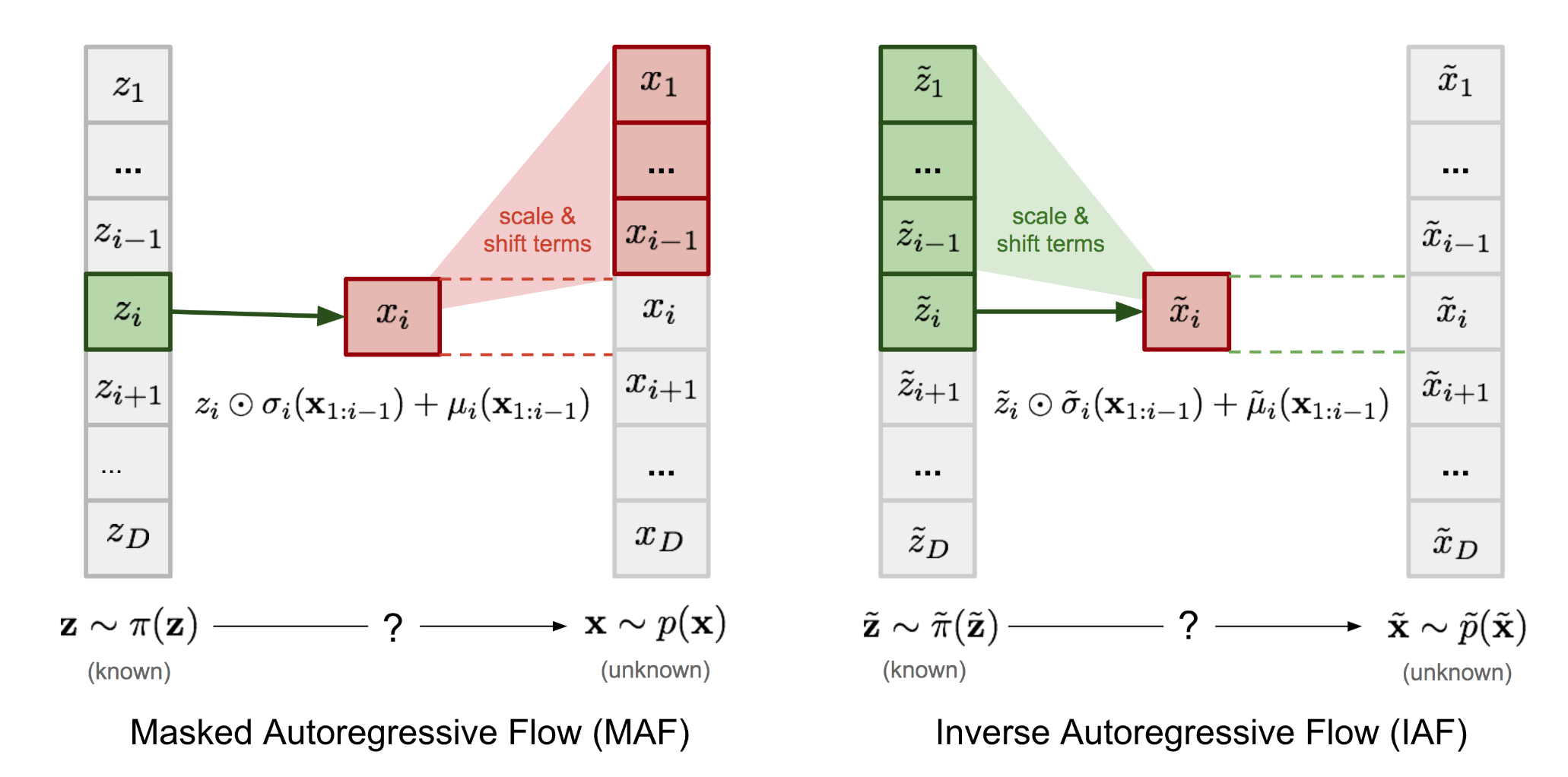
有没有结合了两者优点的模型?
Parallel Wavenet¶
如果我们能用MAF训练一个teacher model,再使用一个IAF作为student model,这样我们只需要保证学生老师之间的相似性(KL Div),避免了MAF采样的困难和IAF训练的问题,这就是Parallel Wavenet的思路
code
- Training
- Step 1: train MAF(teacher) via MLE
- Step 2: train IAF(student) to minimize KL div with teacher
- Test-time: Using student singly
References¶
留言