跳转至

Flow Matching

Abstract

在这一节中，我们来看一个与Diffusion Models非常相似的模型，Flow Matching。

我在这一节的内容参考的是MIT 6.S184。这个课程主要采用微分方程的视角来讲解Flow Matching和Diffusion，这个思想在Stefano的课上只是浅浅的提及，这里会详细展开。

Intro

Intro to ODE

我们先来从数学的角度看看ODE-based的Flow Matching。

从Flow的名字出发，想象一条河流，以及一片漂浮在河流上的叶子🍃

  • Vector Field: \(\mathbf{u}_t(x)\)

    这是最本质的概念，我们可以理解为描述河水流动的速度场，这也是我们在生成模型中需要学习的

    Definition

    \[ \mathbf{u}: \mathbb{R}^d \times [0,1] \to \mathbb{R}^d \quad (\mathbf{x}, t) \mapsto \mathbf{u}_t(\mathbf{x}) \]

    接受两个输入：空间位置\(\mathbf{x}\)和时间\(t\)，输出一个d维速度向量\(\mathbf{u}_t(\mathbf{x})\)，告诉我们在t时刻，\(\mathbf{x}\)这个点的河水流速和方向

    注意到我们这里的速度有角标\(t\)，这是因为速度场是随时间变化的，被称为非稳恒的（non-autonomous）

  • Trajectory: \(\mathbf{X}_t\)

    可以理解为一片叶子在河流中随时间变化的实际路径

    Definition

    \[ \mathbf{X}_t: [0,1] \to \mathbb{R}^d \quad t \mapsto \mathbf{X}_t \]

    接受一个时间\(t\)，输出一个d维位置\(\mathbf{X}_t\)，告诉我们在t时刻，这片叶子在什么位置，还需要满足约束：在任何时刻\(t\)，叶子在位置\(\mathbf{X}_t\)的流速为\(\mathbf{u}_t(\mathbf{X}_t)\)

  • ODE:

    这就是上述约束的数学表达，也就是我们说的ODE（Ordinary Differential Equation）

    Definition

    \[ \frac{d\mathbf{X}_t}{dt} = \mathbf{u}_t(\mathbf{X}_t) \tag{ODE} \]
    \[ \mathbf{X}_0 = \mathbf{x}_0 \tag{Initial Condition} \]

  • Flow: \(\psi_t(\mathbf{x}_0)\)

    flow就是ODE的解，任何一个初始位置给定为\(\mathbf{x}_0\)的叶子，在时间\(t\)时，都会到达\(\psi_t(\mathbf{x}_0)\)这个位置

    Definition

    \[ \psi_t: \mathbb{R}^d \to \mathbb{R}^d \quad \mathbf{x}_0 \mapsto \psi_t(\mathbf{x}_0) \]
    \[ \frac{d}{dt}\psi_t(\mathbf{x}_0) = \mathbf{u}_t(\psi_t(\mathbf{x}_0)) \tag{flow ODE} \]
    \[ \psi_0(\mathbf{x}_0) = \mathbf{x}_0 \tag{flow initial condition} \]

    对于一个给定初始条件的叶子，他的trajectory of ODE是被：

    \[ \mathbf{X}_t = \psi_t(\mathbf{x}_0) \]

    覆盖的，这个flow将所有可能的初始点以及他们各自随着时间变化的路径都封装在一个函数中

Summary

Vector fields, ODEs, and flows are, intuitively, three different descriptions of the same object:

vector fields define ODEs whose solutions are flows

Linear Autonomous Vector Field

Intro to Flow Matching

上面的例子中我们假设有一个这样的向量场，那是十分方便计算的，但现实中ODE很难找到一个解析解，因为计算ODE的解：

\[ \psi_t(\mathbf{x}_0) = \mathbf{x}_0 + \int_0^t \mathbf{u}_s(\psi_s(\mathbf{x}_0)) ds \]

其中的被积函数\(\mathbf{u}^\theta\)是神经网络，其中还嵌套着解自身，是递归结构的。

我们只能用数值方法来求解。

Euler's Method

最原始的方法求解ODE，就是Euler's Method。

欧拉法的本质源于导数的定义，在时间\(t\)时，我们处在\(\mathbf{x}_t\)这个位置，在计算得到当前瞬时速度后，我们假设在接下来h时间内，速度恒定不变，我们沿着这个方向走一小段。本质是用直线段近似真实轨迹

\[ \mathbf{X}_{t+h} = \mathbf{X}_t + h \mathbf{u}_t(\mathbf{X}_t) \quad \text{ t = 0, h, 2h, ..., 1-h} \]

欧拉法的局限性也很明显，因为速度是瞬时的，所以用直线段近似真实轨迹，每一步都会产生离散化误差，为了减小这个误差，我们需要将h设定为非常小的一个值，但这也导致了计算次数的大幅增加（n = 1/h）。这是一个一阶方法，其单步误差为\(O(h^2)\)，总误差为\(O(h)\)。

Runge-Kutta Method

为了减小误差，我们可以使用Runge-Kutta Method，这里我们介绍一个二阶方法：Huen's Method

\[ \mathbf{X'}_{t+h} = \mathbf{X}_t + h \mathbf{u}_t(\mathbf{X}_t) \tag{initial guess} \]
\[ \mathbf{X}_{t+h} = \mathbf{X}_t + \frac{h}{2} \left( \mathbf{u}_t(\mathbf{X}_t) + \mathbf{u}_{t+h}(\mathbf{X'}_{t+h}) \right) \tag{final guess} \]

休恩法意识到速度是会变化的，所以采用了h时间段的平均速度来近似真实轨迹。这对应着定积分中的梯形法则，而梯形法则显然比欧拉法的矩形法则来的更精确

在引入了数值求解方法后，我们有就将一个理想中连续的河流用离散化计算来simulation的方法了，现在我们引入flow model

Flow Modeling

我们的核心思想是将一个简单的distribution经过ODE的约束得到一个复杂的distribution

\[ \mathbf{X_0} \sim p_{init} \quad \text{random init} \]
\[ \frac{d}{dt}\mathbf{X}_t = \mathbf{u}^\theta_t(\mathbf{X}_t) \quad \text{ODE} \]

其中\(\mathbf{u}^\theta_t: \mathbb{R}^d \times [0,1] \to \mathbb{R}^d\)是神经网络，我们的目标是：

\[ \mathbf{X}_1 \sim p_{data} \equiv \psi_1^\theta(\mathbf{X}_0) \sim p_{data} \]

这样我们就得到了sample部分的算法：

Construct Training Targets

想要理解这部分的内容，首先有六个terms需要理解：

这里的：

  • Conditional \(\rightarrow\) "Per single data point"
  • Marginal \(\rightarrow\) "Across all data points"

我们对其中的内容上下对应进行解释：

Probability Path

概率路径的核心任务就是构建一座连续的、随时间 t 从0到1演化的“时空桥梁”，让处于世界A的任何一个噪声点，都能平滑地“流动”或“演化”到世界B，成为一个真实的、有意义的数据点。

\(p_t\)就代表了在时间\(t\)时，这座桥梁上所有点的概率分布状态。

先从一个简单的图片出发看一下两种概率路径的差异：

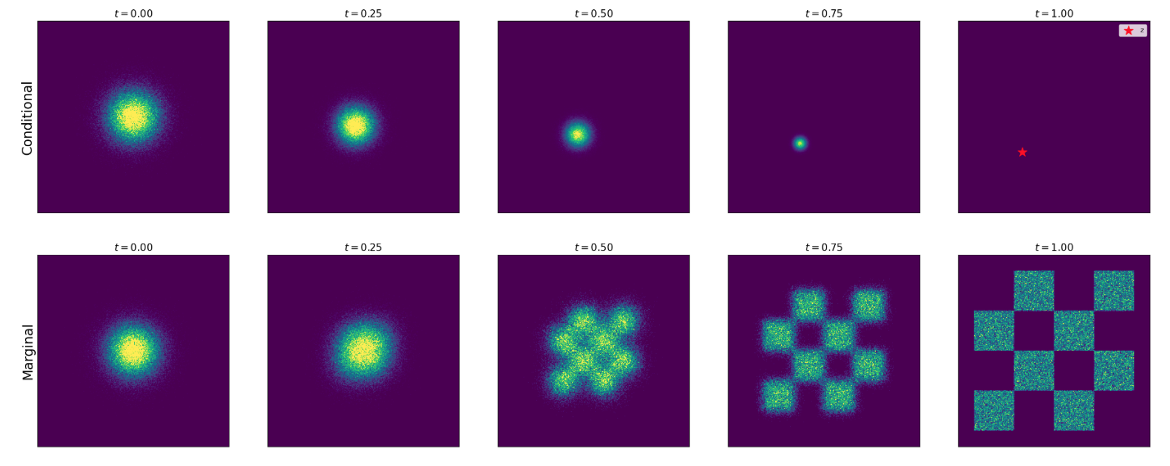可以看到条件路径的结果是一个单点，而边际路径是所有条件路径的结果的累加

我们给出定义：

Definition

条件概率路径描述一个点对点的演化过程。他定义一个概率分布，这个分布在时间\(t\)时的状态完全取决于给定的终点数据点\(z\)。

所以 Conditional(Interpolating) Path is a set of distribution \(p_t(x|z)\) over \(\mathbb{R}^d\) such that:

\[ p_0(\cdot | z) = p_{init}, \quad p_1(\cdot | z) = \delta_z \quad \forall z \in \mathbb{R}^d \]

其中\(p_{init}\)是初始分布，\(\delta_z\)是狄拉克分布，表示一个点\(z\)。

所有的条件概率路径可以induce一个边际概率路径：

边际概率路径首先先通过从\(p_{data}\)采样一个数据点\(z\)，然后通过条件概率路径得到一个分布\(p_t(x|z)\)，再积分得到

\[ z \sim p_{data} \quad \tag{1} \]
\[ x \sim p_t(\cdot|z) \Rightarrow x \sim p_t \tag{2} \]
\[ p_t(x) = \int p_t(x|z) p_{data}(z) dz \tag{3} \]

注意到我们这里并不能够得到这个积分的答案，但是可以发现当\(t\)分别取0和1时，边际概率路径就是\(p_{init}\)和\(p_{data}\)。

Gaussian Path

这里给出一个例子，我们选取正态分布作为两种路径的建模方式，同时设计一个时间参数\(t\)，来看一下随着时间变化两种路径的运行规律

\[ p_t(x|z) = \mathcal{N}(x; \mu_t(z), \sigma_t^2I) \]
\[ \mu_t(z) = t \cdot z \quad \sigma_t^2 = (1-t)^2 \]
  • 当\(t=0\)时，\(p_0(x|z) = \mathcal{N}(x; 0, I)\)，这意味着所有演化路径的起点都是标准正态分布
  • 当\(t=1\)时，\(p_1(x|z) = \mathcal{N}(x; z, 0)\)，这意味着所有演化路径的终点都是\(z\)

在路径中，分布的中心（均值）向\(z\)移动，同时方差逐渐减小，模糊性降低，最终到0。

Summary

为什么我们需要找到条件路径？

因为直接对边际路径进行建模是intractable的，但是条件路径是tractable的

我们的核心思想就是通过定义简单的可计算的条件路径间接定义出复杂的边际路径

Vector Fields

在先前的部分中，我们知道了两种路径，但是在ODE中，任何路径都需要一个向量场来驱动，现在我们来看这个向量场如何得到

先给出结论，我们使用Marginalization trick将条件向量场转换为边际向量场：

Marginalization trick

For every data point \(z \in \mathbb{R}^d\), let \(u_t^{target}(\cdot | z)\) be a conditional vector field, defined so that the corresponding ODE yields the conditional path \(p_t(\cdot | z)\), viz.,

\[ X_0 \sim p_{init}, \quad \frac{d}{dt}X_t = u_t^{target}(X_t | z) \quad \Rightarrow \quad X_t \sim p_t(\cdot | z) \]

Then marginal vector field:

\[ u_t^{target}(x) = \int u_t^{target}(x | z) \frac{p_t(x|z)p_{data}(z)}{p_t(x)} dz \]

follows the marginal path, i.e.,

\[ X_0 \sim p_{init}, \quad \frac{d}{dt}X_t = u_t^{target}(X_t) \quad \Rightarrow \quad X_t \sim p_t \]

同时我们可以发现积分号后方的分式其实是贝叶斯公式的展开，我们写回他其实就是后验概率\(p_t(z|x)\)（告诉我们，在时刻t，一个粒子的位置是x，那么他最终在位置z的概率是多少）

所以这个积分号其实是在求解一个后验概率的期望。这时我们就能将这个trick美化一下：

\[ u_t^{target}(x) = \mathbb{E}_{z \sim p_t(z|x)} \left[ u_t^{target}(x | z) \right] \]

这个公式告诉我们：

Summary

宏观的、边际的流速等于所有的微观的、条件的流速在后验概率下的期望（加权平均）。

条件向量场的作用就是对一个单点进行导航，这点显而易见，但为什么我们要提出这他？还是一样的道理，便于计算得到，以相同的Gaussian Path为例进行一次计算：

Conditional Vector Field under Gaussian Path

在时刻t，服从高斯路径\(p_t(x|z) = \mathcal{N}(x; \alpha_t(z), \beta_t^2(z)I)\)的点x，可以通过重参数化写为：

\[ x = \alpha_t z + \beta_t \epsilon \quad \epsilon \sim \mathcal{N}(0, I) \]

也可以通过flow model的视角来进行定义，也就是教材的思路：

\[ \psi_t(x_0) = \alpha_t z + \beta_t x_0 \]

这时\(\psi_t^{target}(\cdot|z)\)的ODE trajectory为：

\[ X_t=\psi_t^\mathrm{target}(X_0|z)=\alpha_tz+\beta_tX_0\sim\mathcal{N}(\alpha_tz,\beta^2I_d)=p_t(\cdot|z) \]
  • 这个conditional trajectory就是一个conditional probability path（满足marginalization trick定义）

其中\(\alpha_t\)和\(\beta_t\)是我们预设的关于时间的函数（比如\(\alpha_t = t, \beta_t = 1-t\)）。所以对于固定的初始噪声\(\epsilon\)和目标位置\(z\)，轨迹是确定的。同时记时间变换函数的导数为：\(\dot \alpha_t\)和\(\dot \beta_t\)

对任意\(z\),\(x \in \mathbb{R}^d\)，根据flow model的定义，我们对两边求t的导数：

\[ \begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\psi_t^{\mathrm{target}}(x_0|z)&=u_t^{\mathrm{target}}(\psi_t^{\mathrm{target}}(x_0|z)|z) \\ \dot{\alpha}_tz+\dot{\beta}_tx_0&=u_t^{\mathrm{target}}(\alpha_tz+\beta_tx_0|z) \\ \dot{\alpha}_tz+\dot{\beta}_t\left(\frac{x-\alpha_tz}{\beta_t}\right)&=u_t^\mathrm{target}(x|z) \quad \text{(reparameterization)} \\ \end{aligned} \]

这里的reparameterization技巧的解释：讲义在定义flow model的时候等式中的x都是哑变量，而实际上所有流模型的定义都是依赖\(x_0\)的，所以实际上第二行公式中的x就是一个给定的值\(x_0\)，而不是一个变量。我们知道任意位置：\(x = \alpha_t z + \beta_t x_0\)，用这个等式来反解出任意位置x再带回即可

整理得到：

\[u_t^\mathrm{target}(x|z)=\left(\dot{\alpha}_t-\frac{\dot{\beta}_t}{\beta_t}\alpha_t\right)z+\frac{\dot{\beta}_t}{\beta_t}x\]

Continuity Equation

同时讲义中也给出了一个连续性方程视角，用于解释Marginalization Trick的合理性

Continuity Equation

考虑一个flow model具有一个vector field \(u_t^{target}\)，其对应的ODE trajectory有条件：\(X_0 = p_{init}\)，那么他的轨迹\(X_t\)满足概率路径\(p_t\)，当且仅当：

\[ \partial_t p_t(x) = - div (p_t u_t^{target})(x) \quad \text{for all } x \in \mathbb{R}^d, t \in [0,1] \]

div是散度，在这里就是向量场在各个方向对自变量偏导的和

\[div(v_t)(x) = \sum^d_{i=1} \frac{\partial}{\partial x_i}v_t(x)\]

讲义中给出了一个直观易于理解的讲解：

对于等式左边，概率路径\(p_t\)的时间偏导描述的是随着时间变化，概率质量的合流入质量；对于一个流模型，一个粒子的轨迹\(X_t\)，遵循向量场\(u_t^{target}\)，在物理中，向量场的散度描述的是一个点在向量场中的流出量，然后我们再乘一个当前的质量，就得到了流出量，而由于概率质量是保守的，流入量等于负流出量，合理。

现在给出利用这个连续性方程证明marginalization trick：

Proof

Training

对于flow matching的损失函数，比较naive的想法就是衡量边际向量场和训练网络之间的MSE，同时采用先前提到的采样z的方法进行计算：

\[\begin{aligned}\mathcal{L}_{\mathrm{FM}}(\theta)&=\mathbb{E}_{t\sim\mathrm{Unif},x\sim p_t}[\|u_t^\theta(x)-u_t^{\mathrm{target}}(x)\|^2]\\&=\mathbb{E}_{t\sim\mathrm{Unif},z\sim p_\mathrm{data},x\sim p_t(\cdot|z)}[\|u_t^\theta(x)-u_t^\mathrm{target}(x)\|^2]\end{aligned}\]

但问题是即使采用采样z，我们仍然很难计算出目标向量场

为此我们想到，既然边际向量场不好计算，有没有可能直接用条件向量场，这里给出另一个损失定义：

\[\mathcal{L}_{\mathrm{CFM}}(\theta)=\mathbb{E}_{t\sim\mathrm{Unif},z\sim p_\mathrm{data},x\sim p_t(\cdot|z)}[\|u_t^\theta(x)-u_t^\mathrm{target}(x|z)\|^2].\]

直觉上来说，对边际向量场的处理变为条件向量场，我们是不能得到完整待计算的向量场的，但是下面的定理证明，对条件向量场的回归可以隐式地得到边际向量场：

Theorem

\[ \mathcal{L}_{\mathrm{FM}}(\theta) = \mathcal{L}_{\mathrm{CFM}}(\theta) + C \]

where \(C\) is independent of \(\theta\). Which means:

\[ \nabla_\theta \mathcal{L}_{\mathrm{FM}}(\theta) = \nabla_\theta \mathcal{L}_{\mathrm{CFM}}(\theta) \]
Proof

还是以之前的Gaussian Path为例：

Example

这时的loss就是：

\[ \mathcal{L}_{\mathrm{CFM}}(\theta)=\mathbb{E}_{t\sim\mathrm{Unif},z\sim p_\mathrm{data},x\sim\mathcal{N}(\alpha_tz,\beta_t^2I_d)}[\|u_t^\theta(x)-\left(\dot{\alpha}_t-\frac{\dot{\beta}_t}{\beta_t}\alpha_t\right)z-\frac{\dot{\beta}_t}{\beta_t}x\|^2] \]

讲义中定义的粒子轨迹是：

\[ x_t=\alpha_tz+\beta_t\epsilon\sim\mathcal{N}(\alpha_tz,\beta_t^2I_d)=p_t(\cdot|z) \]

将其代入上式

\[\mathcal{L}_{CFM}(\theta) = \mathbb{E}_{t\sim\mathrm{Unif},z\sim p_{\mathrm{data}},\epsilon\sim\mathcal{N}(0,I_d)}[\|u_t^\theta(\alpha_tz+\beta_t\epsilon)-(\dot{\alpha}_tz+\dot{\beta}_t\epsilon)\|^2]\]

如果我们取\(\alpha_t = t, \beta_t = 1-t\)，此时的probability path被称为(Gaussian) CondOT probability path，此时的loss：

\[\mathcal{L}_{\mathrm{cfm}}(\theta)=\mathbb{E}_{t\sim\mathrm{Unif},z\sim p_{\mathrm{data}},\epsilon\sim\mathcal{N}(0,I_d)}[\|u_t^\theta(tz+(1-t)\epsilon)-(z-\epsilon)\|^2]\]

这也是Stable Diffusion3和Meta Movie Gen的fm损失函数

最终的Algo如下：

Conditional Flow Matching

其实这部分的diffusion讲的也很好，但是最近在写论文没时间看了，抽空补上哈（）

留言

欢迎在下方交流~