Energy-based Models¶
约 1748 个字 6 张图片 预计阅读时间 6 分钟
Intro¶
EBMs 具有以下特点:
- Flexible model arch
- Stable training
- Flexible composition
这点与之前的两类模型不同:
进行一个大体上的区分的话,先前学习的
-
VAE、Flow、AR都属于基于似然的模型,他们的特点是具有严格的概率解释和训练目标,但是模型结构相对固定,难以灵活调整。
-
GANs属于implicit models,他不具有概率解释,这样使得模型的架构更加灵活,但同时训练不太方便
EBMs也是基于似然的模型
Recap¶
回忆我们之前学习的概率模型,我们构建的pdf有以下两点要求:
- Non-negative
- Sum to 1
通常来说构建一个非负的pdf是容易的,用平方、指数、绝对值都可以的,但是归一化并不简单,需要计算积分
Common usage
-
\(g_{\mu, \sigma}(x) = e^{-\frac{(x-\mu)^2}{2\sigma^2}} \rightarrow \sqrt{2\pi\sigma^2}\)
-
\(g_{\lambda}(x) = e^{-\lambda x} \rightarrow \frac{1}{\lambda}\)
-
Exponential family: Normal, Poisson, beta, gamma, etc
- \(g_{\theta}(x) = h(x) \exp(\theta \cdot T(x)) \rightarrow \exp{A(\theta)}\) where \(A(\theta) = \log \int h(x) \exp(\theta \cdot T(x)) dx\)
在进行归一化操作后,我们组合这些函数进行建模,就有了:
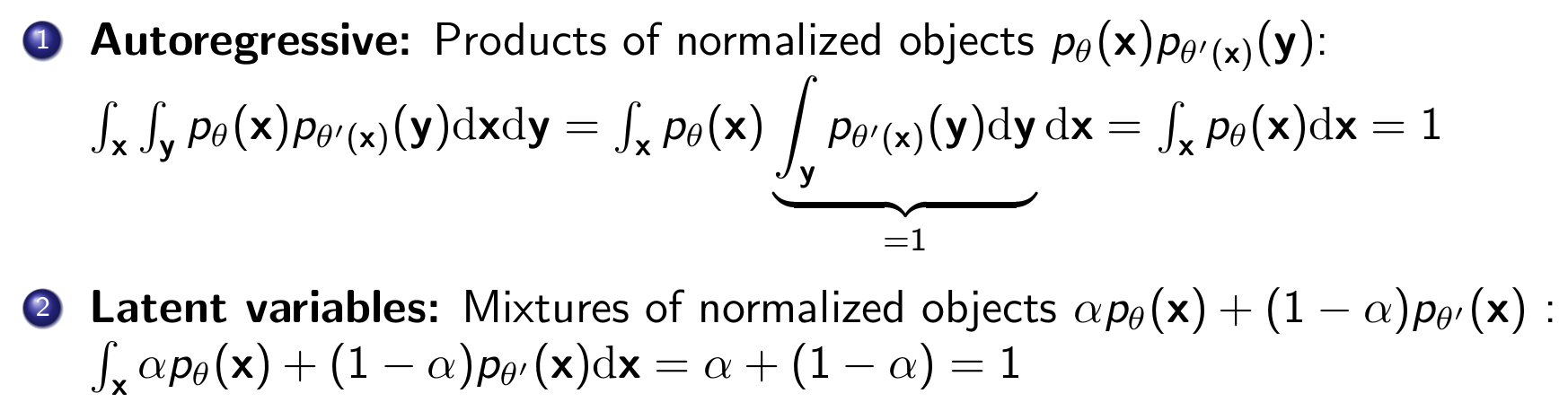
可以看到这些模型都是将normalization constant确定为1,而在EBMs中,我们不仅不会控制这个常数,甚至不会精确算出来它
Build¶
\(Z(\theta) = \int e^{f_\theta(x)} dx\) is called the Partition Function
可以看到我们使用了指数形式,有以下原因:
- 可以捕获巨大的概率变化,并且一般是使用log-probability
- 很多的概率分布都是指数族的
- 满足一些物理定律
- 实际上energy这个名字的来源就是物理学(最大熵、热二定律),在这里就是指\(-f_\theta(x)\)
Pros: extreme flexibility(any function \(f_\theta\) can be used)
Cons:
- Z如果难以计算,那么sampling就很难进行
- No feature learning
- Curse of dimensionality
Application¶
虽然进行单个样本的采样很难,但是对于两个样本点的比较会比较容易,因为做比值后,Z就约去了:
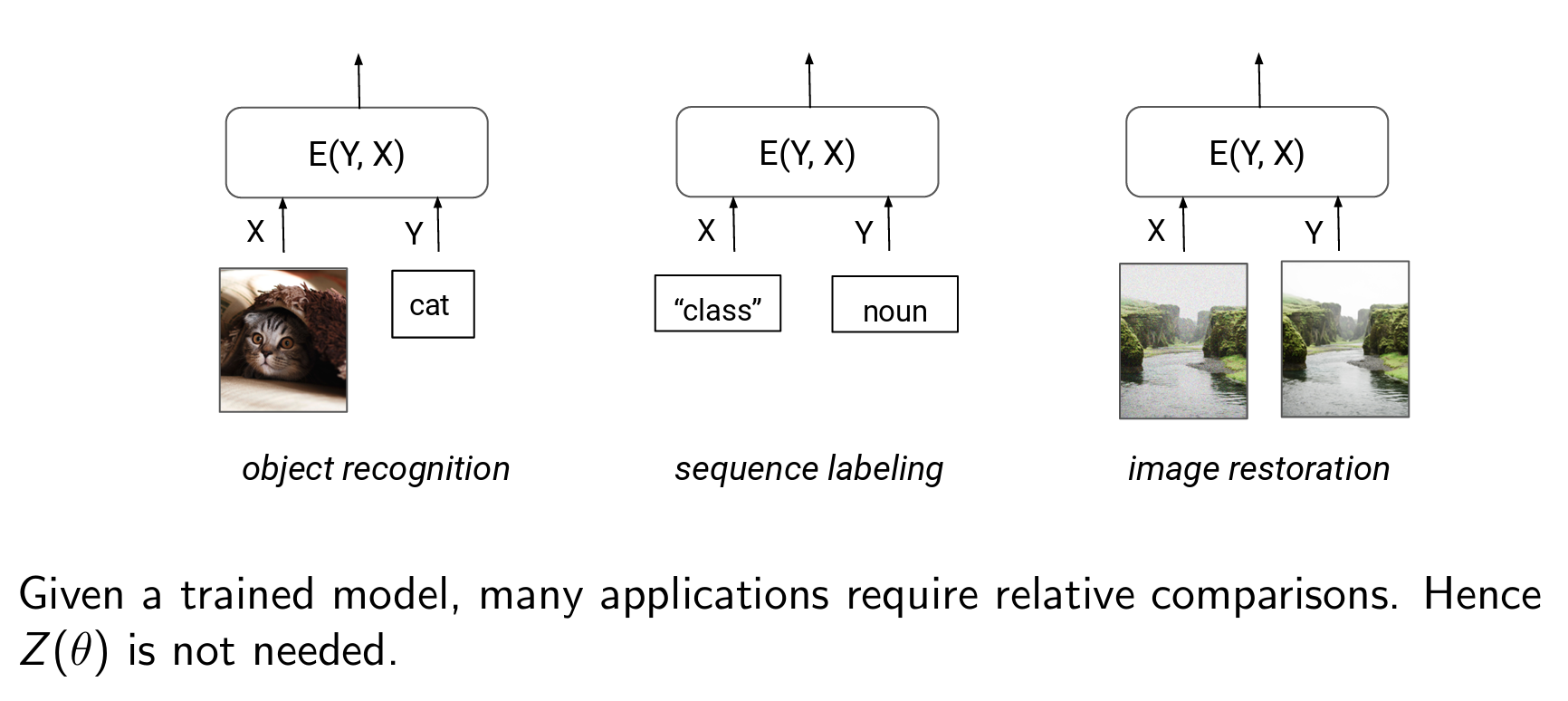
Training¶
在前面的内容中我们讨论了EBMs的定义,以及利用EBMs进行两个样本点比较,但这是建立在已经有一个训练好的EBM基础上,现在我们的问题是如何训练一个EBM,也就是maximize \(p_\theta(x)\)
一个直观的感受就是,对于这样的分数,如果我们能增大分子,减小分母,那么分数值就会增大,这就是 Contrastive Divergence
Prove
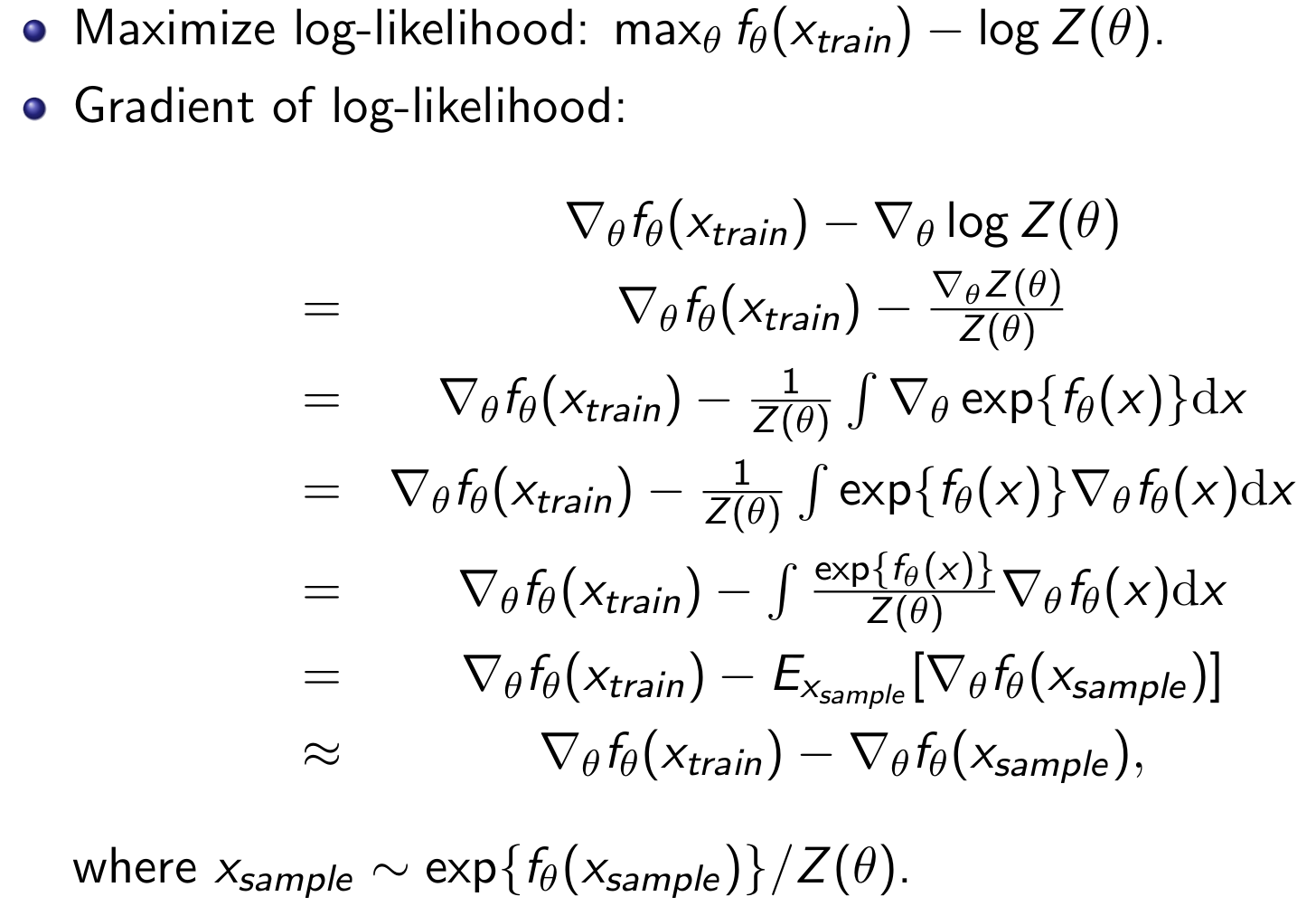
最后的那步近似就是sample的MC近似
Sampling¶
现在的问题来到我们应该如何sample:
因为我们没有办法计算\(Z\),所以还是采取比较的思想:
\begin{algorithm}
\caption{Markov Chain Monte Carlo(MCMC) for EBM}
\begin{algorithmic}
\REQUIRE initial parameters
\STATE Initialize $x^0$ randomly, set $t = 0$
\REPEAT
\STATE $x' \gets x^t + \text{noise}$ \COMMENT{Perturb current solution}
\IF{$f_\theta(x') > f_\theta(x^t)$}
\STATE $x^{t+1} \gets x'$ \COMMENT{Always accept better solutions}
\ELSE
\STATE $\text{Accept } x^{t+1} = x' \text{ with probability } \exp(f_\theta(x') - f_\theta(x^t))$
\ENDIF
\STATE $t \gets t + 1$
\UNTIL{t = T}
\end{algorithmic}
\end{algorithm}
这有点像模拟退火,为了避免停留在一个local,我们参考了一一个概率选择那个较差的sample
-
理论上来说\(x^T\)会收敛到\(p_\theta(x)\)(在\(T \rightarrow \infty\)时)
- 因为他满足一个叫detailed balance的条件:可以看到这个式子在x达到\(p_\theta(x)\)时,x'不会再进行更新
\[ p_\theta(x) \cdot T(x, x') = p_\theta(x') \cdot T(x', x) \]这里\(T(x', x)\)是指x到x'的transitioning概率
-
实际中,需要一个大量的循环才能达到收敛
也就是说,即使我们拥有一个很好的\(f_\theta\),我们也需要大量的精力去sample,并且我们看到,使用contrasive divergence进行的训练的时候本身就是一个sample的过程,所以即使是训练也是十分昂贵的
一个改进:
\begin{algorithm}
\caption{unadjusted Langevin MCMC}
\begin{algorithmic}
\REQUIRE initial parameters
\STATE Initialize $x^0 \sim \pi(x)$ randomly, set $t = 0$
\REPEAT
\STATE Add random noise $z \sim N(0, 1)$
\STATE $x^{t+1} \gets x^t + \epsilon \nabla_{x} \log p_\theta(x^t) + \sqrt{2 \epsilon} z^t$
\UNTIL{t = T}
\end{algorithmic}
\end{algorithm}
这个朗之万动力算法的思路和之前的差不多,就是沿着有噪声的对数似然梯度上升方向来生成
- 可以在T趋向∞和\(\epsilon \rightarrow 0\)时收敛到\(p_\theta(x)\)
- 对于连续的EBMs,\(\nabla_{x} \log p_\theta(x) = \nabla_{x} f_\theta(x)\)
这个方法的好处在于我们现在不是随机游走,而是在梯度方向上进行移动
Better Training¶
虽然我们得到了一些比较好的sample方式,但是在训练时如果还是使用内部循环的这种方式,依然是无法接受的,下面提出一些新的训练方法
Score Matching¶
回顾一下energy-based:
现在给出score function:
这里和之前朗之万那边一样,没有Z是因为对x求梯度后,Z就是0了,所以对于归一化常数,我们的score function有很好的效果:

这样我们就不用求partition function了,本质上我们没有进行改变,但是重新换了一种计算方式,因为基于梯度的方法也可以从另一个角度进行两个概率点的比较,而不是在partition function中比较占比大小
现在我们提出训练目标函数:
Score Matching:minimize the Fisher divergence between \(p_{data}\) and the EBM \(p_\theta \propto \exp{f_\theta(x)}\)
现在的问题是:我们没有\(p_{data}\)(有了还训练个🥚)
好消息是我们可以用分部积分把\(p_{data}\)给消掉:
Prove in 1 dimension


在这种一维情况的证明中,nabla算子就是求导,在进行积分时,\(p_{data}\)在正负无穷处为0,所以可以消去
最终我们得到的结果是:
此时我们想通过小样本batch训练的话,\({x_1, x_2, \dots, x_n} \sim p_{data}(x)\),用经验平均估计:
再采用stochastic gradient descent
- 这样我们就不用在EBM中进行sample了!
- 但是海赛矩阵很难算!!!()()()🥵
Noise contrastive estimation¶
TBD
留言