跳转至

Parallel Algorithms

约 2900 个字 46 行代码 预计阅读时间 10 分钟

Intro

intro

对于问题\(a+b\)，我们可以在怎样的时间复杂度内解决呢？

一是\(O(\log a + \log b)\)，他对应的是用图灵机来解决

二是\(O(1)\)，他对应的是用Random Access Machine来解决

我们今天来讨论的是\(O(1)\)的解决方案。

定义

今天我们讨论的并行算法是基于RAM的，使用parallel RAM（PRAM）模型。

  • 已知一段无限长的cell sequence，每个cell可以存储一个整数，同时每一块cell有自己独立的地址。
  • 有一定数量的CPU，每个CPU中有常数个寄存器，每个寄存器有自己的名字。
  • 每个CPU可以执行以下操作：
    • 寄存器赋值：常数或者其他寄存器的值
    • 运算：整数的加减乘除
    • 比较：两个寄存器的大小
    • 内存访问：寄存器内部存储一个内存的地址，通过另一个寄存器write/read对应地址的cell的值

由于多个CPU同时对内存进行读写，所以需要考虑内存的冲突问题，根据冲突的解决方式，PRAM模型可以分为以下几种：

  • CREW：Concurrent Read Exclusive Write，允许多个CPU同时读取同一个cell，但是写入时需要独占
  • EREW：Exclusive Read Exclusive Write，写和读都是独占的
  • CRCW：Concurrent Read Concurrent Write，允许多个CPU同时读取和写入同一个cell

Analysis of Parallel Algorithms

在并行算法的设计中，我们需要换一个视角进行分析，或者说进行一种新的学习。

以一个很简单的例子开始：Summation

  • input：\(A_1, A_2, \cdots, A_n\)
  • output：\(S = \sum_{i=1}^{n} A_i\)

很容易想到我们应该使用二分法进行求和：

想象这个求和过程是一棵二叉树，每个节点代表一个二分计算的子问题称为\(B(h,i)\)，其中\(h\)是树的高度，\(i\)是节点在第\(h\)层的编号。

那么这个过程的伪代码如下：

for i in range(n): pardo  #pardo 是并行计算的意思
    B(0,i) = A[i] # 初始化

for h in range(1, log 2 n):
    for i in range(1, n/2^i): # 每层有n/2^i个问题
        B(h,i) = B(h-1,2i-1) + B(h-1,2i) # 每个问题等于两个子问题之和

return B(log 2 n, 1) # 最后返回根节点的问题

定义

在并行算法中，我们定义时间复杂度需要依赖processor的个数

  • \(T_p(n)\)：\(p\)个processor解决问题规模为\(n\)的时间复杂度

    • Work：\(=T_1(n)\)是\(1\)个processor工作时的时间

      每一个原子操作的和的总时间

    • Depth：\(=T_{\infty}(n)\)是\(p=\infty\)时的时间复杂度

      最长的依赖链的长度，用来形容algorithm有多么的parallel（）好像在cy的ppt中这部分就是时间复杂度

现在我们想求的是当我们有任意的\(p\)个processor时，\(T_p(n)\)是多少。

很直观的结果是\(T_p(n) = \frac{W}{p}\)，但是这个结果是错误的，因为很明显我们每一级的计算是依赖于前一级的计算的，但是我们可以得到一个下界：

\[ T_p(n) \geq max(D, \frac{W}{p}) \]

对于一般算法所需要的上界，我们有Brent's Theorem：

\[ T_p(n) \leq \frac{W}{p} + D \]
证明

整个工作由于是分层进行的，有相互依赖的关系，我们不仿按照每一层的工作进行组的划分：

\(g_1, g_2, \cdots, g_D \text{ and } \sum_{i=1}^{D} g_i = W\)

在每层中我们所需要的时间就是可求的了：

\(T_p(n) = \sum_{i=1}^{D} \lceil \frac{g_i}{p} \rceil \leq \sum_{i=1}^{D} (\frac{g_i}{p} + 1) = \frac{W}{p} + D\)

这样我们在summation问题中，\(W = n\)，\(D = \log_2 n\)，可以直接得到结果

我们考虑一个问题：

对于两个问题\(A_1, A_2\)，他们分别有\(W_1, W_2\)个原子操作，\(D_1, D_2\)个依赖链

那么我们分别在串行和并行的情况下，求解他们的\(W\)和\(D\)

  • 串行：\(W = W_1 + W_2\)，\(D = D_1 + D_2\)
  • 并行：\(W = W_1 + W_2\)，\(D = max(D_1, D_2)\)

通过上面的结果，我们可以得到一个思路：

在并行算法中，我们尽可能要在保证相同\(W\)的情况下，尽可能减少\(D\)（换句话说，我们用并行算法提高的是\(D\)的优劣，但是\(W\)的优劣也要尽可能的保证）

接下来的例子是：

Prefix Sum

  • input：\(A_1, A_2, \cdots, A_n\)
  • output：\(\sum_{i=1} A_i, \sum_{i=1}^{2} A_i, \cdots, \sum_{i=1}^{n} A_i\)

也就是求出前缀和

在串行算法中：

\[ W = O(n) \quad D = O(n) \]

一个简单的并行算法是：我们对每一项求和进行二分并行计算，其中的每一项工作量是\(O(j)\)，所以

\[ W = \sum_{j=1}^{n} O(j) = O(n^2) \quad D = O(\log n) \]

可以看到虽然并行算法对\(D\)的优化很大，但是增大了\(W\)，所以这个算法并不是一个好的算法。

现在我们对这个算法进行优化：

定义

我们定义一个tag，\(C(h,i)\)，表示在第\(h\)层，第\(i\)个节点位置上的tag值

这个值是从最左边的叶子开始，一直到这个节点的叶子节点的和

像这样：

        o
       / \
      o   o  //C(1,1) = A1 + A2   C(1,2) = A1 + A2 + A3 + A4
     / \  / \
    o  o  o  o
    A1 A2 A3 A4

这是我们的目标就是计算：\(C(0, 1), C(0, 2), \cdots, C(0, n)\)

        o
       /  \
      o    o  
     / \   / \
    o  o  ｜o｜ o //计算C(1,3)
   / \ /\  /\  /\
  o o o o  o o  o o
[A1 .. A4][A5A6]

我们来计算\(C(h, i)\)（以\(h=1, i=3\)为例）

我们将这个节点的叶子分为；两个部分，1-4和5-6

1-4的和是该节点的父亲的左兄弟的C值，5-6是该节点的B值（B是当前节点的叶子值之和）

得到：

\[ C(h, i) = C(h-1, \frac{i-1}{2}) + B(h, i) \]

这是左儿子的计算方法，右儿子就相对简单，直接等于父亲的C值

\[ C(h, i) = C(h-1, \frac{i}{2}) \]

当节点是每一层的第一个节点时，\(C(h, 0) = B(h, 0)\)

现在对复杂度进行分析：

我们要对B值先进行计算，然后求出C值，再对这两个值进行求和

\[ W_B = O(n) \quad D_B = O(\log n) \]
\[ W_C = O(n) \quad D_C = O(\log n) \]

将这两个值串行求和

\[ W = O(n) \quad D = O(\log n) \]

Example

并行排序

使用归并排序，我们也能将工作过程写为一个二叉树，在第\(i\)层中，我们已经将所有元素分成了\(2^i\)个部分，每个部分有\(\frac{n}{2^i}\)个元素，进行两两合并，这时每个节点的\(W\)是\(O(\frac{n}{2^i})\)，\(D\)也是\(O(\frac{n}{2^i})\)，在这一层中所有节点进行求和，所以\(W\)是\(O(n)\)，\(D\)并行处理的，因此还是\(O(\frac{n}{2^i})\)

最后对每一层进行求和，\(W\)是\(O(n \log n)\)，\(D\)是\(O(n)\)

在这里可以看出我们算法的瓶颈在于merge，如果我们能对merge进行优化，那么我们就能提高整个算法的效率。

因此问题变成了：

merge

给定两个有序的数组\(A\)和\(B\)，如何将他们合并为一个有序的数组\(C\)？

  • serial：得到每个元素在另外一个数组中的位置（rank），然后放进新的数组
for i in range(1, n): pardo
    C[i + rank(i, B) - 1] = A[i]
    C[i + rank(i, A) - 1] = B[i]

这个rank法得到的\(W\)是\(O(n)\)，\(D\)是\(O(1)\)

是一个不错的结果，但问题是我们怎样得到rank？

问题变成了：

rank

在两个有序数组中，如何找到一个元素在另外一个数组中的位置：

\(A\)的第\(i\)个元素在\(B\)中的rank是\(rank(i, B)\)

\(B\)的第\(j\)个元素在\(A\)中的rank是\(rank(j, A)\)

  • serial:

在两个数组中设置双指针：

i = 1
j = 1
while i <= n and j <= n:
    if A[i] < B[j]:
        rank(i, B) = j
        i += 1
    else:
        rank(j, A) = i
        j += 1

这个算法得到的\(W\)是\(O(n)\)，\(D\)是\(O(n)\)，不太好，是纯种串行（）

  • Binary Search：
for i in range(1, n): pardo
    rank(i, B) = binary_search(A, B[i])
    rank(i, A) = binary_search(B, A[i])

这个算法得到的\(W\)是\(O(n \log n)\)，因为每次二分查找的复杂度是\(O(\log n)\)，然后有\(n\)个元素

\(D\)是\(O(\log n)\)，因为每次二分查找可以并行执行，深度就是单次二分查找的深度

这两种算法一种是W好，一种是D好，那么我们能不能找到一个W和D都好的算法呢？

  • parallel ranking

这个算法是结合了上述两种方法的一种算法，在serial中，我们使用完全串行，导致深度很大，在binary中，我们每一步都进行二分查找，导致工作量很大，在这个方法中，我们只挑选一部分关键元素进行二分查找，然后对这些关键元素间隔出的数组块进行并行的串行连接，这样就能大大减小深度，同时也能减小工作量

parallel ranking

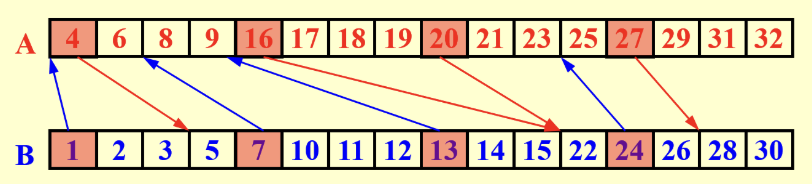
  1. 间隔\(k\)个元素，对两个数组挑选一个元素\(A[i], B[i]\)进行binary ranking，箭头指向对方数组中的位置，每对箭头将两个数组分成k个group

    注意：这里不会形成交叉（推理一下就能知道，大小关系会发生矛盾）

    rank-1

    \[ W = O(\frac{2n}{k} \log n) \quad D = O(\log n) \]

  2. 并行地将每个group进行serial rank

    \[ W = O(n) \quad D = O(k) \]

Total:

\[ W = O(\frac{2n}{k} \log n + n) \quad D = O(\log n + k) \]

当\(k = \log n\)时，\(W = O(n)\)，\(D = O(\log n)\)，是一个不错的结果

得到较好的ranking方法后，我们在计算merge开销时就能得到\(W = O(n)\)，\(D = O(\log n)\)

这时候整个mergesort的\(D_i\)可以对\(O(\frac{n}{2^i})\)取对数，求和后得到\(D = O((\log n)^2)\)

Maximum Finding

给出\(n\)个数，求出其中的最大值

  • serial:

    \(W = O(n) \quad D = O(n)\)

  • summation algorithm

    将加法改成max

    \[ W = O(n) \quad D = O(\log n) \]

  • compare all pairs

    在不考虑Work的情况下，我们使用并行：

    for i in range(1, n): pardo
    B[i] = 0 # 初始化 标记值全部为0
for every pair (i, j): pardo
    if A[i] < A[j]:
        B[i] = 1  #将小的标记为1
    else:
        B[j] = 1

这样最终标记值还是0的元素就是最大值

\[ W = O(n^2) \quad D = O(1) \]

问题

在这里我们会发现对标记值进行更改时可能多个processor同时进行，因此要允许，但是还要保证写入时的数据是相同的，我们在这里使用 common CRCW 模型

  • Divide and Conquer

    1. 将整个问题拆分成\(\sqrt{n}\)个子问题，每个部分有\(\sqrt{n}\)个元素
    2. 在每个子问题中用compare all pairs的方法求出最大值

    写出递推关系式：

    \[ W(n) = \sqrt{n} W(\sqrt{n}) + O(n) \]
    \[ D(n) = D(\sqrt{n}) + O(1) \]

    最后解得：

    \[ W(n) = O(n \log \log n) \quad D(n) = O(\log \log n) \]

同样的我们会想，有没有能够降低Work的方法：

  • 分块后再D&C

    1. 将整个问题拆分成\(k\)个部分，每个部分有\(\frac{n}{k}\)个元素
    2. 在每个子问题中用compare all pairs的方法求出最大值
    3. 将每个子问题的最大值进行D&C比较，得到全局最大值

第一步的\(W\)是\(O(\frac{n}{k})\)，\(D\)是\(O(\frac{n}{k})\)

第二步的\(W\)是\(O(k \log \log k)\)，\(D\)是\(O(\log \log k)\)

求和，令\(k = \log \log n\)，得到：

\[ W = O(n) \quad D = O(\log \log n) \]
  • Random Sampling

通过随机取样可以得到一个\(W=O(n) \quad D=O(1)\)的算法

思想就是通过随机取样后并行两两比较，不断缩小数组的规模，直到数组规模达到\(\sqrt{n}\)，然后使用compare all pairs的方法

  1. 在A中随机取样\(n^\frac{7}{8}\)个元素，形成数组\(B\)
  2. 在B中分块，每块有\(n^\frac{1}{8}\)个元素，这样\(B\)就有\(n^\frac{3}{4}\)个块
  3. 用compare all pairs的方法求出每一组的最大值
  4. 得到一个C只有\(n^\frac{3}{4}\)个元素的数组
  5. 对C分为\(n^\frac{1}{2}\)个块，然后对每个块进行compare all pairs，得到最大值
  6. 得到D，D中只有\(n^\frac{1}{2}\)个元素，然后对D进行compare all pairs，得到最大值

random sampling：

for i in range(1, n^(7/8)): pardo
    B[i] = random select(A)

这样得到的算法准确性很高，出现错误的概率是\(O(\frac{1}{n})\)

评论区

欢迎在下方留言~