Fundamentals of Data Structure

约 4036 个字 288 行代码 预计阅读时间 17 分钟

错题集：

1. For a sequentially stored linear list of length N, the time complexities for deleting the first element and inserting the last element are O(1) and O(N), respectively.

A：False

R：sequencial --> 顺序映射 一定是数组 不是链表

顺序映射就是地址按顺序连接，知道第一个就知道其他所有

链表则不知道，但好处是随时要到空间，但是占用内存过多时不能给出连续大片空间

2. If the most commonly used operations are to visit a random position and to insert and delete the last element in a linear list, then which of the following data structures is the most efficient?

A. doubly linked list

B. singly linked circular list

C. doubly linked circular list with a dummy head node（好处是可以前进后退）

D. sequential list

A：D

R：Random access-->一定是数组

链表中每个节点的地址都储存在前一个节点中，无法达成随机访问，只能有一步知道下一步的地址

3. To merge two singly linked ascending lists, both with N nodes, into one singly linked ascending list, the minimum possible number of comparisons is:

A：N

R：第一个元素比较a1次后插入，第二个比a2次……

直到a1+a2+…… = N后，其他的元素不用比较直接放在最后面即可 极端情况是每一个元素都比另外一个数组小，那么第一个元素比较N次后，其他元素全部插在后面，也同样是N次

4. It is always possible to represent a tree by a one-dimensional integer array.

A: T

5. If a general tree T is converted into a binary tree BT, then which of the following BT traversals gives the same sequence as that of the post-order traversal of T?

A: In order traversal. 找一个树的例子试一下

6. In a binary search tree, the keys on the same level from left to right must be in sorted (non-decreasing) order.

A: T

7. 判断BST decision tree 的合法性：对偶数来说一定左右平衡 奇数是自己选定走左边（或者右边），选定好了一定对每个子树来说都是左边大于右边（或者相反）不会前后矛盾

Lec 00

3 types of structures

sorting

hash

preparing for ads(queue stack)

further studying

测试数据的要求：

1. 分支测试：对每个if-else都要进入
2. 边界测试：数据范围的最值

​ 需要在最大数据时找到最快数据和最慢数据

Lec 01 Algorithm Analysis

Time & space complexity : machine and compiler independent

mostly about time

Assumption:

• instructions are excuted sequential
• simple instruct
• integer size is fixed and infinite memory

usually analyzing the average and worst cases time

O: worst case(take the smallest f(N) to illustrate )

Tx <= Cfx

Ω: best case(take the largest f(N) to illustrate )

Tx >= Cfx

ø: completely same

Tx = Ofx = Ωfx

o: infinitely related to O

operation:

T1 + T2 = maxone

T1*T2 = multiple

Lec 02

Q:求已知数列的最大子列

1. 暴力穷举 O(N^3)
2. 优化this sum求法 减少一组循环
3. Divide and conquer O(nlogn)
4. On-line Algorithm不走回头路

this = max = 0
for(...): 
​   if:this > max: max = this 
    else if: this < 0: this = 0

Q:binery search

use loop O(logn)

• usually used in static and ordered data

Lec 04 ADT

Data type = object + operation

Abstract:

representation is separated from implementation

each operation is isolated

Polynomial ADT

coefficient and exponent

typedef struct // array way
{
  int Coeffientarray[maxdegree + 1];
  int HighPower;
}*Polynomial;

(X) when poly is sparse but the operation is dense

typedef struct poly_node *poly_ptr;
struct poly_node
{
  int Coe;
  int Exp;
  poly_ptr next;
};
typedef *poly_ptr a;

Multilists

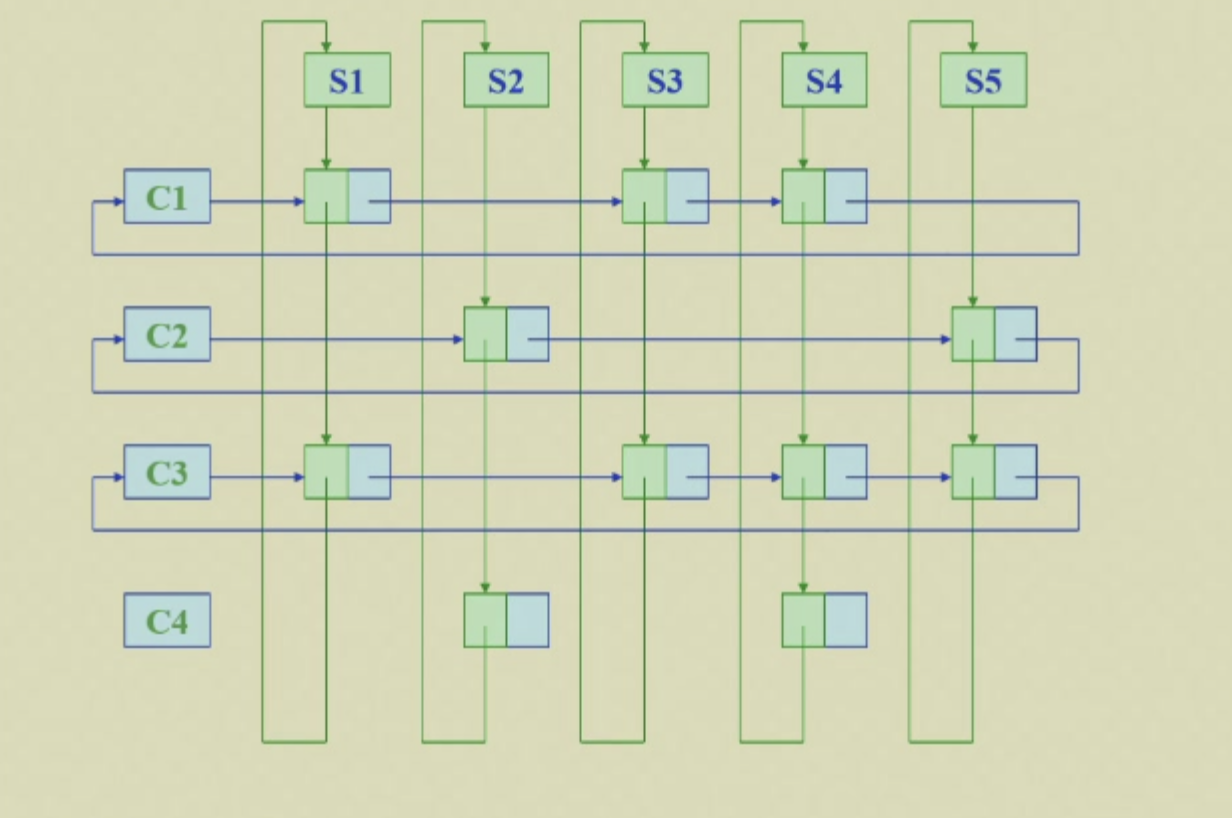
Lec 05 Linear List

Stack ADT

帮助系统临时存放或者调整顺序所用的工具

Last in First out(LIFO)后进先出

只能对栈顶进行操作

Objects：A finite ordered list

Operations:

Judge Empty:

Stack:

Dispose:

MakeEmpty:

Push: give a new element in

Top: look at the top element

Pop: take out the top element and delete it

Implementation

• Linked List(with a header): from top to down

用链表实现时 链表的第一个元素位于stack的top

head可以理解为stack外的一块内存，s是head的名字，就是这个head块 起到定位作用（地址）

s->next = first element in stack

//push:
  Tem->next = s->next
  s->next = Tem
//top
  return s->next->element
//pop:
  first = s->next//确定第一块的位置
  s->next = s->next->next
  free(first)

But malloc and free are expensive

Solution: use a recycle bin

• Array: much better when knowing size

struct Stack
{
  int Capacity;//size
  int Topofstack;//the top pointer's location

  //此处的pointer 不仅仅指c的pointer，是一个储存地址的符号，也可以是下标等等
  //只要存放的是 位置 都可以是指针
  ElementType *Array;//category of element
};

添加元素时top++，删除元素时top--，指针向下移动，但是只是数值减小，并不会free上方的元素，只是当作他们不存在

eg: Balancing Symbols check if () and [] and {} are balanced

从左到右一直看左括号，遇见的第一个右括号一定是和左括号匹配的，此时删除这一对括号，接着继续重复的操作，读完整个输入，如果栈内为空，则balance

Algorithm
{
  Stack S;
  InitializeStack(S);
  while (more input)
  {
    read a character c;
    if (c is an opening symbol)
      push(c, S);
    else if (c is a closing symbol)
      if (StackIsEmpty(S))
        return (unbalanced);
      else
      {
        t = top(S);
        pop(S);
        if (t does not match the corresponding opening symbol of c)
          return (unbalanced);
      }
  }
  if (StackIsEmpty(S))
    return (balanced);
  else
    return (unbalanced);
}

eg：Postfix Expression a+b-cd = ab+cd- a(b+c)/d = abc+d/

Method:

• when meeting oprand, push into stack
• when meeting operator, pop two oprand and calculate, then push the result into stack

solution to () never pop a ( until you meet a )

eg: Function calls: system stack

stack pointer: to the top of the stack

function pointer: to the bottom of the current function frame

infix to postfix

输入一段中缀表达式，转换到后缀表达式

遇见operands直接输出，遇见operators先放进栈内，继续输出数字，遇见下一个表达式时，比较两个表达式的优先级：

1. 栈内的大于等于栈外的，pop栈内的，与栈内下一个进行比较

2. 栈外的大于栈内的，继续push

3. 遇见括号：

栈外的括号优先级最高，直接进入，遇见有括号时弹出括号往上的所有operators，改变括号优先级方法：

1. 用条件判断
2. 设置两套括号，栈内一套，栈外一套

Queue ADT

保持顺序使用

First in First out(FIFO)

Objects: A finite ordered list

Operations: ...

Enqueue: add a new element to the end of the queue

Front: take out the first element

Dequeue: take out the first element

Implementation

• Array

struct QueueRecord
{
  int Capacity;// max size
  int Front;// the first element
  int Rear;// the last element
  int Size;// current size
  ElementType *Array;
};

• Circular Array

Note: To defferentiate the empty and full, we need to waste one space, which means the max size is n-1

Another method is to use a flag to indicate the empty and full

Lec 06 Tree

A collection of nodes.

Consists:

1. a distinguished node r, called root
2. and zero or more nonempty (sub)tree

• subtrees must not connect together
• there are N -1 edge with N nodes

degree:

the numbers of subtrees of a node

degree of a tree is max of all degrees

children:

directly connected ones(not all descents)

siblings:

children of the same parent

leaf:

degree 0 node

path:

a unique sequence of nodes

length:

the edges number

depth:

length of the unique path from the root

Implementation

1. first child next sibling

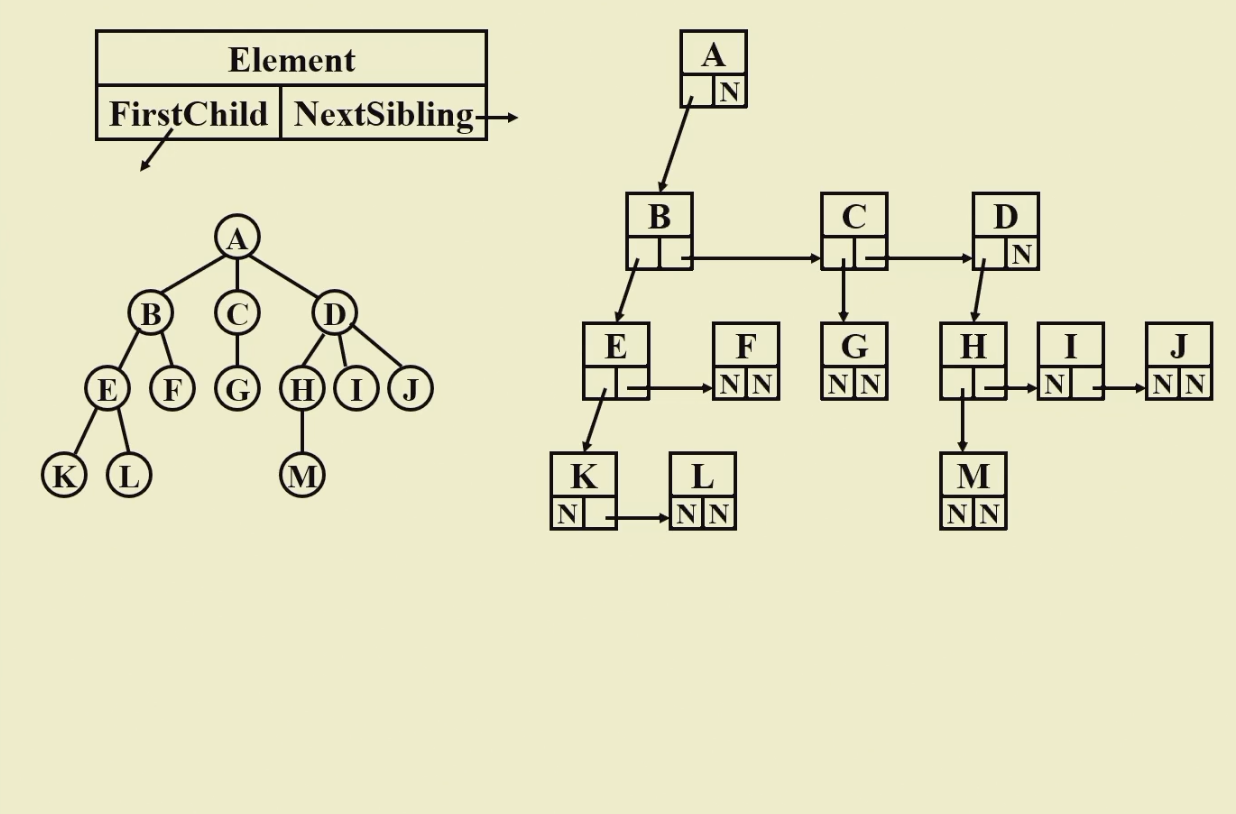
1. binary tree

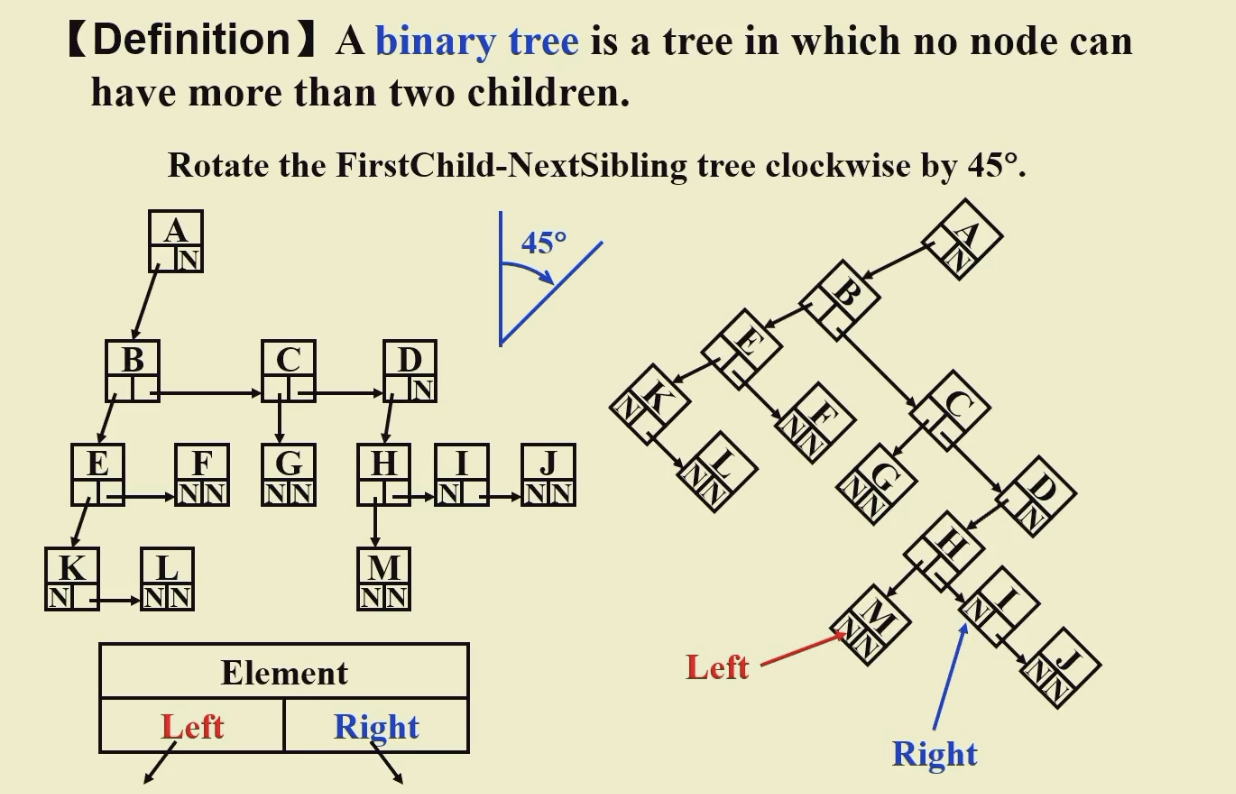
eg

• expression tree:

先进行中缀表达式转后缀表达式：

利用堆栈递归实现：

对后缀表达式遇见operand push，遇见operator pop出栈内的两个元素形成一个树，再将这个树的root push进堆栈作为后续形成树的元素

-->栈内的元素就是tree

• tree traversal:

采用递归的方式，可以preorder 也可以postorder

preorder：先操作再递归

postorder：先递归再操作

除此之外：层序遍历 level order：

用queue实现

将每一层的node全部输出后进入下一层

1. 当前层元素全部enqueue
2. queue不为空时：
3. dequeue一个元素
4. enqueue这个元素的node

void levelorder(tree){
enqueue(tree)
    while(queue is not empty){
        visit(T = dequeue())
        for(each child C of T)
            enqueue(C)
    }
}

inorder(only in binary tree)

先左后右递归

for binary inorder:

void inorder(tree){
  if Node == NULL
    return;
  inorder(tree->left);
    printf tree->data;
  inorder(tree->right);
}

• file structure

1. 按照层级tab

采用preorder，void fun(tree, depth)

传入两个参数，一个是当前树，一个是深度，每层递归时，深度加一，根据深度tab

Lec 07 BST

Properties of BT

层数为n的BT 最多有2^n-1个node

degree 为 0 （叶子结点）个数 = degree 为 2节点个数 + 1

proof：

n = n0 + n1 + n2

side = 2*n2 + n1

side = n - 1

可以消去n1

BST binary search tree

def：

1. 左子树数值一定小于根结点，右子树一定大于根结点（当前树的）
2. 左右子树都是BST！！！！

适用于：动态查找

通过中序遍历由小到大输出

Implementation

1. find

递归实现：

basecase：T = NULL

左边 else 右边 else 本身就是根结点数值

与树的深度成正比

2. find min max

递归向左右边走

3. Insert

4. check if k in

5. 看左右还有吗 没有就插

   tree insert(element x, BST t){
     if(t == NULL){
       T = ()malloc(sizeof(struct Treenode));
       T->element = x;
       T-left = T->Right = NULL;
     }
     else{
       if(T->element > x){
         t->Left = insert(x, t->Left);
       }
       else{
         t->right = insert(x,t->right);
       }
     }
     return t
   }
   

6. delete

7. delete a leaf: make its parent point to NULL

8. n1: replace it by its single child, and free it
9. n2:

尽量保证原来树的结构：用替换的方法

选左边最大的元素或者右边最小的元素放到删除位置，再将用来替换的元素

tree delete(element x, BST t){
  position tmpcell
  if(t == NULL)
    return not found;
  else if(x < t->element)
    t->right = delete(x, t->right);
  else if(x > t->element)
    t->left = delete(x, t->left)//search for the position
   else{
     if(t->left && t->left){//if n2
       tmpcell = findmin(t->right);//use find a min on right way
       t->element = tmpcell->element;
       t->right = delete(t->element, t->right);
     }
     else{// if n0 or n1
       tmpcell = t;
       if(t->left == NULL)
         t = t->right;
       else if(t->right == NULL)
         t = t->left;
       free(tmpcell);
     } 
   }
  return t;//return t to its parent 
}

lazy deletion: don't free a node but add a flag to it

Lec 08 Priority Queue(Heaps)

delete the element with the highest / lowest priority

Binary Heap

1. Structure Property

完全二叉树：

保证树高h=logn

是部分的完美二叉树-->完全三角形且节点的标号是完全按照顺序的

适合用数组存放（完全利用空间）

用数组进行存储：

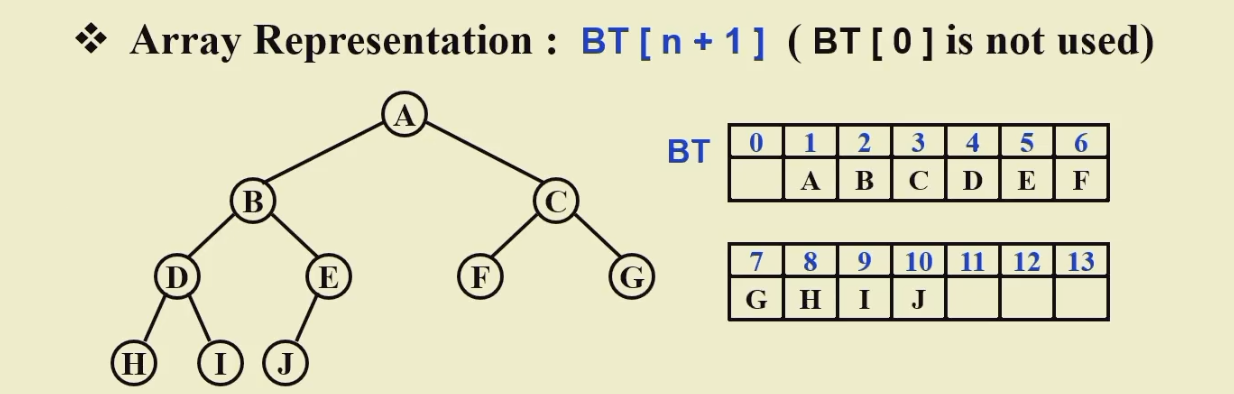
不会有空间浪费（无偏斜树）

从index = 1 开始存储

index = 0 的位置作为哨兵，设置成离开数值范围的值

• 运动方式：以数组角标1开始

-->下标x2 向左走

-->下标x2 + 1向右走

从下往上走：➗2 取整

2. Order Property

To def min heap and max heap:

​ 直属的大小关系分别为递增/递减，比较兄弟不一定，沿路径单调，因此搜索任意值一定要全部扫描，所以HEAP不适用于搜索（BST更好）

​ 但是root一定是最值，所以适合对最值操作

### Operation

1. Insertion: 上滤

假设放在最末尾—>判断(与parent大小)是否成立

void Insertion(data x, Queue H){
 int i;
  if(isFull) Error;
  for(i = ++H->size; H->element[i/2] > x; i = i/2){// 总会有哨兵使之停止                    //与parent比较大小
    H->element[i] = H->element[i/2];//上滤找位置 非交换
        ^
        |
//在这里第一次操作相当于加入一个新单元 因为i = size是边界，++size是新的空间
  }
  H->element[i] = x;
}

O(logn)

2. Delete min：下滤

包括拿出最小值和重构Heap

重构：取出最后一位的数据，下滤（由root位）找到可以放他的地方

int Deletemin(Heap H){
  int i, child;
  1.判空；
  minelement = H->element[1];
  lastelement = H->element[H->size--];//暂时取出最后一位元素
  for(i = 1; i*2 <= H->size; i = child){//下滤过程
    child = i*2;
    if(child != H->size && [child+1] < [child])
      child ++;//暂存的最后一个元素要满足property：需要小于两个孩子中最小的那个
    if(lastelement > [child])
       [i] = [child];//下滤
    else break;//找到位置，break
  }
  [i] = lastelement;
  return minelement;
}

3. Decrease/Increase Key:

调整优先级，将任务上浮或下沉，Key是某个任务的优先级顺序，改变Key的大小

需要重新调整堆使其保持特性

void DecreaseKey(int i, int value, Heap *h){
    int j;
    if(i > h->size){
        printf("Index is not in the heap\n");
        return;
    }
    if(h->element[i] < value){
        printf("New value is greater than current value\n");
        return;
    }
    for(j = i; h->element[j/2] > value; j/=2){
        h->element[j] = h->element[j/2];
    }
    h->element[j] = value;
}

4. Delete：

先Decrease 再 Deletemin

5. build Heap

void BuildHeap(Array H[]){
  int i = h->size/2;
    for(; i > 0; i--){
        int j = i;
        int tmp = h->element[j];
        int k = j*2;
        while(k <= h->size){
            if(k < h->size && h->element[k] > h->element[k+1]){
                k++;
            }
            if(tmp > h->element[k]){
                h->element[j] = h->element[k];
                j = k;
                k = j*2;
            }else{
                break;
            }
        }
        h->element[j] = tmp;
}

Lec 09 Disjoint set

等价关系 equivalent relation

symmetric reflexive transitive

等价类： 具有相同等价关系的一类对象

• eg：对等价类进行分类

void find(){//并查集算法
//1.read in relaitions
Initial n disjoint set;
  while(read in a~b){
    if(!(Find(a) == Find(b))){//如果两者不属于同一家族，
      Union two set//合并这两个家族
    }
  }
//2.dicide if a~b
    while(read in a and b)
    if(Find(a) == Find(b)) output(true);
    else output(false)
}

Implementation

用数组，但实际上是指针

Union

S[element] = element's parent

S[root] = 0 and

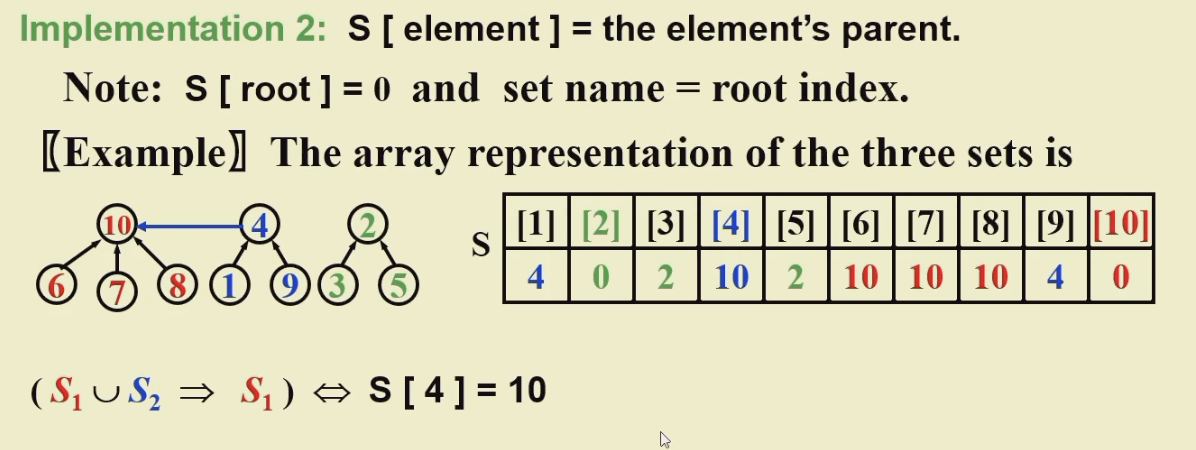
Find

for(;S[x] > 0; x = S[x])
  return x;

但是会有可能成为线性链表，树高非常高

Smart Union

1. union by size

存放size：S[root] = -size

此时的size不会超过log2(N)+1

Path compression

type find(s, x){
    if(S[x] <= 0) return x;
  else return S[x] = find(S[x], S);//递归的将经过节点连到father 从而达到path compress
}

非尾递归，会在每次递归的时侯将经过的节点连到father上

Lec10 Graph Algorithm

一个挨着一个->线性表

一个管好多个->树

树是图的特殊情况

图是多对多

Def

G(V, E) 顶点 边

可以只有顶点没有边，至少有一个顶点

• 无向图 undirected

(v1, v2)

• 有向图 directed

< v1, v2 >

complete graph : a graph has max edges

边数：有向n*(n-1)

​ 无向n*(n-1)/2

adjacent:相邻的

对有向图：A->B: A is adjacent to B, B is adjacent from A

subgraph: 顶点的子集&&边的子集

path:(v1, v2,......)

length of path: 边的数量

simple path：每个v不相等

circle: simple path with vi = vj 头尾相等的simple path

connected graph: every pair of v is connected

Component: 一个图里的最大连通子图(不能再加入一个v/e， 否则就不相连)

tree: 无环的根结点为一的图

DAG: 有向无环图

Strongly connected directed graph: 任意一对顶点，往返都有路

Weakly connected: 不满足强连通，但是将其转变为无向图后连通的图

Degree: 入度+出度Degree: number of edges incident to v. 2E=∑degree

Representation

• 二维数组

adj_set[ i ] [ j ] = 1 if i j connected else = 0

• 链表

只存出度

n个顶点，要开一个长度为n的一维数组，对应位置是每个顶点

数组元素是链表的头指针，即相当于开n个链表的头指针，存储时：

A->B：找A链表，将B的头节点插入到A的链表中

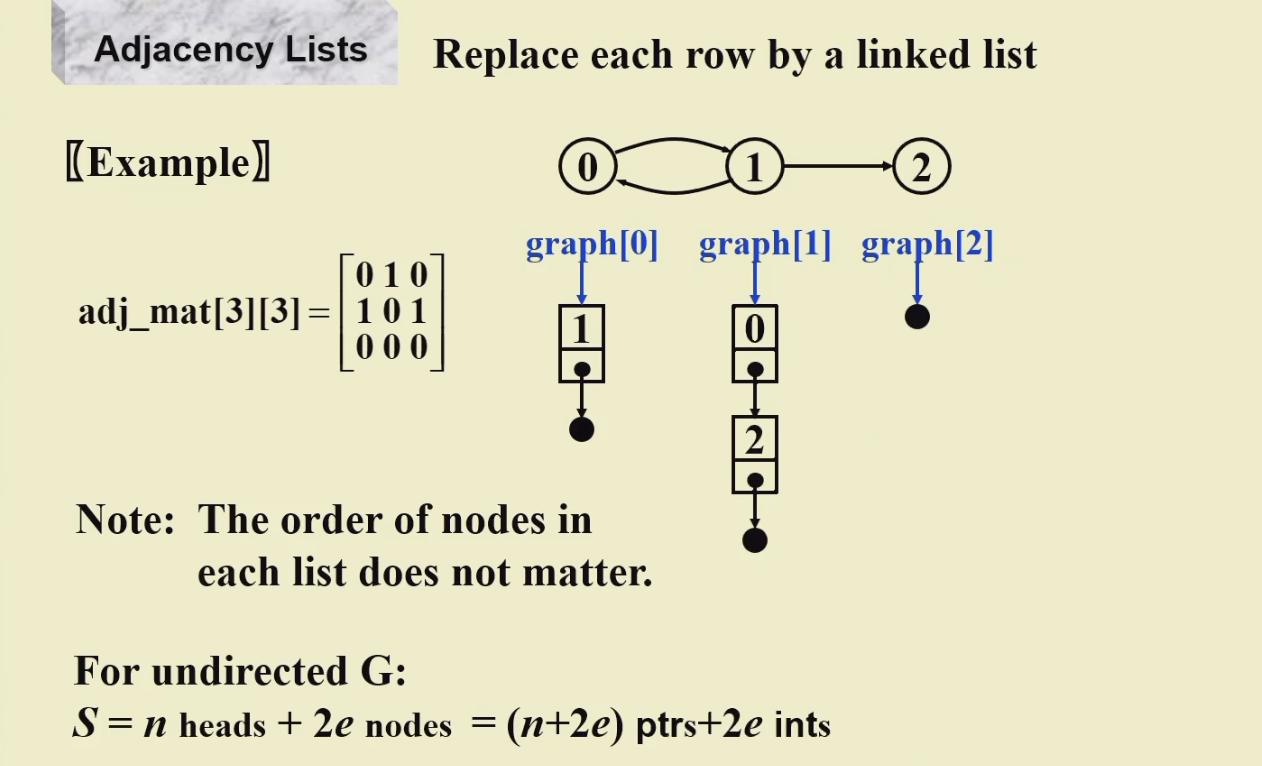
• Multilist

存边，结构体里包含mark，用于标记这条路是非被访问过，两个点指向所连接的节点

1. 拓扑排序

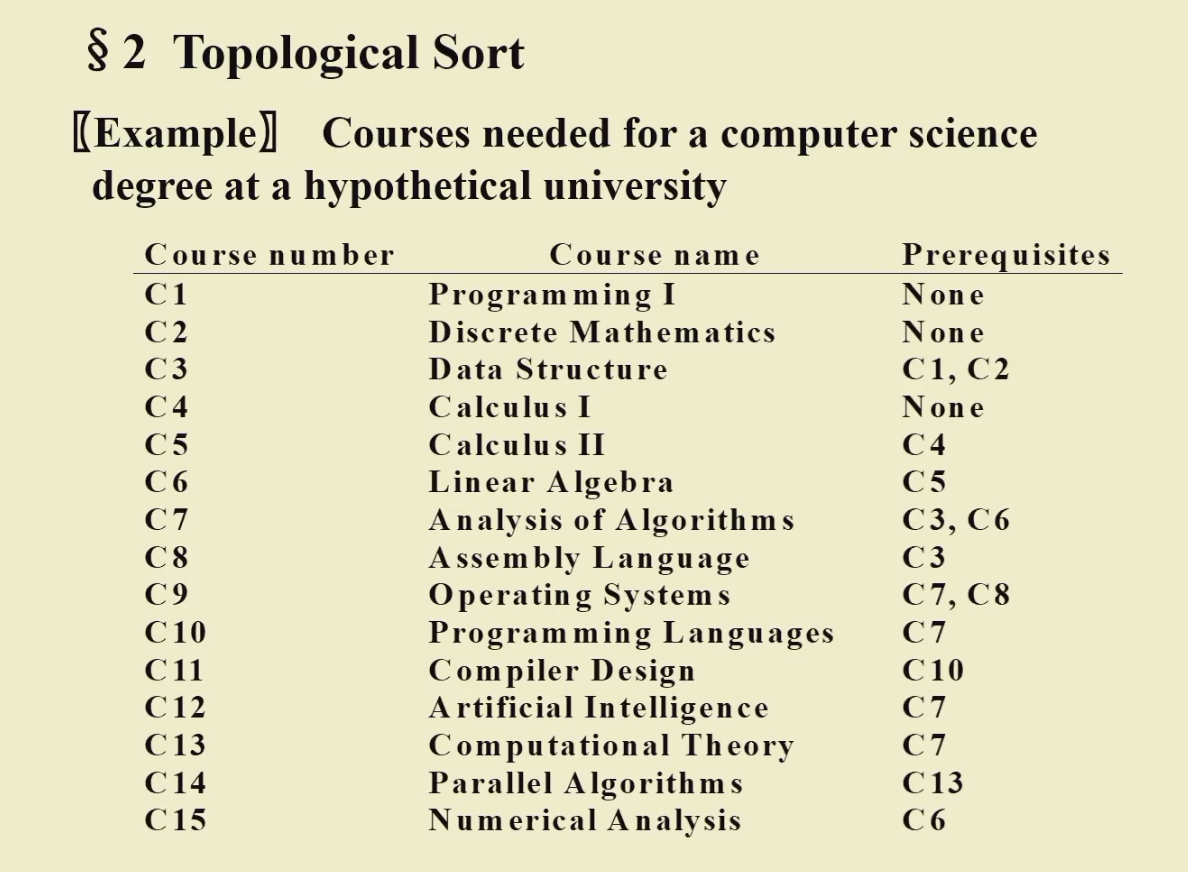
AOV Network activity on verticle

一定是非自反的-> DAG

拓扑序：

理解：按照所有的先修课都不冲突的情况能排出一个课表

void Toposort(Graph G){
  int counter;
  Vertex v, w;
  for(counter = 0; counter < Numvertex; counter ++){
    v = findNewVertexofDegreeZero();//找到一个入度为0的边
    if(v == NotAVertex){
      Error("Graph is a cycle"); break;
    }
    TopNum[v] = counter;//如果有可以学的课，将它学掉
    for(each w adjacent from v)
      indegree[w]--;//并且将以它为预修课的课中删掉（减小他的下一门课的入度）
  }
}//O(v^2)

改进：采用一个结构存储入度为0的节点

Lec11 Shortest Path Algorithm

两点之间的权重和最小->weighted path length 最小值

1. single-source 单源最短路

固定一个顶点到其他点的（加权）距离最小

• 无权：等价与每条路的权重是1

Breadth-first Search: 固定一个点 找与他距离为1的点

过程中标记避免走重复路经

存储路径：用父指针记录前一个位置 存前置顶点的编号

void Unweighted(Table T){//T is initialized with source vertex S
  queue q;
  vertex v, w;
  q = CreateQueue(NumVer); MakeEmpty(q);
  Enqueue(S, q);//初始化时将起点进队列
  while(!IsEmpty(q)){
    v = Dequeue(q);//将当前节点推出队列
    T[v].Known = true;//tag the vertex which has been visited，这一步可以不要
    for(each w adjacent from v){
      if(T[w].Dist == infinity){//如果这个位置没有被访问
        T[w].Dist = T[v].Dist + 1;//记录下一个节点的距离
        T[w].Path = v;//记录下一个节点的路径
        Enqueue(w, q);//将邻近的节点作为下一个当前位置
      }
    }
  }
  DisposeQueue(q);
}

O(V+E): 每次进入一个V 走遍V

• 有权：

Dajkstra

void Dijkstra(Table T){
  for(;;){
    v = smallest unknown distance vertex;
    T[v].known = true;
    for(each w adjacent to v){
      if(T[w].known == false){
        if(T[v].distance + Cvw < T[w].distance){
          T[w].distance = T[v].distance + Cvw;
          T[w].path = v;
        }
      }
    }
  }
}

Lec 12 Network Flow & Minimum Spanning Tree

Network Flow

Network 有权

Flow 有向

由source 到sink 源到汇

将每个边的大小当作管道的最大流量

The task is to find the maximum amount of flow that can pass from s to t

1. undo

找到一条路上最大通量，将这条路上的每条边减去这个值，并在每条路上反向加一个这个值

时间复杂度：O(fE) f是最大流

Minimum spanning tree

一个子图包含所有顶点，包含一部分边，构成了一个树

use greedy:

1. use only edges within graph
2. use exactly V-1 edges
3. no use edges that produce cycle

Prim : grow a tree

类似Dijkatra 因为生成树需要n个点，每一步都是子生成树

开始选择一个点，找邻边最小的作为第二个点，此时就有了一个子生成树，接下来每一步都需要选择这个子树的向外扩展边（边的一头在树上，一头不在）

Kruskal : maintain a forest

以边的角度考虑，每次找最小的边，同时保证不构成回路，这样选完n-1条边后，就会有一个最小生成树

void Kruskal(Graph g){
  T = {};//set as empty
  while(|T| < V-1 edges && E is not empty){
    choose a least cost edges(v, w) from E;
    delete it from E;
    if((v, w) wont cause a cycle)
      add(v, w) to T;
    else
      discard it;
  }
}

适用于

可以用堆找到最小值

判断是否构成回路：并查集算法，每次找边的时候相当于加入一个等价关系

时间复杂度：O()

Lec 13 BFS DFS

图相关问题的本质是遍历

将二维结构转化成一维结构去做

遍历时：需要选定一个基准位置，在基准位置上找相连接的各个点

在这个过程中，每次只能选择一个相邻点，剩下的点需要保存

-->根据保存方法分类：

1. 用队列：宽度搜索
2. 用堆栈：深度搜索 但是程序实现时通常用递归而不用堆栈

DFS

1. undirected

void DFS(Vertex a){
  visited[a] = true;
  for(each w adjacent to v){
    if(!visited[w]){
      DFS(w);
      printf("\n");
    }
  }
}

计算连通分量：对一个图进行遍历后查看visited 如果没有visited，调用DFS 分量= DFS调用次数

双联通：拿掉图中一个点，剩余的图仍然是联通的

拿掉后图不连通 称这个点：关节点articulation

双联通则无关节点

双联通分量：最大子双联通图

Q1:计算双联通分量

1. 深度遍历 遍历时给每个节点添加Num作为遍历的顺序
2. 计算Low值：Low的理解：我能联络到的最高层（最小的num）
3. 查看满足关节的条件

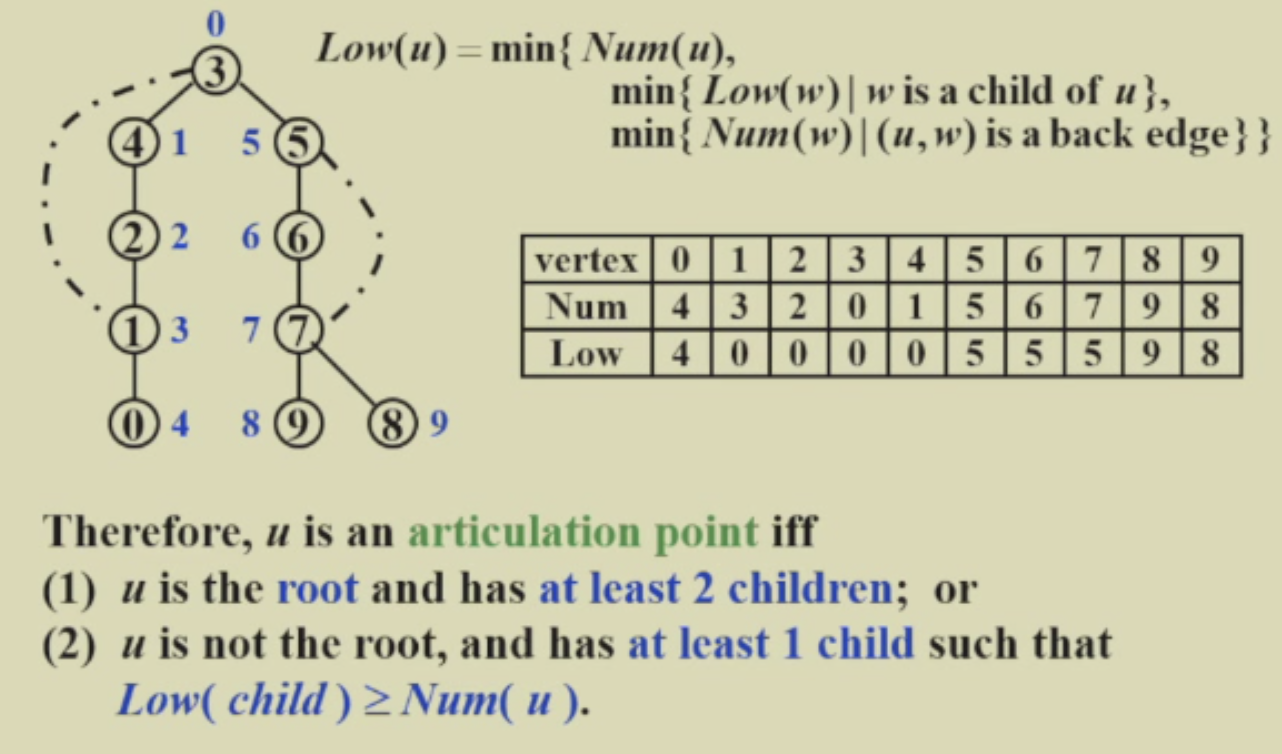
Q2:Euler Circuit

一笔画

结论：

1. 如果所有节点的度都是偶数，那么一定有欧拉回路Euler Circuit（起止点相同）
2. 如果有两个奇数度节点，可以形成欧拉路径Euler Tour（一笔画但不用起止点相同）

时间复杂度：O(E + V)

Lec 14 Sorting

selection

bubble

insertion

void insertion(int a[], int n){
  int tmp;
  for(int p = 1; p < n; p++){
    tmp = a[p];
    for(int j = p; j > 0 && a[j-1] > tmp; j--)
      a[j] = a[j-1];//移位
    a[j] = tmp;
  }
}//平均O(n^2) 有序时最好O(n) 无序时O(n^2)

Inversion 逆序：大小与位置不匹配的两项

最坏的情况：C(2 n)个逆序 需要交换C(2 n)次

平均：n^2/4

Shellsort

分组使用插入

最坏n^(3/4) 平均 n^(6/7)

Heap sort

树形选择

1. 首先建堆 重复去除堆顶元素 O(nlongn)

2. 建最大堆，每次将堆顶放到数组最后端，然后维护这个堆

2NlogN-O(NloglogN)

快排和merge本质上是一种思想：divede and conquer and merge

但是侧重点不同：

1. merge在二分数组后强调在分治之后的归并，但是归并的时候若左边已经全部小于右边，则无需merge 这就是快排的目标
2. 快排强调在divide时找到基准元素pivot 使得分治的数组整个都大于或小于

Merge sort

O(nlogn)

Quick sort

slower than insertion when N <= 20

选择pivot：可以前中后三个里面取适中的

一定是适中的：随机选五个 中间的元素

hqm的qsort：

Lec 16 Hashing

均匀

哈希函数怎么设计

冲突怎么解决

哈希方法的评价

Hashing for searching

通过计算来找对象

• 字典问题

ADT

< name, attribute >

hash table:

n 是实际进入的哈希元素 T是可提供的不同哈希值

identifier density: n/T

loading density: n/sb sb是哈希表的面积（可以存放的数量）

Design Hash

数字：

1. 求余法 u(x) = x%m
2. 平方取中：

将数平方，取中间的两位数

3. 折叠法：
4. 数字分析法

字符串：先变为数字

通过位运算进行转换：

int index_hash(char *x, int tablesize){
  unsigned int hashval = 0;
  while(*x != '\0')
    hashval = (hashval << 5) + *x++;//相当于 x 32
  return hashval % tablesize;
}

Collision

1. 链表解决：n个元素，哈希表至少长度为2n

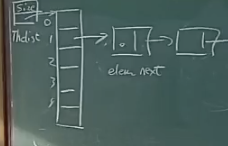
O(1) insertion

2. open addressing:

（H(x) + f(i) ）% Tablesize

i是冲突次数，f表示偏移量，典型的是f(i) = i, 称为

• 线性探测probing

平均成功查找次数：枚举法

平均不成功查找次数：根据哈希值的特点分类 对每类求平均值

• 二次探测：

f(i) = i^2避免初始聚集，但是有时候会找不到空位

在下列条件满足时，一定可以找到位置：

半满，TS = 素数

• double hashing:

将f(i)设计为新的i*H2(x)

典型：H2 = R-(x%R)

• rehash

将表扩大一倍后找最近的素数

rehash条件：

1. 元素超过一半
2. 超过load
3. 插入失败

评论区

欢迎在下方留言~