Intro¶

约 1497 个字 32 行代码预计阅读时间 5 分钟

Dealing with HARD problems

目标：得到一个近似解

Approximation Ratio¶

我们通过近似比\(\rho(n)\)来衡量近似算法的好坏，称一个算法是\(\rho(n)\)-近似算法。它的意义是：规模为n的输入下，近似解\(C\)与最优解\(C^*\)的比值，也就是说

\[ max(\frac{C}{C^*}, \frac{C^*}{C}) \leq \rho(n) \]

算法的近似比与问题规模相关，通常情况下\(\rho(n)\)随着n的增大而增大

Approximation Scheme¶

最优解的近似方案(Approximation Scheme)，指的是一类近似算法，对给定\(\epsilon > 0\)，它是一个(1+\(\epsilon\))近似算法

多项式时间近似方案（PTAS）：对于任意给定\(\epsilon > 0\)，能在多项式时间复杂度完成计算，记作\(O(n^{f(\frac{1}{\epsilon})})\)
- 完全多项式时间近似方案（FPTAS）：对于任意给定\(\epsilon > 0\)，能在多项式时间复杂度完成计算，记作\(O\left(n^{O(1)}\left(\frac{1}{\varepsilon}\right)^{O(1)}\right)\)

设计算法时，考虑如下三个方面：

最优性（Optimality）：解的质量
效率（Efficiency）：计算成本
全部实例（All instances）：通用性

对这几个方面进行trade-off

A+B：对于特殊情况的精准快速算法
A+C：针对全部实例的精准算法
B+C：近似算法

Example¶

Bin Packing¶

3 Solutions

Next fitFirst fitBest fit

Next fit：按照输入顺序一个个放物品，如果当前物品能够放在与上一个物品相同的箱子中，放入，否则新开

void NextFit() {
read item1;
while (read item2) {
    if (item2 can be packed in the same bin as item1)
        place item2 in the bin;
    else
        create a new bin for item2;
    item1 = item2;
} // end-while
}

时间复杂度为\(O(n)\)

可以得到一个近似比为2的解

First fit：按照输入顺序一个个放物品，如果当前物品能够放在当前任意一个箱子中，放入，否则新开

void FirstFit() {
while (read item) {
    scan for the first bin that is large enough for item;
    if (found)
    place item in that bin;
else
    create a new bin for item;
    } // end-while
}

时间复杂度为\(O(nlogn)\)

可以得到近似比为1.7的解

Best fit：按照输入顺序一个个放物品，当前物品需要放在剩余空间最小的箱子中，如果不存在，则新开

时间复杂度为\(O(nlogn)\)

可以得到近似比大于1.7的解

Failure

不用太多考虑边界情况：因为最坏情况下special case 不会太多

On-line Algorithm

装箱问题中是在线算法，并且没有回溯，这样是很难对抗数据分布的——因为看不到数据的整体情况

Failure

对于所有在线算法，装箱问题都到不了\(\frac{5}{3}\)这个近似比

Off-line Algorithm

在离线算法中，我们可以得到如下结论：令\(M\)为桶的个数，则：

\[M \leq \frac{11}{9}OPT + 6\]

使用First fit Decreasing 算法，即先对物品按大小降序排列，再使用First fit算法，则有

\[FFD(L) \leq \frac{3}{2}OPT(L)\]

Knapsack Problem¶

小数背包¶

Question

令背包容量为\(M\)，给定\(n\)个物品，每个物品\(i\)有重量\(w_i\)和价值\(p_i\)，被放进背包的比例不超过\(x_i\)，此时该物品的价值为\(p_i x_i\)，目标是令\(\sum_{i=1}^{n} p_i x_i\)最大

解决方法是每次按照价值密度：\(\frac{p_i}{w_i}\)降序排列，然后贪心选择

0-1 背包¶

在先前我们使用的贪心算法这里就不一定会得到最优解，因此那个贪心算法就是一个近似算法，下面对其近似比\(2\)进行证明：

证明

显然：所有物品中价值最大的一个物品的价值肯定小于最优解的总价值，也小于小数背包的最优解

\[ p_{max} \leq P_{opt} \leq P_{frac} \]

并且：最大价值物品的价值小于贪心解的总价值（可以反证来理解最大价值物品一定会被贪心选择，当然这里假设每个物品的大小都小于背包大小）

\[ p_{max} \leq P_{greedy} \]

还有一个式子：

\[ P_{opt} \leq P_{greedy} + p_{max} \]

这是因为一个前提：在小数解中，其实只会有一个物品被拆分放入，也就是说贪心解和小数解的差值就是没有被拆分放入背包的物品的价值，这个物品肯定是放入背包的物品中的价值最小的一个，在这里进行放缩，将这个拆分的物品价值替换为价值最大的物品，这时\(P_{greedy} + p_{max}\)一定大于\(P_{frac}\)，进而大于\(P_{opt}\)

对这个式子除以\(P_{greedy}\)，得到：

\[ P_{opt} \leq 2P_{greedy} \]

K-Center Problem¶

K-Center Problem

给定\(n\)个点，在地图上选择\(k\)个点，使得所有点到最近的中心点的距离最小

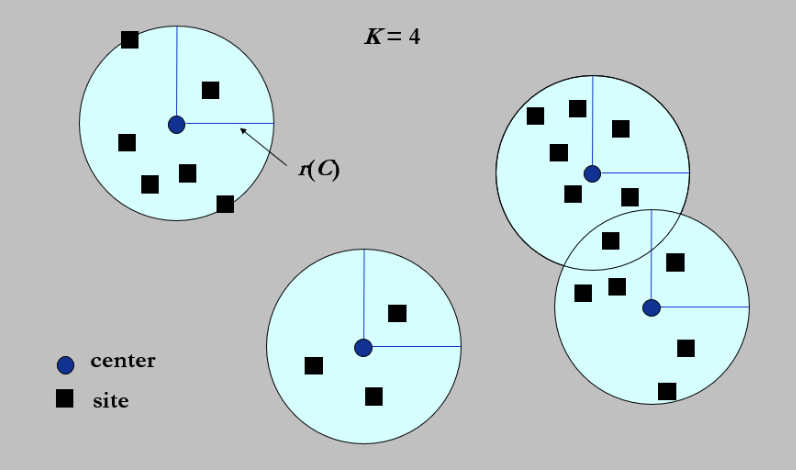
这里运用贪心算法解决问题

让第一个点选择为所有点的中点：显然不行，如果有两坨点离得很远那这个点就非常不合适
随机选取算法：

引理

在改进的贪心算法中，我们直接挑选某个地址作为中心点。这种做法之所以可行，是因为某个中心点覆盖半径为r的区域，可以近似为以（接近）区域边界上一点s为新的中心点，2r为半径的区域。虽然这个区域明显比原区域大，但它保证能够覆盖原区域所能覆盖的点。这样的话我们就不必通过繁琐的计算算出中心点，而是从原有的地址中选择中心点，方便了很多。

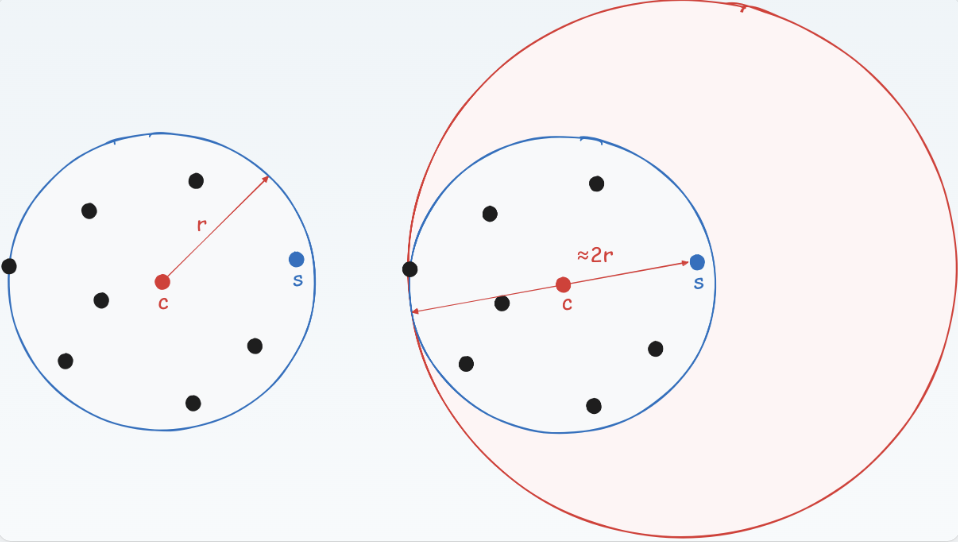
从输入点中随机选取一个点作为第一个中心，然后删除该点为中心，\(2r\)为半径的所有点
- 这里的参数\(r\)可以通过二分查找来计算，先令\(r = \frac{max(d(i,j))}{2}\)，然后检查是否满足条件，如果满足则缩小\(r\)，否则增大\(r\)
- 时间复杂度为\(O(logr_{max})\)
在剩余的点中继续选择第二个中心，以此类推

如果一个值\(r\)是最优的，那么这一算法得到的解是最优解的两倍——即这是一个\(\rho(n) = 2\)的近似算法

Centers Greedy-2r(Sites S[], int n, int K, double r) {
    Sites S`[] = S[];  // S` is the set of the remaining sites
    Centers C[] = NULL;
    while (S`[] != NULL) {
        Select any s form S` and add it to C;
        Delete all s` from S` that are at dist(s`, s) <= 2r;
    } // end-while
    if (|C| <= K) 
        return C;
    else
        ERROR("No set of K centers with covering radius at most r");
}

评论区

欢迎在下方留言~