External Sort¶
约 1628 个字 16 张图片 预计阅读时间 5 分钟
数据没有办法全部加载到内存中,我们需要用硬盘存储,今天的模型基于硬盘与内存之间的数据传输
Intro¶
今天的模型:external memory model
在这个model中,我们有一个CPU,一个Internal Memory,with \(M\) cells(每个cell可以存储一个item),一个External Memory(disk),由若干条磁带(tape)组成:
- infinite length
- 只支持sequential access,只能从前往后读
-
CPU对数据进行处理,需要将数据从disk读到memory,然后进行处理,处理完后再将数据写回disk,这个过程称为I/O
- I/O过程以block为单位进行,每个block有\(B\)个item
- I/O cost:总共读写的block数
在这里:\(M\)和\(B\)是参数,并不是固定的,通常我们假设\(M \geq 3B\),并且输入规模\(N >> M\)
scan:
有\(N\)个item,需要扫描所有item
这时的cost = \(O(N/B)\),我们称这个cost为linear cost(而不是\(O(N)\)),一次这样的扫描称为一个pass
Sorting¶
采用merge sort的思路进行,但是是对disk的操作方法:
下面是一个\(M=3, B=1\)的例子:
Example
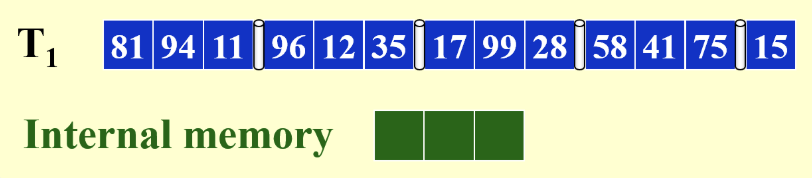
- 我们的比较并交换操作是在memory中进行的
- 磁带只能完成顺序读写操作
步骤:
- 将第一个block从磁带读到memory中并完成排序
- 将排好后的block暂存到tape2中
- 将第二个block从磁带读到memory中并完成排序
-
将排好后的block暂存到tape3中
重复这个过程,直到磁带上的block全部读完
这样就完成了第一次pass,此时tape1中的数据按blcok排好了,交替放置在tape2和tape3中:
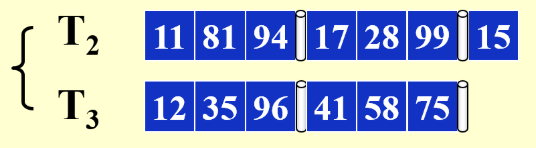
这里我们选择了两个磁带来交替存储内存输出的block结果,就是因为磁带只能顺序读写,在merge时就体现出来了
merge采用的思路是用内存作为比较器,将两个tape中对齐的block进行比较,谁小谁写入磁带,然后指针后移:
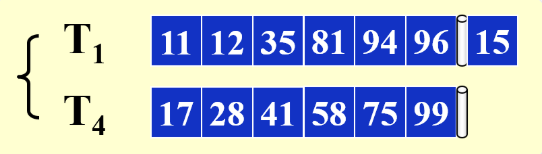
重复这个过程

再对上面这张图片的tape进行一次merge
在整个过程中,我们完成了1+3次pass:
- 1次pass:用memory完成block排序
- 3次pass:用磁带完成merge
推广
在输入规模为\(N\)时,我们每次在memory中完成一个block的排序,会输出一个run(一个有序的block),在将disk完全读好后,产生了了\(N/M\)个run,然后进行merge,每次merge减少一半的run,直到只剩下一个run为止,这样就得到了结果
因此总的I/O cost为:
怎样减少pass的次数?
K-way Merge¶
一个简单的思路是在merge时,增加磁带的个数,将原先的2个磁带改为\(k\)个磁带,这样每次merge时,run的数量除以\(k\),原先的\(log_2\)就变成了\(log_k\),这样就减少了pass的次数
理想情况下是像上面这样的,但是我们在进行merge时需要使用memory进行排序,因此还要考虑memory的限制:
在merge时,我们读入\(k\)个block,对block排好序后将结果存储到buffer中,然后写入磁带:

但是buffer满了后,需要将buffer中的数据写入磁带,这个过程很慢,为了不让排序停止,我们再留出一个buffer,作为I/O buffer,这个一边继续排序一边I/O:

k's limit
从上面的描述中,我们知道了至少需要k+2个block,由于我们最大只有\(M\)大小的memory,所以有不等式:
因此,\(k\)的最大值为\(M/B - 2\)
因此,k-way merge的pass次数为:
因此总的I/O cost为:
在这里可以看出,B越大时,每次的linear cost越小(做一次pass的cost变小),但是底数也会变小,导致后面的log变大(pass变多),因此这是一个trade-off
Replacement Selection¶
刚才的方式是通过每次合并多个run来减少pass次数,这里采用的方法是增长run的长度
在这里采用置换选择的方法来生成run(myc老师说这是一个很工程的方法,所以我也就直接通过例子写算法操作的步骤了)
例子
这里我们还是用M=3, B=1的例子

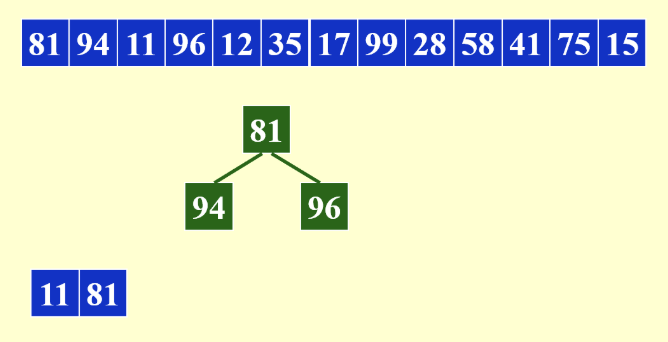
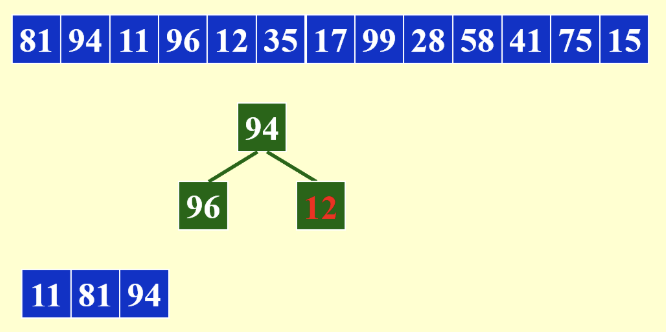
方法就是通过用内存生成一个最小堆,初始情况下将堆顶元素放入tape中,然后从堆中删除堆顶元素,读入新的元素:
- 如果新的元素小于tape中的末尾元素,新元素变红不再处理,同时维护堆
- 当堆中所有元素都为红时,结束当前run,开始下一个run
- 当所剩余的元素小于等于内存大小时,直接写入新的run
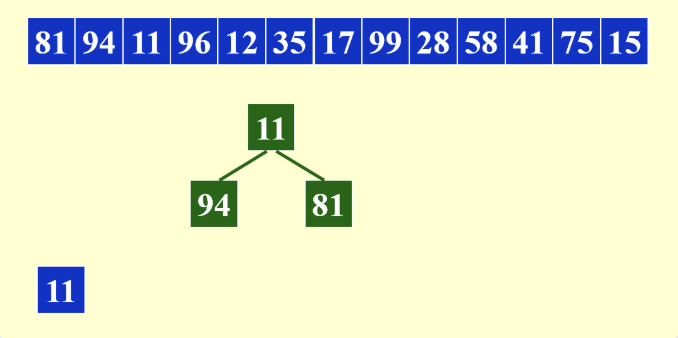
注意这里变红之后仍然是要做一次维护+推入的
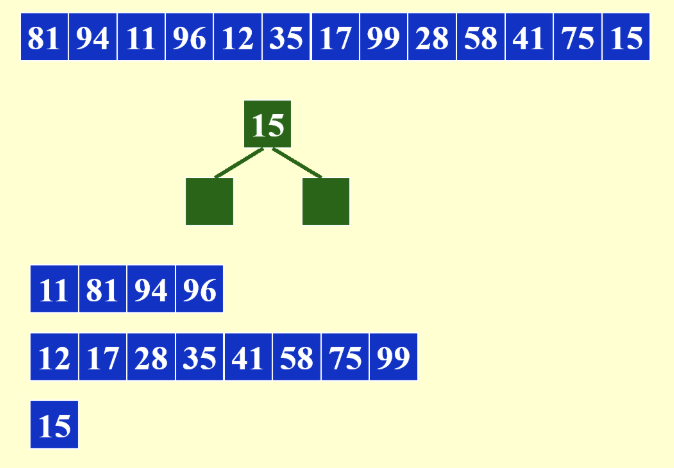
这个方法得到的平均意义的run长度为\(2M\),特别地,对于初始条件比较有序的数据,run会非常长
Reduce Merge Time¶
利用了一下离散数学中学习的huffman编码,先将较短的run进行合并
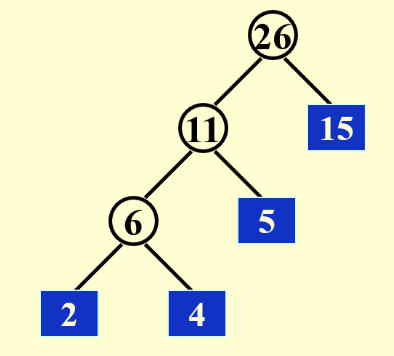
然后计算合并时长:
\((2+4)*3 + 5*2 + 15*1 = 39\)
原先的方法(k = 2)需要将每一个run都跑两遍,需要52
Polyphase Merge¶
刚刚说的k-way merge,需要2k个磁带
这里会讲解一种算法,使用k+1个磁带完成merge
在这里给出一个k=2的例子

规律总结:

推广到k=3时:

注意
这里可能有些不清晰,myc老师在上课时没有说明\(k > 2\)时初始情况的划分,我在钉钉问了一下:
我的问题是:像k=2时,我们通过对\(F_N\)的划分,得到了\(F_N = F_{N-1} + F_{N-2}\)并将其拆分成到了t2和t3中,那么k=3时,为什么拆分出来的结果加和不是\(F_N\)?
他的回答是:
在\(k>2\)时,我们的初始数量并不是\(F_N\),而是t1+t2+t3这些tape中的run之和(如果我们拥有的run的数量达不到这个数量,可以通过添加dummy run来实现)
这一点在接下来的任意数量推广中同样适用
推广到\(\forall k\):

留言