跳转至

Amortized Analysis

约 891 个字 -3 行代码 预计阅读时间 3 分钟

均摊法分析是对一系列操作的平均性能进行分析，而不是对单个操作的性能进行分析

bound介于worst和average之间且均摊界与概率无关

通常有三种方法：Aggregate Accounting Potential

Aggregate Method

对一系列的操作进行最坏时间情况分析得到\(T(n)\)，此时： $$ T(n) \leq \sum_{i=1}^{n} t_i=O(n) $$ 这时\(T(n)\)逼近于\(O(n)\)，即均摊时间复杂度为\(O(1)\) 但是这个方法的难点在于需要确定这个\(\sum_{i=1}^{n} t_i\)，也就是总的时间开销

在讲解其余的两个方法之前，yy哥说了一个很有趣的故事： yy在学校门口开了一个小卖部买汽水，每次卖出一瓶成本为1的汽水，学生至少要交一块钱，但是也可以多交钱存到下次使用，汽水的成本就是actual cost，而学生交的钱就是amortized cost，多出来的钱我们称作credit

Accounting Method

在这个方法中，我们自己设置均摊价值，但需要保证均摊价值不会小于实际价值，即：

\[ \sum \text{amortized cost} \geq \sum \text{actual cost} \]

(也就是不会赊账)

这时候就会得到一个实际价值的上界

这个方法的过程就是：

  • 首先分析实际价值
  • 然后设置均摊价值
  • 分析credit的值，确保其大于等于0

MultiPop

ads-5

Potential Method

直观的、一次性定义所有操作的均摊代价，对于某些大量操作需要定义均摊价值的情况，这种方法更加适用

\[ \hat{c}_i-c_i=\text { Credit }_i=\Phi\left(D_i\right)-\Phi\left(D_{i-1}\right) \]

解释：

\(Credit_i\)：第\(i\)次操作的credit，这时我们引入一个状态得分函数\(\Phi(D)\)，这个函数的值是一个状态的代价\(D_i\)是第\(i\)次操作后的状态

但是对于每一次操作，\(Credit_i\)的数值不仅由当前的状态决定，还受到之前状态的影响，因此我们用\(\Phi(D_i)-\Phi(D_{i-1})\)来表示

此时，我们可以得到：

\[ \sum_{i=1}^{n} \hat c_i=\sum_{i=1}^{n} c_i+\Phi(D_n)-\Phi(D_0) \]

恰好在这个求和的过程中，只留下了\(\Phi(D_0)\)和\(\Phi(D_n)\)，这两个值是常数，从而我们得到了\(\sum_{i=1}^{n} \hat c_i\)的值

实际操作中，我们：

设计势能函数

  • 选择一个合适的状态得分（势能）函数\(\Phi(D)\)
    • 势能函数的定义要求：\(\Phi(D_0)=0\)
  • 反应函数的潜在复杂度
  • 检查Credit合法性
  • 计算\(\sum_{i=1}^{n} \hat c_i\)
  • 最好的势能函数应该确保n次操作的credit值尽可能小

对Splay树进行均摊分析

若选深度作为势能函数，无法计算所有节点的深度变化，因此不能选择

若选择所选转节点的子节点个数，可以行得通，但是X、G的变化太大，所得到的界太松

最终选择的技巧是：

对节点数取对数 得到树的秩

即：\(\Phi(D)=Rank=\sum\log S(n)\)


对势能函数分析时，如果进行完全分析，需要对每个节点的credit进行计算，但是这样计算太复杂，因此我们进行放缩，只对所寻找的目标节点的势能进行分析，这样可以简化问题

需要用到下面的引理：

Lemma

\[ if:a+b \leq c \]
\[ then:\log a + \log b \leq 2\log c + 2 \]

ads-6

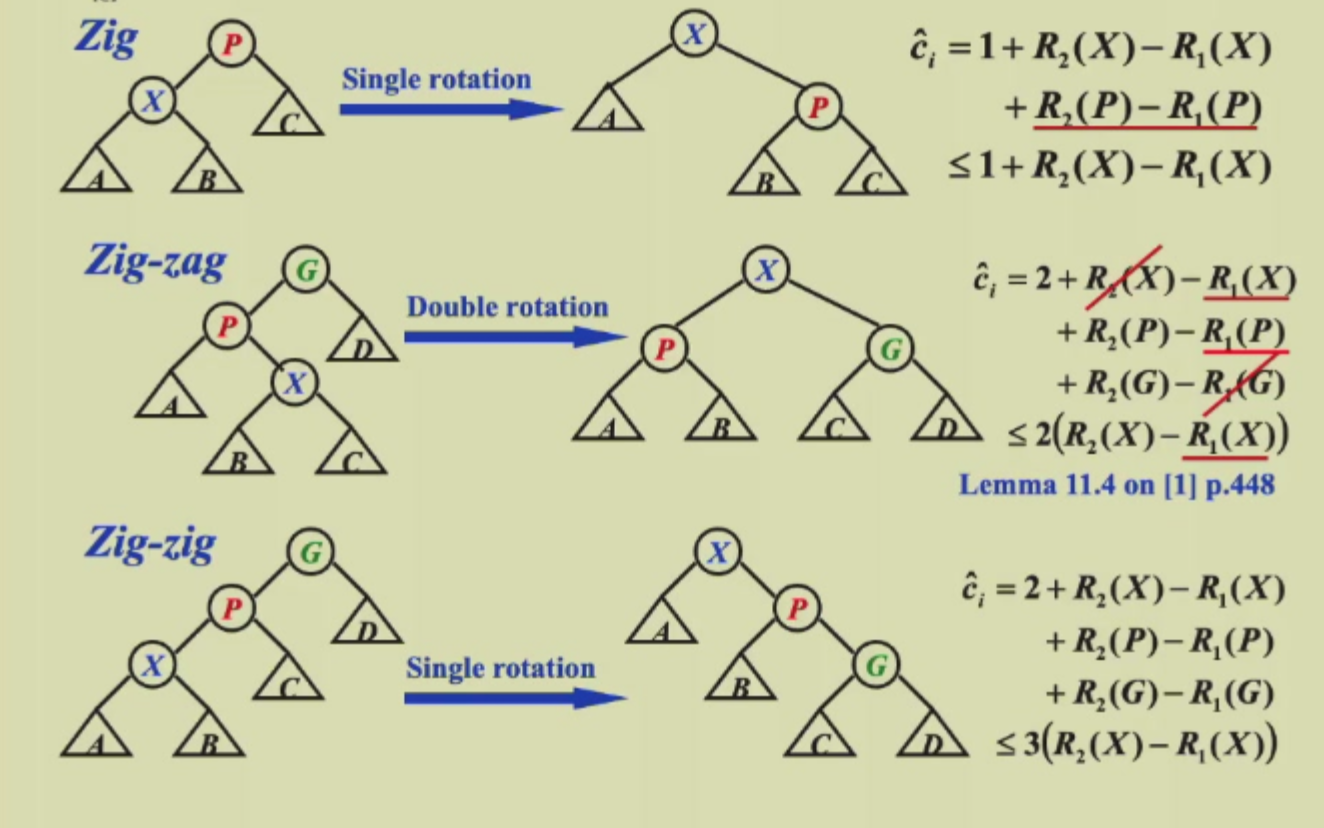
我手写了一下这三个放缩的过程：

ads-7

评论区

欢迎在下方留言~