Dynamic Programming¶
约 1676 个字 91 行代码 2 张图片 预计阅读时间 7 分钟
TODO:感觉ads课程中的dp讲的有点简单有点少,假期时准备多学一点
Intro¶
核心思想是避免重复计算,通过将计算结果存储在表格中,从而在需要时快速检索。
Fibonacci
计算Fibonacci数列:我们在递归时会对相同的数值进行重复计算,所以将每个n的Fibonacci数列的值存储在表格中
但是更好的方式是存下最近两次的计算结果,这样只需要\(O(n)\)的时间复杂度
Design¶
-
用状态函数表示一个子问题
-
状态转移方程表示子问题之间的递推关系
条件:
- 问题可以被分解为若干子问题
- 子问题有重叠
- 最优子结构:当前问题的最优解只依赖于子问题的最优解
Examples¶
Ordering Matrix Chain Multiplication¶
两个矩阵的乘法的基本复杂度是\(O(n^3)\)
但是对于一串连续的矩阵链乘法,对于不同的矩阵链顺序,其计算复杂度可以相差很大
Different Order
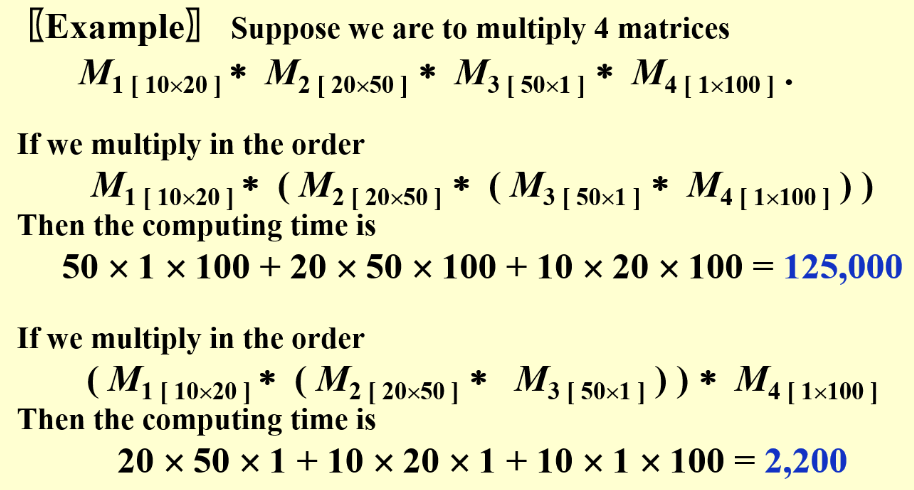
策略是优先计算规模较小的矩阵乘法。
Solution
用打括号的方式表示矩阵链的划分,如果括号是在第\(i\)个矩阵的右侧,我们就这样表示:
这也是动态规划和分治法的一个小技巧,就是直接想一下最后一步的计算,这里由\(M_{1,i}\)和\(M_{i+1,N}\)的计算结果相乘得到\(M_{1,N}\)就是这个问题的最后一步,我们就是去找最好的\(i\)
在这里我们规定状态方程为\(F[k][i]\),表示由第\(i\)个矩阵到第\(i+k\)个矩阵相乘的计算时间开销,k表示的是矩阵链的长度,这样在代码中我们先对k进行遍历(如果先对i,j遍历,是错误的,因为我们在计算前半部分时,后半部分根本还没有计算)这个遍历是严格按照子问题规模从小到大的顺序进行的
小技巧
我们在设计状态函数时,可以按照ppt中的i到j的思路,但是这样对代码设计来说不是很友好,yy哥建议我们在状态转移函数中,第一个参数k表示问题的规模,这样在代码中最外层的遍历就是对问题的规模进行放大的过程了
Brute Force
我们可以直接利用暴力方法,枚举所有可能的矩阵链划分,然后计算每种划分方式的计算时间开销,然后找出最小值,但是这个方法最后得到的总的计算次数是:
这也是一个状态转移方程,他表示的是计算n个矩阵所需次数,这个计算复杂度是\(O(\frac{4^n}{n^{3/2}})\)(Catalan Number),显然是不可接受的
我们在之前的思路中提到了,问题的最后一步就是合并两个矩阵链,在合并时,我们需要确定最后一个括号的位置,这需要我们进行遍历,因此我们可以得到状态方程:
其中\(r_i\)表示的是第\(i\)个矩阵的行数或列数
这个方程的意思就是,我们遍历所有可能的括号位置,然后计算每种划分方式的计算时间开销:括号左边矩阵链开销 + 括号右边矩阵链开销 + 合并两个矩阵链的开销
顺序实现code
int MatrixChainOrder(int p[], int n) {
// p[]存储矩阵维度,p[i-1]和p[i]表示第i个矩阵的维度
// n是矩阵的个数
int F[n][n]; // F[k][i]表示从第i个矩阵开始,长度为k的子链的最小计算代价
// 初始化:单个矩阵的计算代价为0
for(int i = 0; i < n; i++) {
F[0][i] = 0;
}
// 按照子问题规模k从小到大计算
for(int k = 1; k < n; k++) { // k表示子链长度
for(int i = 0; i < n-k; i++) { // i表示子链起始位置
F[k][i] = INT_MAX;
// 尝试在不同位置切分
for(int j = i; j < i+k; j++) {
// 计算在位置j切分的代价
int cost = F[j-i][i] + // 左半部分代价
F[k-(j-i+1)][j+1] + // 右半部分代价
p[i]*p[j+1]*p[i+k+1]; // 合并两部分的代价
if(cost < F[k][i]) {
F[k][i] = cost;
}
}
}
}
return F[n-1][0]; // 返回整个矩阵链的最小计算代价
}
记忆化搜索code
#define MAX_N 100
#define INF 0x3f3f3f3f
int memo[MAX_N][MAX_N]; // 记忆化数组
int p[MAX_N]; // 存储矩阵维度
// 计算从第i个矩阵开始,长度为k的子链的最小计算代价
int dp(int k, int i) {
// 基础情况:长度为0(单个矩阵)
if(k == 0) return 0;
// 如果已经计算过,直接返回记忆化的结果
if(memo[k][i] != -1) return memo[k][i];
// 初始化为最大值
int min_cost = INF;
// 尝试所有可能的切分点
for(int j = i; j < i+k; j++) {
int cost = dp(j-i, i) + // 左半部分
dp(k-(j-i+1), j+1) + // 右半部分
p[i] * p[j+1] * p[i+k+1]; // 合并代价
if(cost < min_cost) {
min_cost = cost;
}
}
// 存储并返回结果
return memo[k][i] = min_cost;
}
int MatrixChainOrder(int dimensions[], int n) {
// 复制维度数组
for(int i = 0; i < n; i++) {
p[i] = dimensions[i];
}
// 初始化记忆化数组为-1
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
memo[i][j] = -1;
}
}
// 计算整个矩阵链的最小代价
return dp(n-1, 0);
}
时间复杂度:\(O(n^3)=状态数 O(n^2) \times 状态转移的时间开销 O(n)\)
Optimal Binary Search Tree¶
最佳静态查找树
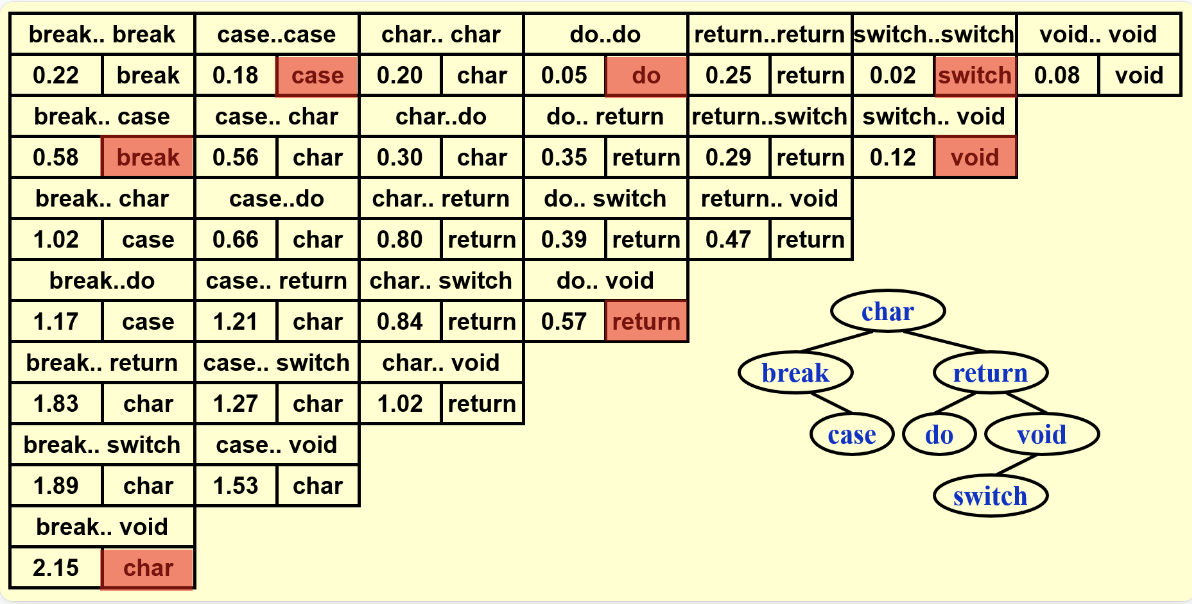
给出N个关键字\(w_1, w_2, ..., w_n\),以及每个关键字的查找概率\(p_1, p_2, ..., p_n\),要求构造一棵二叉查找树,使得所有关键字的总查找次数最小
查找次数公式:
Solution
还是按照之前的思路,在考虑最后一步时,我们考虑最后一步的根节点,然后计算左子树和右子树的查找次数,然后合并,并且由于合并时新增了一个根节点,整个树的深度都增加了1,因此要再加上\(p_{\text{all in this step}}\),并且这一步也是需要进行遍历的,因此我们得到状态方程:
Floyd Algorithm¶
Floyd
在一个有向图中,找到所有两点之间的最短路径
Solution
这个问题本质上是在解决对于有向图上任意两点之间,经过怎样的路径(经过几个中转点),使得路径上的权重和最小
我们从正常的思路先进行试探性的分析,先考虑构建一个普适性的状态方程:\(F[N][i]\)发现完全不适用,因为答案肯定是由i到j的,而与问题规模(图的大小)无关,因此我们考虑状态方程为\(F[i][j]\),表示从i到j的最短路径,根据之前的经验,我们可能需要一个最后的中转点K,写成\(F[i][j] = \min \{ F[i][k] + F[k][j] \}\)这样的方程
但是错误
因为在这个问题中,我们所求解的不再是像之前的矩阵链乘法那样的带有序列性质的问题,而是任意两点之间的最短路径,这个路径可以经过很多节点(问题规模未被定义),因此这个方程无法保证子问题按照从小到大的顺序进行求解
所以我们需要对函数进行限制,限制参数就是经过的中转点的个数,这样我们就可以按照中转点个数从小到大进行求解,得到状态方程:
其中\(F[k][i][j]\)表示的是从i到j,经过k个中转点的最短路径,\(F[k-1][i][j]\)表示的是从i到j,不经过第k个中转点的最短路径,\(F[k-1][i][k] + F[k-1][k][j]\)表示的是从i到k,再从k到j,经过第k个中转点的最短路径
留言