ADS¶
AVL Tree¶
Intro¶
在数据集中快速查找、插入、删除、排序等操作时具有较好的效果
Target:Speed up
基本思想:
height balance:每个节点的左右子树的高度差(平衡因子BF)不超过1
PS:树的高度计算:由根节点到叶节点的最长路径 -> 进行高度平衡
Operation¶
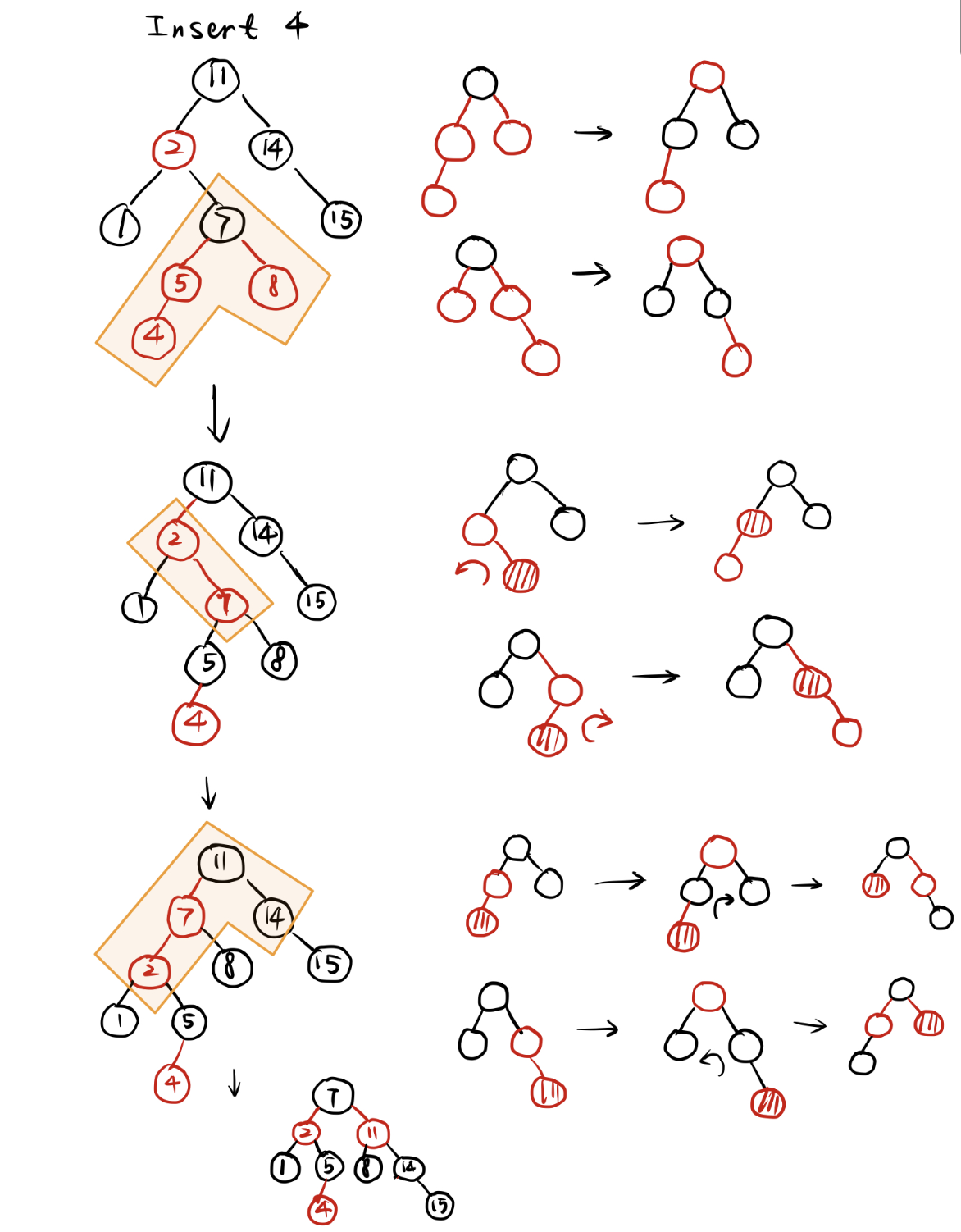
Rotation 在不改变树的相对顺序的情况下,通过旋转操作来调整树的结构,使得树的高度平衡

想象将需要被提高的节点提高,将需要被降低的节点降低,然后将这两个节点的子树连接到新的节点上
Time Complexity: \(O(1)\)
因为只有四个节点更新
B、A、y、A的老子
- RR Rotation or LL Rotation 右子树的右节点插入导致右子树的父节点BF=2,将BF=2的右子节点提高,B连接的左子树连接到A的右子树上
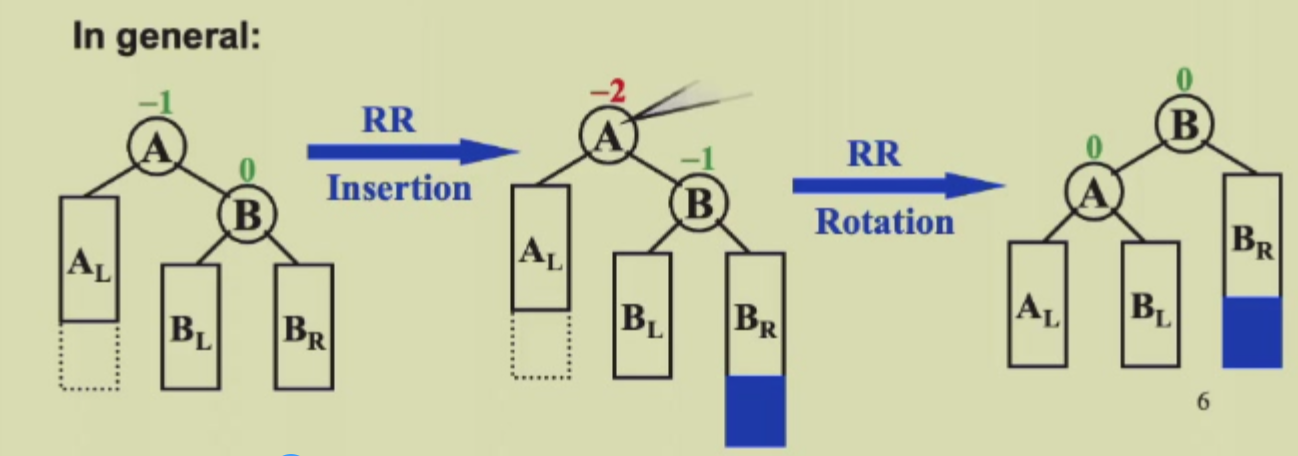
若遇到多个节点BF非法的情况,只需要对最底部的两个节点进行旋转操作即可
- LR Rotation or RL Rotation 左子树的右子节点增加导致左子树的父节点BF=2,将左子树的右节点提高两次
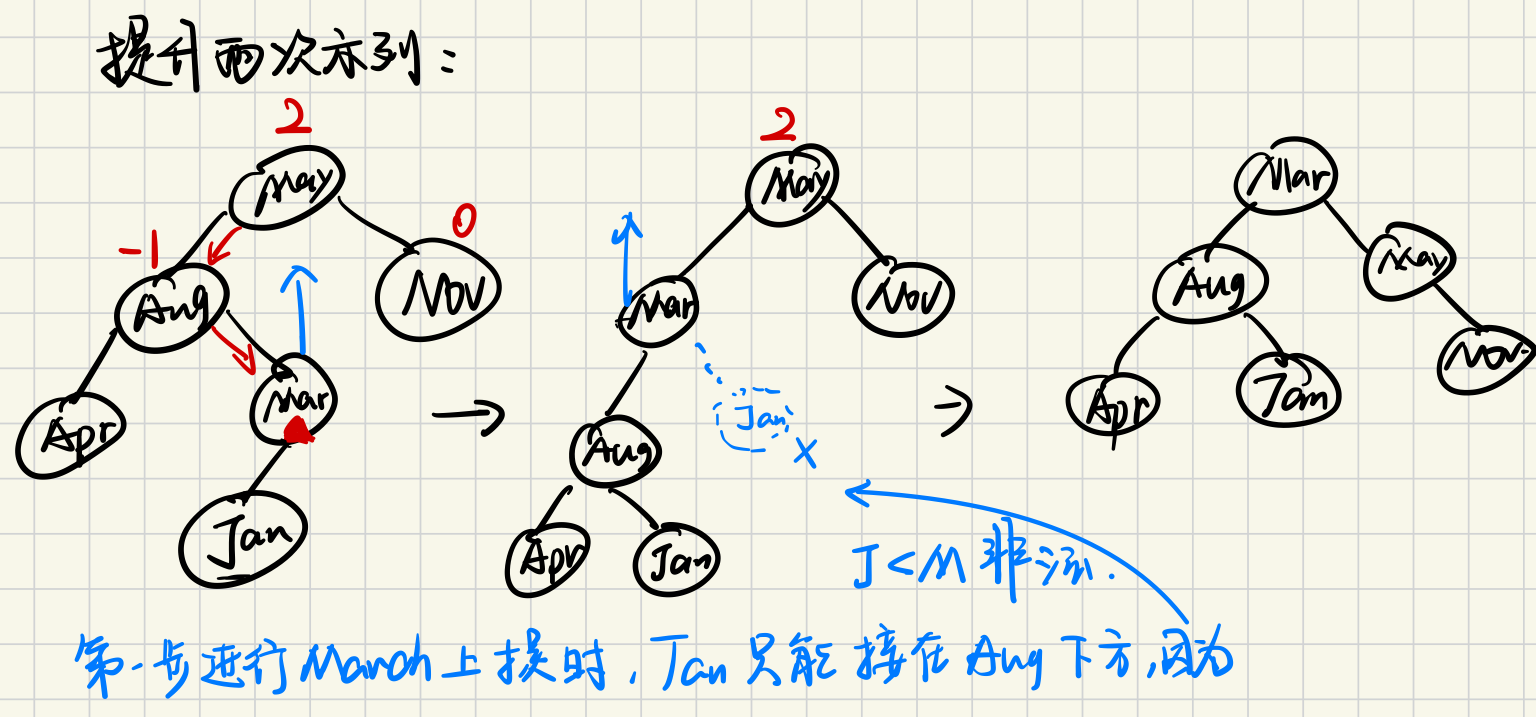
按照片上的解释根据树的合法性可以推出中间步骤 也可以这样理解: 在对Mar进行旋转时,Mar的左位是被占用的,而Mar的父亲是比Mar小的,只有把Jan移开才能给Aug腾出位置
- 最小节点数:
\(n_h\):高度为h的最小节点数 为了保持树有h的高度,至少一个子树的高度为h-1,另一个子树的高度与他相差为1,= n-2 因此:
可以得到:
Splay Tree¶
Intro¶
Target: 由空树进行M个连续操作最多需要\(O(M \log N)\)的时间
即:Amortized Time Complexity 均摊时间复杂度 = \(O(log N)\)
Operation¶
将最近访问的节点提升到根节点,这一操作通过旋转来实现
Splay Tree vs AVL Tree
要注意不要将splay tree和AVL树的操作进行参照,splay tree的操作对象是一直固定的,而AVL树的操作对象是根据平衡因子决定的
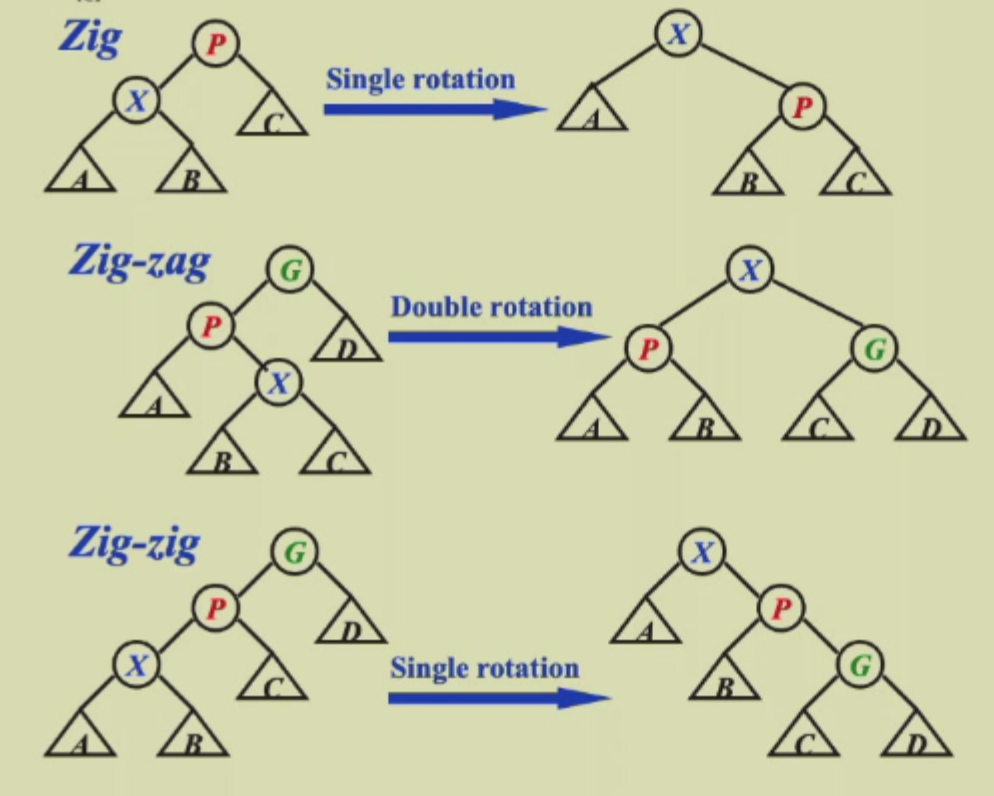
- Zig Single Rotation
没有G,只转一次X
- Zig-zag
Double Rotation 转两次X
像AVL树的LR和RL
- Zig-zig
Single Rotation 先转X再转P
Operation
- 将新节点插入到树中
- 将新节点旋转到根节点
- 将待删除节点旋转到根节点
- 将根节点删除得到两个子树T1和T2
- FindMax(T1)或者FindMin(T2)作为新的根节点
Red-Black Tree¶
Intro¶
AVL树是通过实现高度平衡来进行优化 而红黑树是通过实现颜色平衡来进行优化
NIL节点
在树的代码中,遇到了叶子结点时需要if判定空,常用一个哨兵节点来避免大量的if语句,但是为了避免空间的浪费,在红黑树中,我们使用了一个NIL节点来代替哨兵节点,所有的叶子节点和根节点都指向(同一个)NIL节点
红黑树的性质:
- 每个节点要么是红色,要么是黑色
- 根节点是黑色
- 每个叶节点(即NIL节点)是黑色
- 如果一个节点是红色,那么它的两个子节点都是黑色
- 对于每个节点,从该节点到其所有后代叶节点的路径上,均包含相同数目的黑色节点
black height:从某节点(不包含自身)到叶节点的黑色节点的个数
Lemma
一个有N个内部节点的红黑树的树高至多为\(2\log_2(N+1)\)
Black Height
证明:设空树的树高为0
归纳假设:
归纳奠基显然在空树上成立
归纳演绎:
对一个非空树时:\(h(x) \leq k\) 成立,现在证明\(h(x) \leq k+1\)也成立
对一个x满足\(h(x) \leq k+1\),其子树的黑高要么等于x的黑高,要么等于x的黑高-1(子树的根节点是红色)
因为:
则有: $$ sizeof(child) \geq 2^{bh(child)}-1 \geq 2^{bh(x)-1}-1 $$ 即子树的节点数有一个下界
由于: $$ bh(Tree) \geq \frac{h(Tree)}{2} $$ 则: $$ Sizeof(Tree)=N \geq 2^{bh(Tree)}-1 \geq 2^{h/2}-1 $$ 得证
Operation¶
前提
在这里我们假设在插入前树是满足红黑树性质的,因此进行对比的是插入红色节点前后的性质情况,只需要考虑操作前后是否相对平衡 补药计算例子中的绝对黑高
- Insertion 两个性质需要保持:
- Key值保证二叉树
- 红黑树性质
默认插入的节点为红色,插入后不会破坏第五条性质,但是继续插入后可能会遇到连续的红色节点,这时需要进行补救
需注意性质2可能因为插入的是空树被破坏,这时需要将根节点涂黑
接下来的分类讨论其实就是根据叔叔的颜色进行旋转,
Case 1
具有对称情况:LL(图中)、LR、RL、RR
叔叔节点是红色
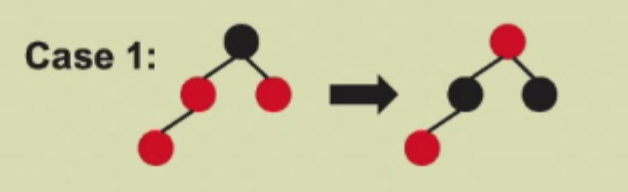
插入一个节点后,父亲与叔叔都是红色,这时将父亲涂黑,发现左树的黑高比右树的黑高多1,再将叔叔涂黑,发现整棵树对于树外部分整体黑高+1,这时将祖父涂红,满足了红黑树的性质,但是会遇到祖父的父亲是红色的情况,这时需要递归处理
这也是插入唯一需要迭代的操作
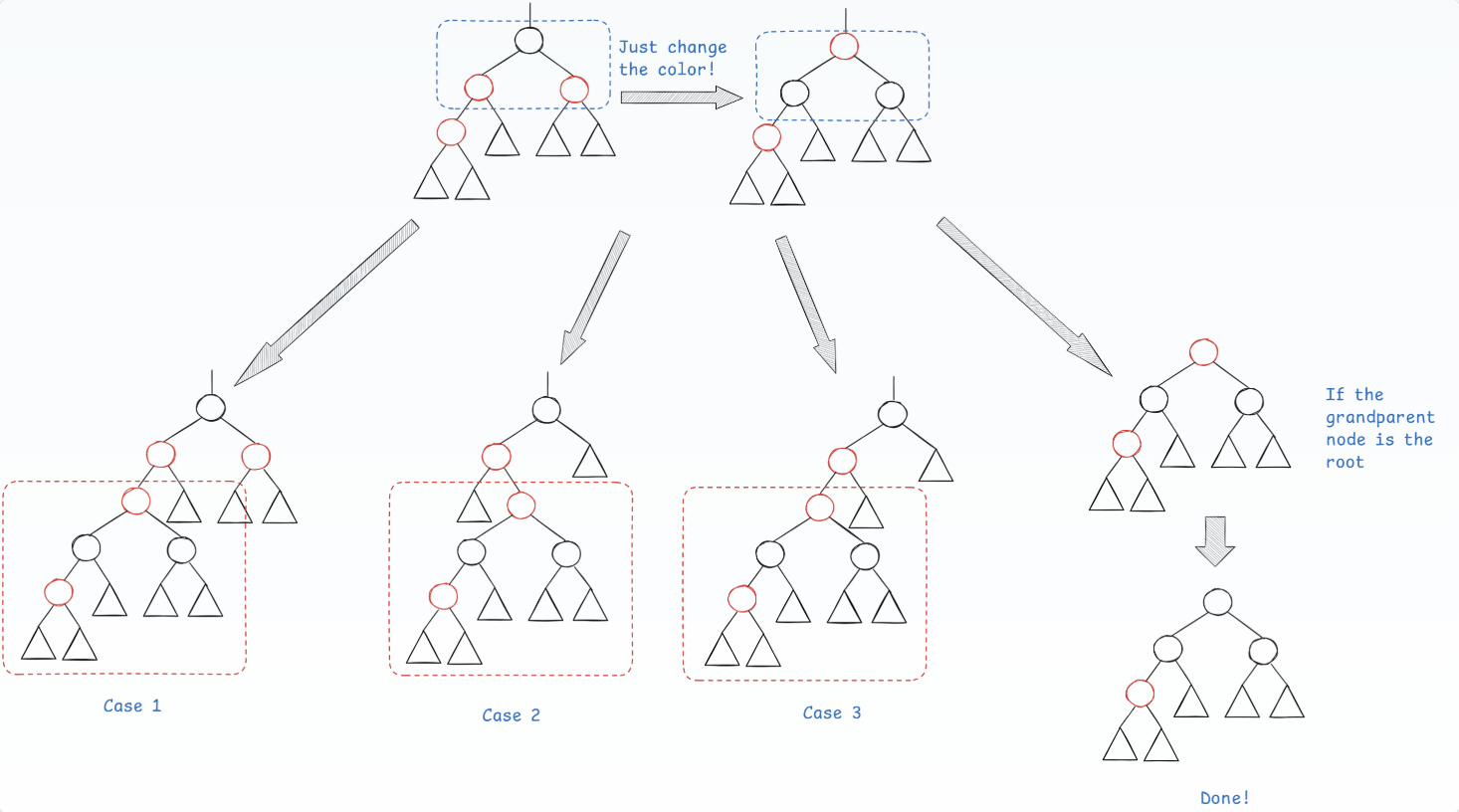
可以看到我们在进行case1的操作后可能进入到任何一种情况
Case 2
具有对称情况RL
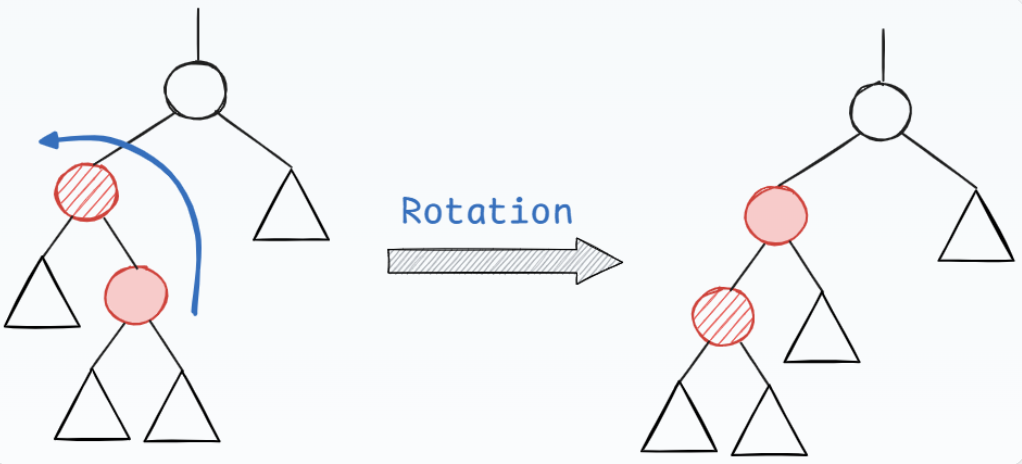
叔叔的颜色是黑色,且插入节点靠近叔叔节点,此时无法通过传递祖父的黑色维持黑高,需要进行旋转操作,将插入节点与父亲进行旋转,进入Case 3
Case 3
具有对称情况RR
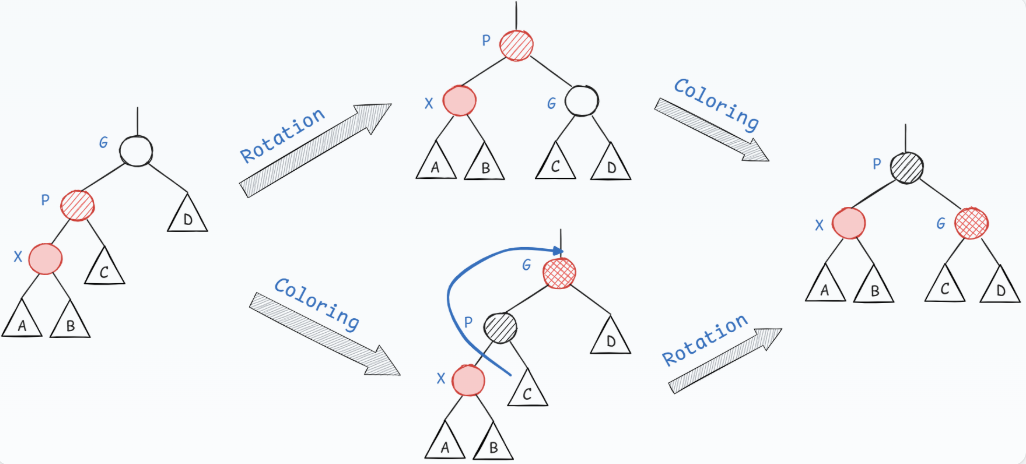
先将爸爸染黑,爷爷染红,此时左子树的黑高比右子树的黑高多1,因此要进行右旋转平衡黑高
最后对insertion进行总结:(来源于noughq同学的笔记)
- Delete
我认为自己写的红黑树删除是一坨屎,但是考试周来不及更新别的好方法了,期末周结束我会更新一下的()如果忘了()不是 应该不会忘。。。太屎了。。。。。。。。。。。。。。。
总体的思路是将删除节点增黑,然后通过转移这个黑色到父亲节点,在进行黑高的平衡,当然最简单的情况就是删除节点是红色,这时直接删除即可,其次删除节点删除节点只有一个孩子(只能是红孩子)代替他爹后变黑即可
然后我们讨论删除节点是黑叶子的情况,这里需要引入一个双黑的概念,即删除叶节点是黑色,那么在删除它之后将它的黑色增加到2,再通过旋转和染色操作平衡黑高,最后将其变为单黑NIL
Case 1

删除节点是黑色,父亲也是黑色但是兄弟是红色,此时将兄弟染黑,父亲染红,但是这样会使黑高右移,因此需要进行左旋转,旋转之后进入到Case 2
Case 2
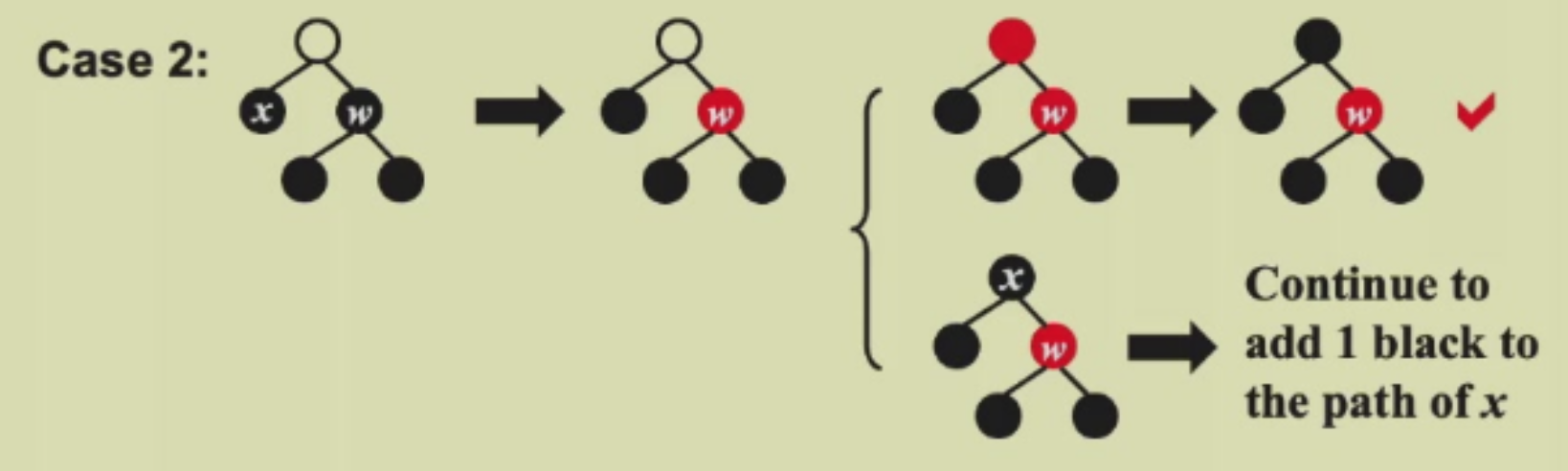
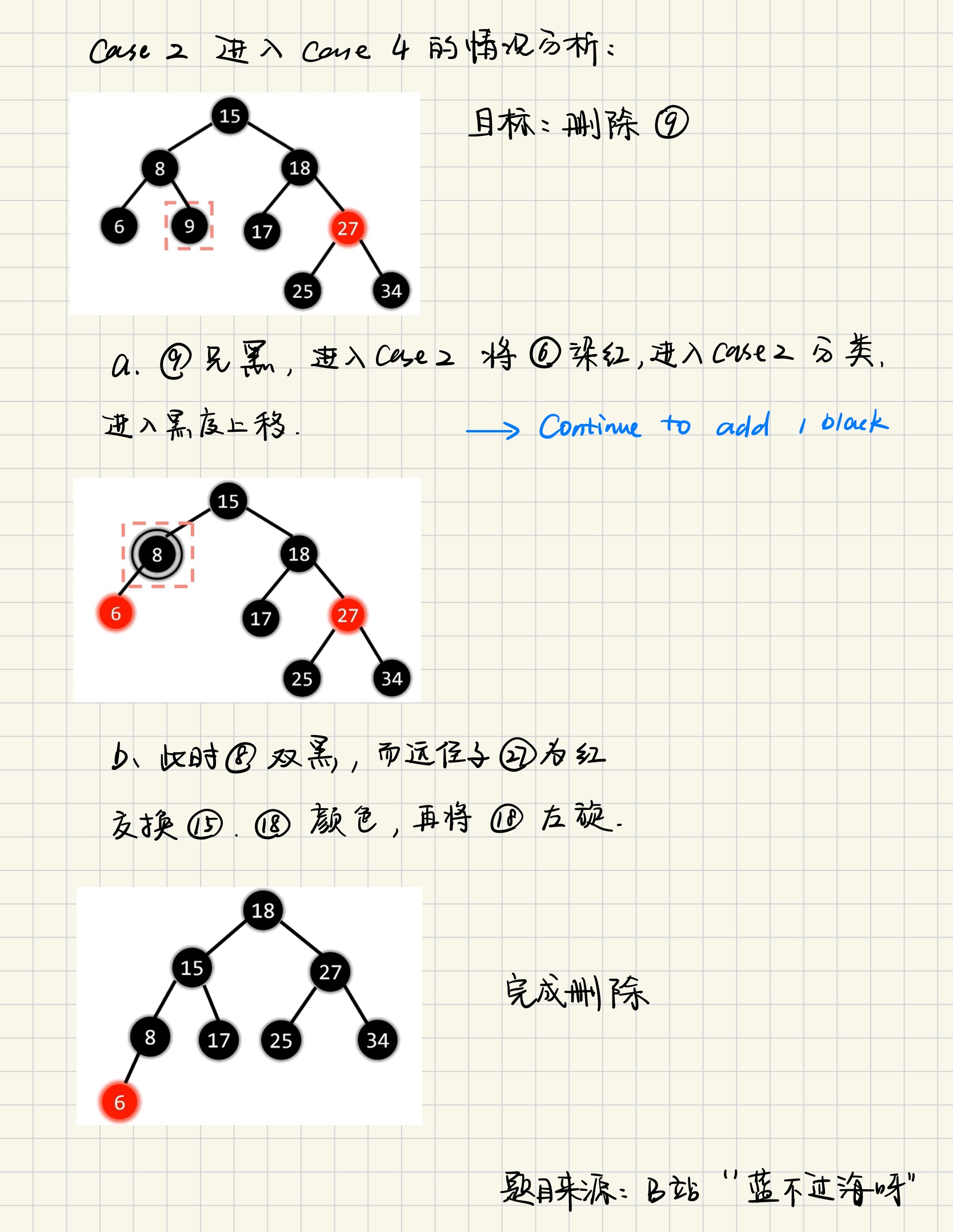
此时兄弟节点的颜色是黑色且侄子是双黑,这时候甩锅给父亲,将父亲染黑,此时右路黑色多了一个,然后在分类讨论,父节点本来是红色就结束了,染黑即可;父节点本来是黑色,就继续递归
此时需要注意的是一种情况就是所删除的节点一直递归到根节点时,一路上都没有红色节点,就会进入到Case 4,这时候需要进行旋转操作
我画出了这个操作的过程:
这时候问题出现了,如果侄子有红色,那么在Case 2中我们将兄弟染红的操作就是错误的,因为这样会导致两个连续红色,这就进入了Case 3
Case 3
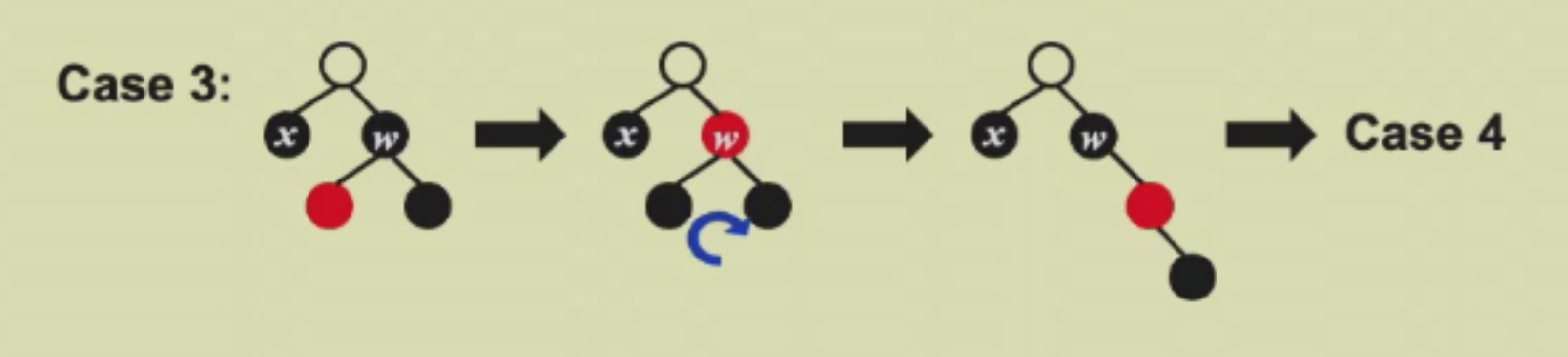
远侄子是黑色,近侄子是红色,此时将红色侄子与其黑色父亲互换,会导致左侄子这条路的黑高多1,因此需要进行右旋转,然后这时远侄子就是红色了,进入Case 4
Case 4
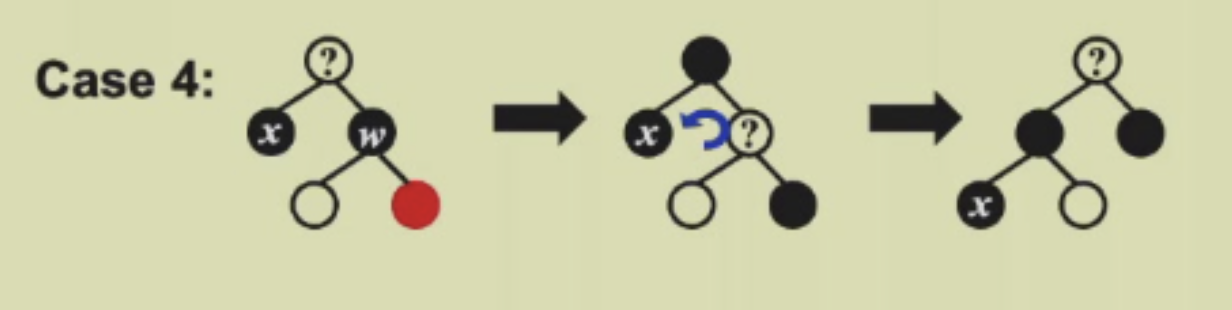
这个情况是:X是待删除节点,他的身上有两个黑色标记,他的兄弟是黑的,远侄子一定是红的,父亲和近侄子可红可黑,这时候的操作步骤:
- 将父亲和兄弟的颜色互换,为了避免父亲是红色导致右侧出现连续的红色,将侄子染黑
- 这时候的黑高右边有可能不变,也可能增大1向右边倾斜,进行一次左旋转
- 这时候待删除节点就位于叶节点上了并且黑高也平衡了,将其删除即可
如果从逆向的角度思考,具备直接删除一个黑色节点的条件,就是这个节点是叶节点并且他所在的路径上黑高多了一,这就是一直往左边塞黑色的原因,就是要让他成为一个可以直接删除的节点
总结:
- 先看兄弟是不是黑
- 再看侄子有没有红
- 侄子有红看远侄子
- 转化到远侄子为红
- 远侄为红一顿操作
Number of Rotations:
| AVL | Red-Black | |
|---|---|---|
| Insertion | \(\leq 2\) | \(\leq 2\) |
| Deletion | \(O(log n)\) | \(\leq 3\) |
B+ Tree¶
Intro¶
B树是一种平衡的树状数据结构,主要用于在磁盘上存储数据,减少磁盘的I/O次数
B-Tree with order B:
- 结构性质
- 根节点要么是叶子节点,要么有2到B个孩子
- 每个非叶子节点有\(\lceil \frac{B}{2} \rceil\)到\(B\)个孩子
- 所有叶子节点在同一层
- 数值性质
- 数值全部存放在叶子结点
- 非叶子结点中存储routing element,用于确定子树中数值的分布,\(\lceil \frac{B}{2} \rceil\)到\(B\)个孩子,称为他的fanout
- 非叶子节点中的元素个数+1=孩子个数
- 叶子节点存的元素个数在\(\lceil \frac{B}{2} \rceil\)到\(B\)之间,根节点作为叶子时可以存储1到B个元素
- 一个存储了\(K\)个元素\(e_1,e_2,e_3,e_4,e_K\)的internal node 有\(v_1,v_2,v_3,v_4,v_K\)这些叶子结点:
补充的性质:N表示元素个数
- leaves \(\leq \frac{N}{ \lceil \frac{B}{2} \rceil}\)
- nodes \(\leq \frac{2N}{ \lceil \frac{B}{2} \rceil}\)
- elements \(\leq 2N\) 这里用nodes数乘B得到的似乎是4N,但需要注意的是路径上的节点存储的数值全部是元素的副本,总数不会超过2N
这意味着B树的高度是非常低的(相较于二叉树的\(O(\log_2 N)\)),因此可以减少磁盘的I/O次数
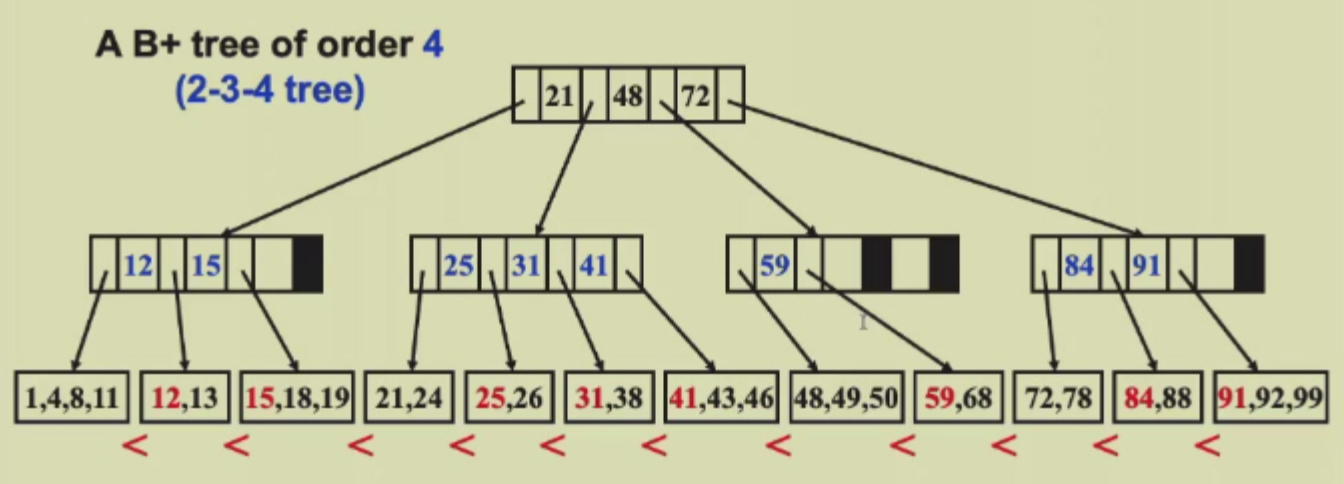
Operation¶
- FindKey
对routing element进行二分查找,找到对应的叶子节点,然后对叶子节点进行二分查找
这样得到的CPU时间复杂度为\(O(logN)\),也就是说,增加B树的阶数不会改变查找时间
磁盘的I/O次数为\(O(\log_B N)\)
- InsertKey
对于没有满的节点,直接插入即可,如果满了,则需要进行分裂操作,将节点分裂为两个节点,并将中间的元素更新到父节点,如果父节点也满了,则需要进行递归操作,直到根节点
有一个小的优化措施是在自己满员兄弟未满的时候,将元素移动到兄弟节点,这样可以减少分裂的次数,实现时需要定位到兄弟节点,因此添加一个指针指向兄弟节点,但是这个操作只会停留在共享一个父节点的节点之间,而避免遍历所有节点
CPU时间复杂度为\(O(B\log_B N)\),磁盘的I/O次数为\(O(\log_B N)\)
- DeleteKey
删除操作与插入类似,当所在的叶子节点在删除当前元素后元素个数小于\(\lceil \frac{B}{2} \rceil\),则需要进行合并操作,左右节点有\(\geq \lceil \frac{B}{2} \rceil+1\),时,可以直接借一个元素过来,否则需要将当前节点与左兄弟或右兄弟合并
时间复杂度与插入相同
Leftist Tree¶
Intro¶
满足最小堆的传统性质,即父节点的值小于等于子节点的值
同时满足左式堆的性质:
定义
任意一个节点x到一个 没有两个孩子的节点 的距离称为节点的null path length,记作\(npl(x)\)
显然,对于一个有左孩子和右孩子的节点,\(npl(x)=1+\min(npl(lc),npl(rc))\),对于叶子节点,\(npl(x)=0\),在这里我们定义\(npl(null)=-1\)
- 在左式堆中,\(npl(lc(x)) \geq npl(rc(x))\),即左孩子的null path length总是大于等于右孩子的null path length,因此,左式堆也被称为左偏树
一个没有两个孩子的节点
这里注意这个定义,如果一个节点只有一个孩子,那么无论他的这个孩子有多长,他的null path length都是0,因为我们定义了空节点的null path length为-1,而计算时:
对于一个有n节点的二叉树,若满足左式堆的性质,则有\(npl(root) \leq \log_2(n+1)\),即对于一个长度为r的right path,至少有\(2^r-1\)个节点
Operation¶
- Merge(H1, H2)

Merge Example
- DeleteMin(pointer to u)

Skewed Heap¶
Intro¶
很简单,不需要额外空间维护null path length,只需要在每次合并(递归返回)的时候对根节点的两个孩子进行一次旋转即可
可以看作是self-adjusting leftist heap
Operation¶
- Merge(H1, H2)
在操作时不进行npl的比较,直接左右互换,其余操作与左式堆相同
不支持删除和decrease key操作
Skewed Heap Merge Example
Inverted File Index¶
实现搜索引擎的方法:
没怎么听。。。
Binomial Queue¶
Heap-Ordered Tree: 满足堆性质的完全二叉树,包括Min-Heap Max-Heap
Priority Queue:不按照队列先进先出的顺序,而是按照某种优先级进出
二项队列不是单独的一棵树,而是一个森林
森林中的每一个树被称为二项树 binomial tree 并定义树的高度,高度为0的树是由一个节点构成
高度为k的树是由两个高度为k-1的树合并而成,在这里合并时,根节点最小的树作为新的根节点,同时将另一个树作为新的根节点的孩子,也就是说另外一棵树是直接连接到根节点上的
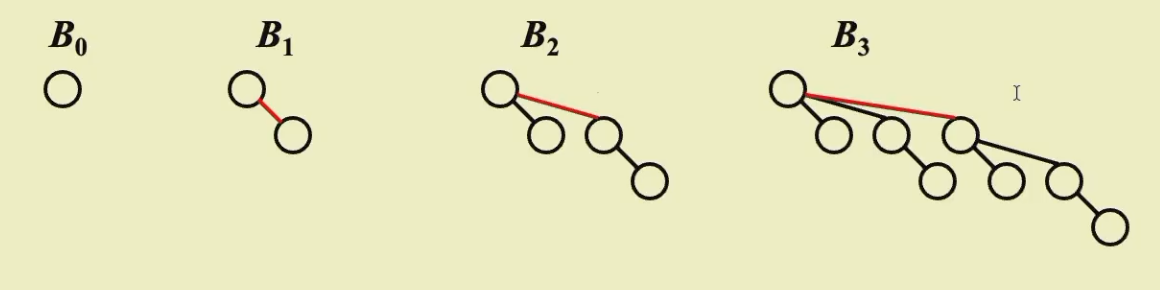
\(B_k\)表示高度为k的二项树,\(B_k\)有\(2^k\)个节点,根节点的度数为k,根的孩子从左到右依次为\(B_{k-1},B_{k-2},...B_0\),在d深度层有\(\binom{k}{d}\)个节点
性质: BQ 中每个高度的树至多有一棵,也就是说,每一个BQ都可以被唯一的表示为一个二进制分解
Operation¶
- FindMin
每个二项树的根节点都是最小值,因此只需要遍历每个二项树的根节点即可找到最小值,而一个n个节点的BQ中,最多有\(\lceil \log_2 n \rceil + 1\)棵树,因此时间复杂度为\(O(\log n)\)
但是,如果需要频繁的进行FindMin操作,则需要维护一个最小值的指针,这样可以将时间复杂度降低到\(O(1)\)
- Merge
思路就是二进制加法,从最低位开始,单独存在的二项树保留,同时存在的二项树合并成为层数+1的新的二项树
每次合并的时间复杂度是\(O(\log 1)\),总共的时间复杂度为\(O(\log n)\)
- DeleteMin
找到最小的元素所在的二项树\(O(\log n)\),将这个树单独拿出来\(O(\log n)\),去除根节点\(O(\log n)\),得到一个新的BQ,这个新的BQ与之前剩下的树进行合并,时间复杂度为\(O(\log n)\)
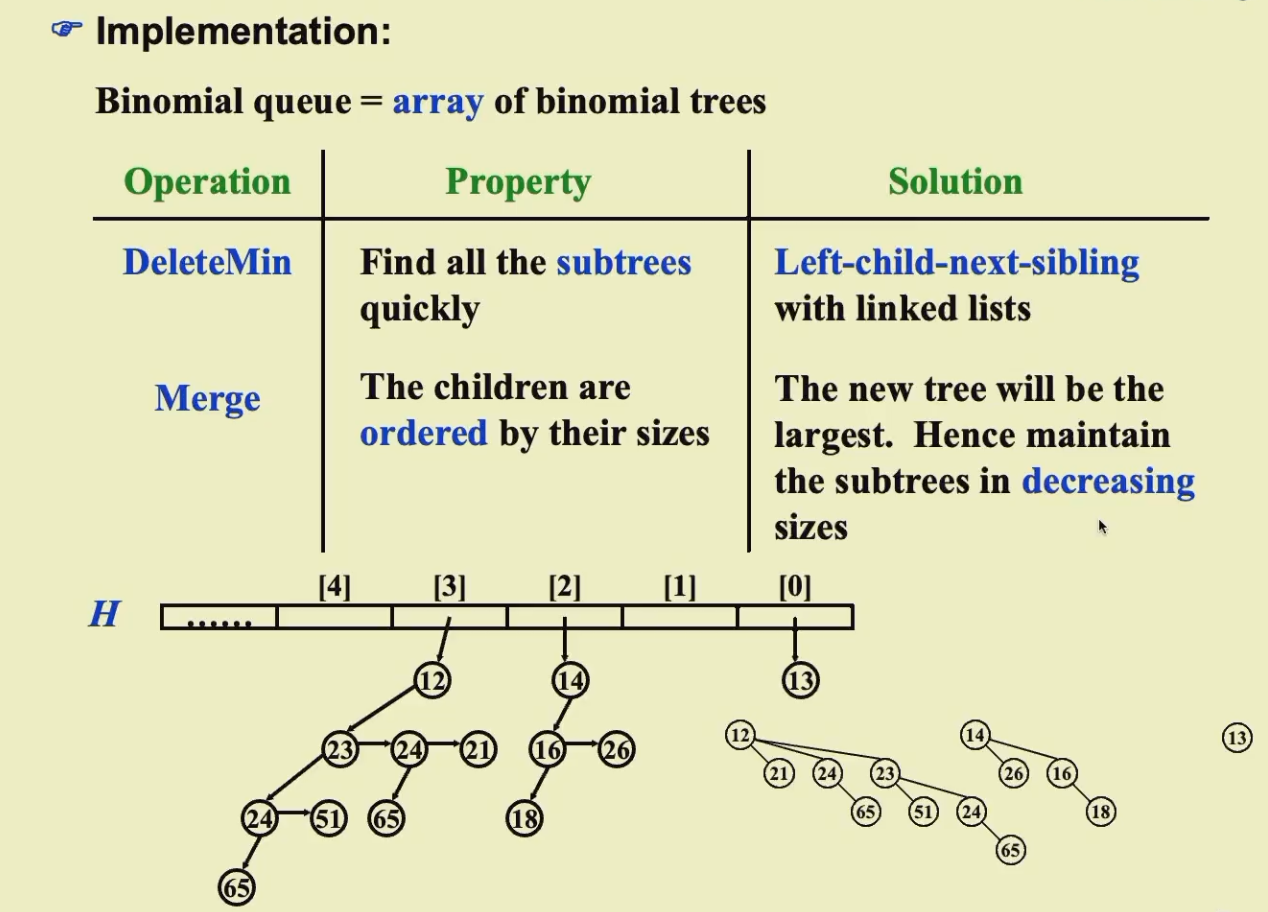
可以看到二项队列中每一个二项树的实现是通过左孩子右兄弟的表示方法实现的
连续的插入操作:均摊时间复杂度是\(O(n)\)
Proof


2-c的推导:
因为每c次操作,可以被分解为1次的step和c-1次的合并,而合并增加的树的个数是-1,所以得到2-c
留言