Arithmetic¶
Numbers¶
- Two's Complement
正数最高位为0,负数最高位为1。
正数正常表示,负数取反加1。
Add & Sub¶
Multiplication¶
乘法器的实现就是加法器,但是需要进行移位和多次加法。
Version 1
实现一个64位的乘法器,需要128位的加法器:
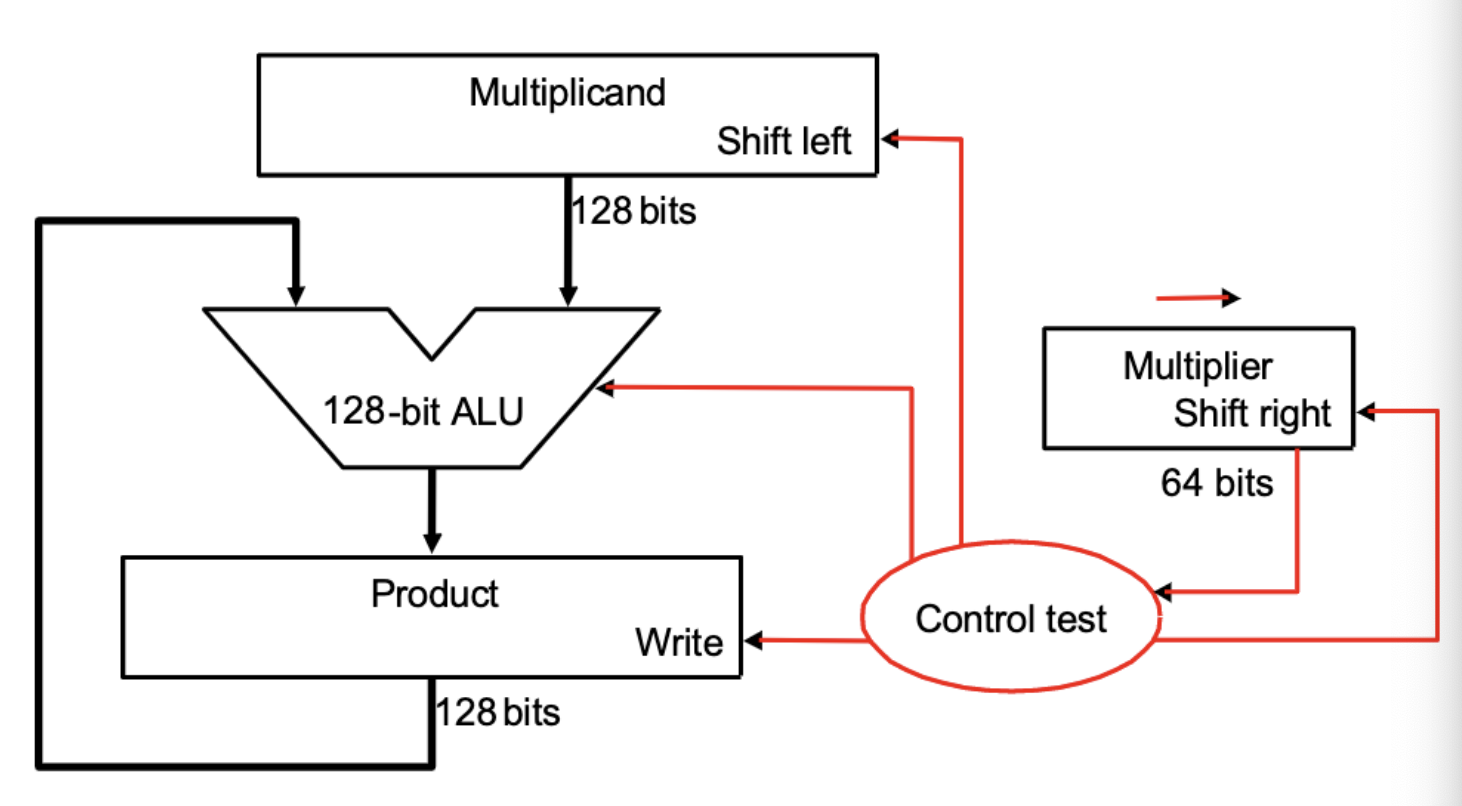
还是比较好理解的,就是模仿手写乘法的过程:非常的复杂缓慢,运用128位加法器,但是真正在相加的只有64位。
在乘数(Multiplier)的当前位为1时,将被乘数(Multiplicand)加到乘积(Product)上,然后乘数右移,被乘数左移。(这里乘数右移是因为我们每次只看乘数的最低位是否为1,在看完了之后需要看下一位,所以需要右移)
在乘数(Multiplier)的当前位为0时,乘数右移,被乘数左移。
进行64次循环后结束。
Version 2
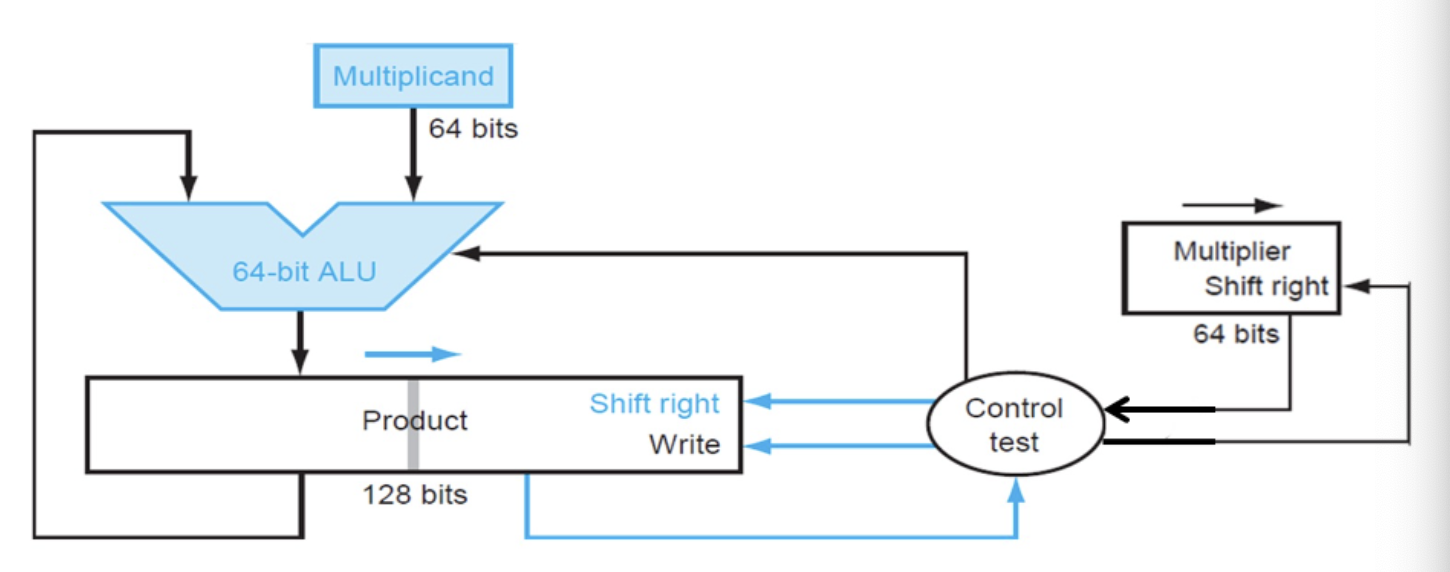
改变思路,移动乘积,这样避免了使用较大的加法器。
这里需要一个128位的寄存器作为乘积寄存器,分为高64位和低64位,刚开始第一个乘积放在最高位。
在每次循环中,如果乘数最低位为1,将被乘数加到乘积寄存器的的高64位,然后乘积寄存器右移,乘数右移;
如果乘数最低位为0,乘积寄存器右移,乘数右移。
经过64次循环后,乘积寄存器的低64位就是我们想要的结果了。
Version 3
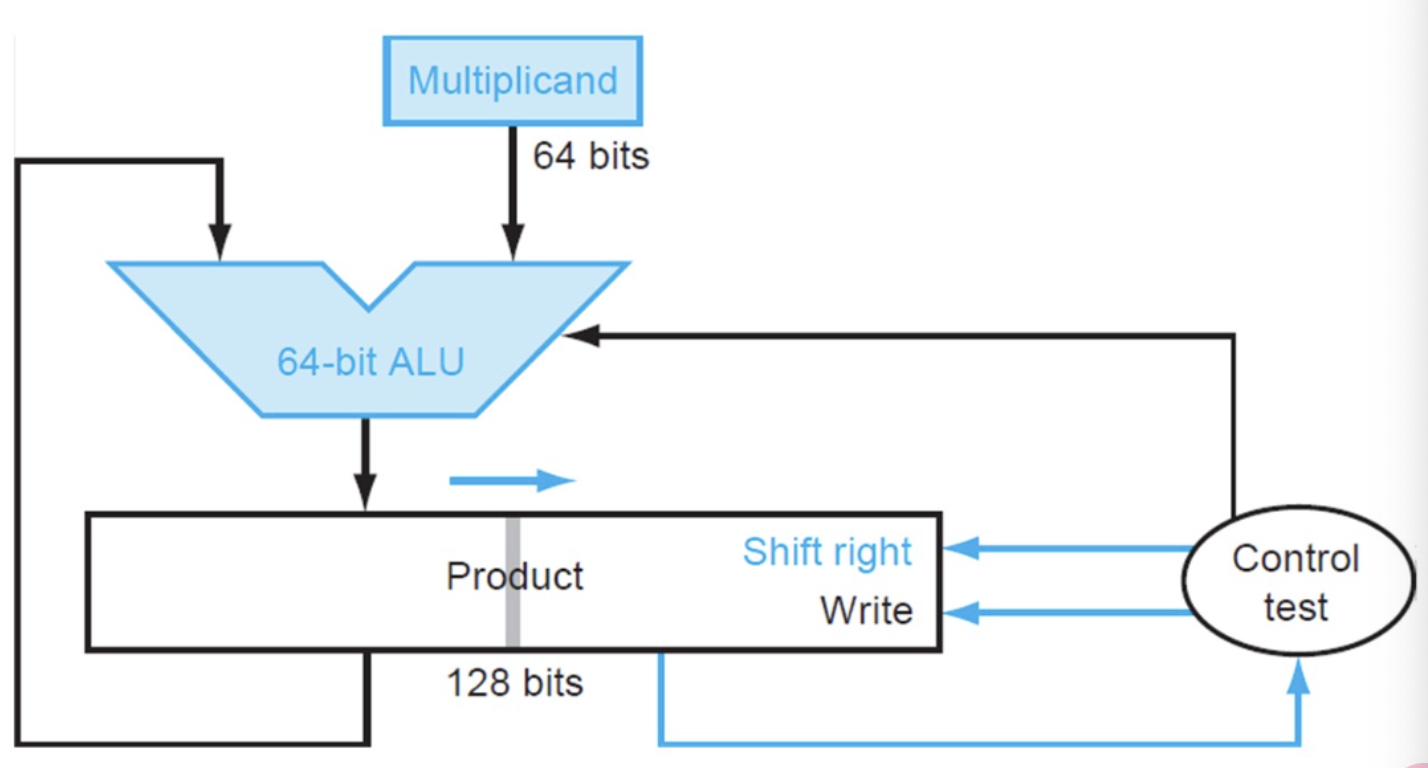
在先前的版本中,乘积寄存器最终会有一半的空间是浪费掉的,这一半的长度正好与乘数的长度相同,因此我们可以用128位乘积寄存器初始的右半部分来存储乘数,这样就不需要乘数寄存器了。
Example
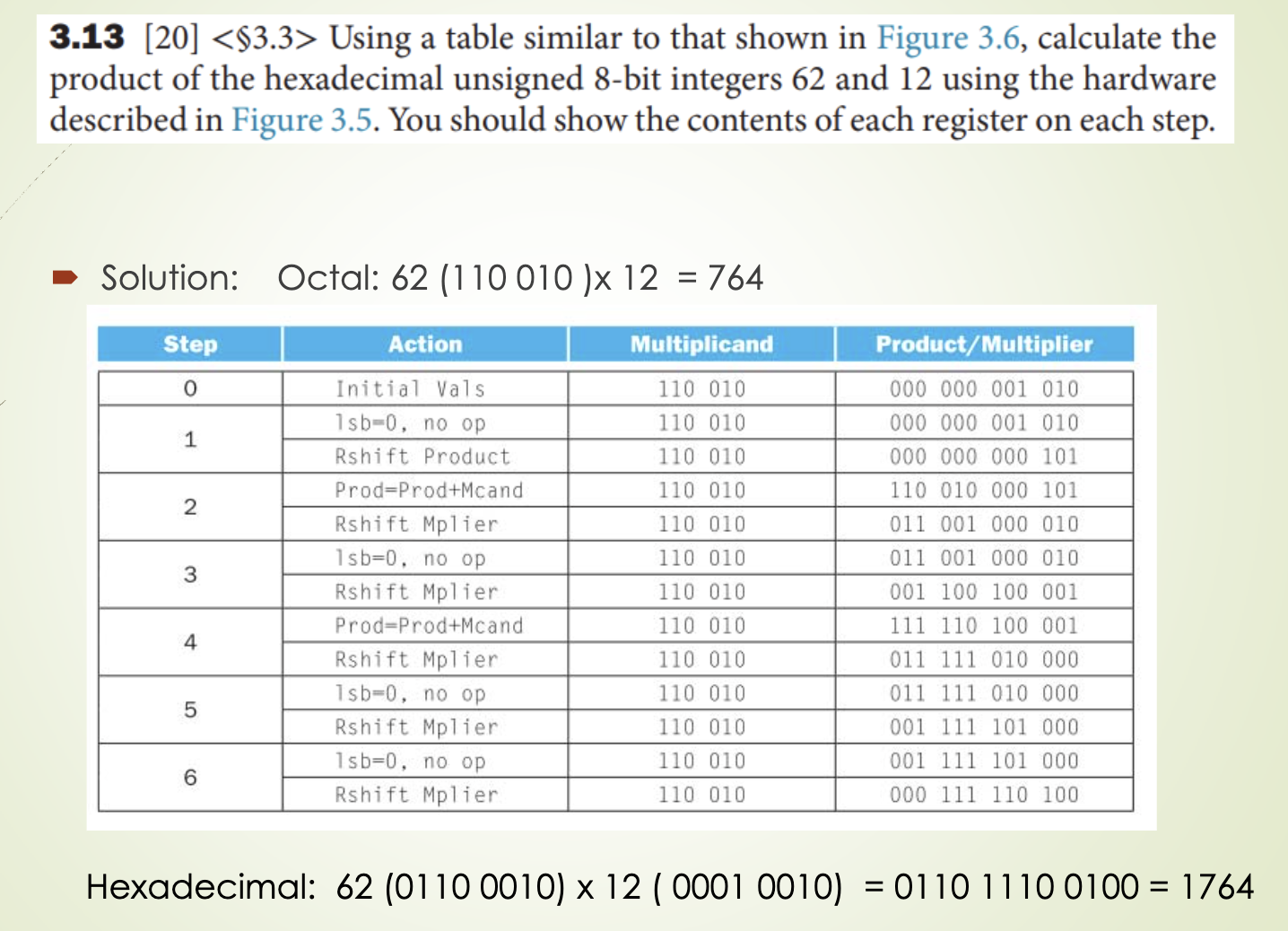
这个例子就是Version 3的实现过程,需要注意的是我们运用这个算法可以适配不同的数据格式和长度,比如这个书写过程中就是用6-bit的八进制数进行运算,同时下方还给出了同样数据如果是8-bit的十六进制数进行运算的结果。
对有符号数乘法,需要存储符号位,然后进行无符号数乘法,最后根据符号位确定结果的符号。
但是注意
Warning
乘法不能用补码计算
- Improved Multiplier
Booth's Algorithm
我不想写了,放了xyx学长的笔记: 🔗
Division¶
Version 1 除法最初的版本也是模仿手写除法:
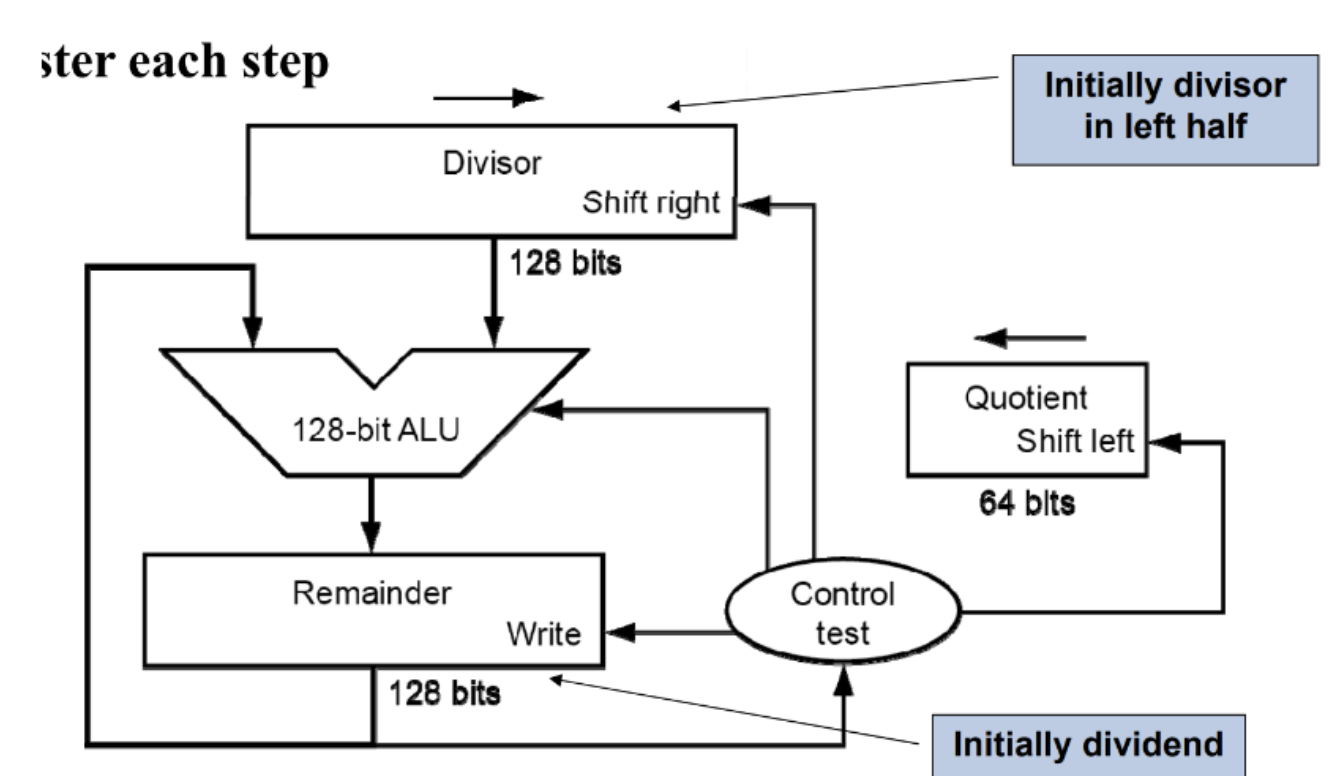
进行除法时,主要是通过判断余数的正负来进行的
除数初始时存放在除数寄存器的高位半边,余数寄存器初始时是存放被除数并放在低位半边的,
从余数寄存器中减去除数,如果结果为正,左移商寄存器,将最新的右位设为1,如果结果为负,将除数寄存器加回到余数寄存器,左移商寄存器,将最新的右位设为0。
这之后将除数寄存器右移一位,重复65次循环后结束。
Version 2
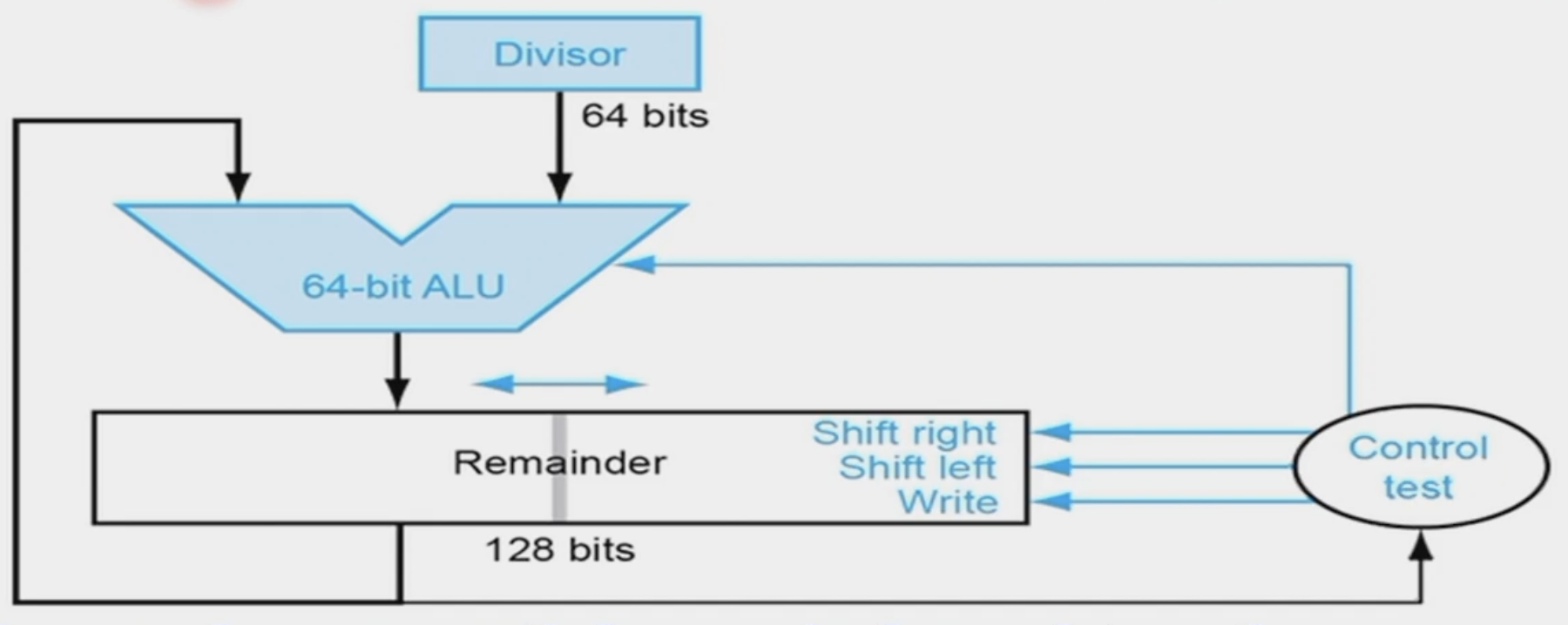
除数不动,被除数放在128位余数的低位半边
循环开始时,先将余数部分左移一位,然后减去除数,如果结果为正,左移余数寄存器,将最新的右位设为1,如果结果为负,将除数寄存器加回到余数寄存器,左移余数寄存器,将最新的右位设为0。
这样最后余数寄存器低半位就是商,高半位就是余数。
7/2
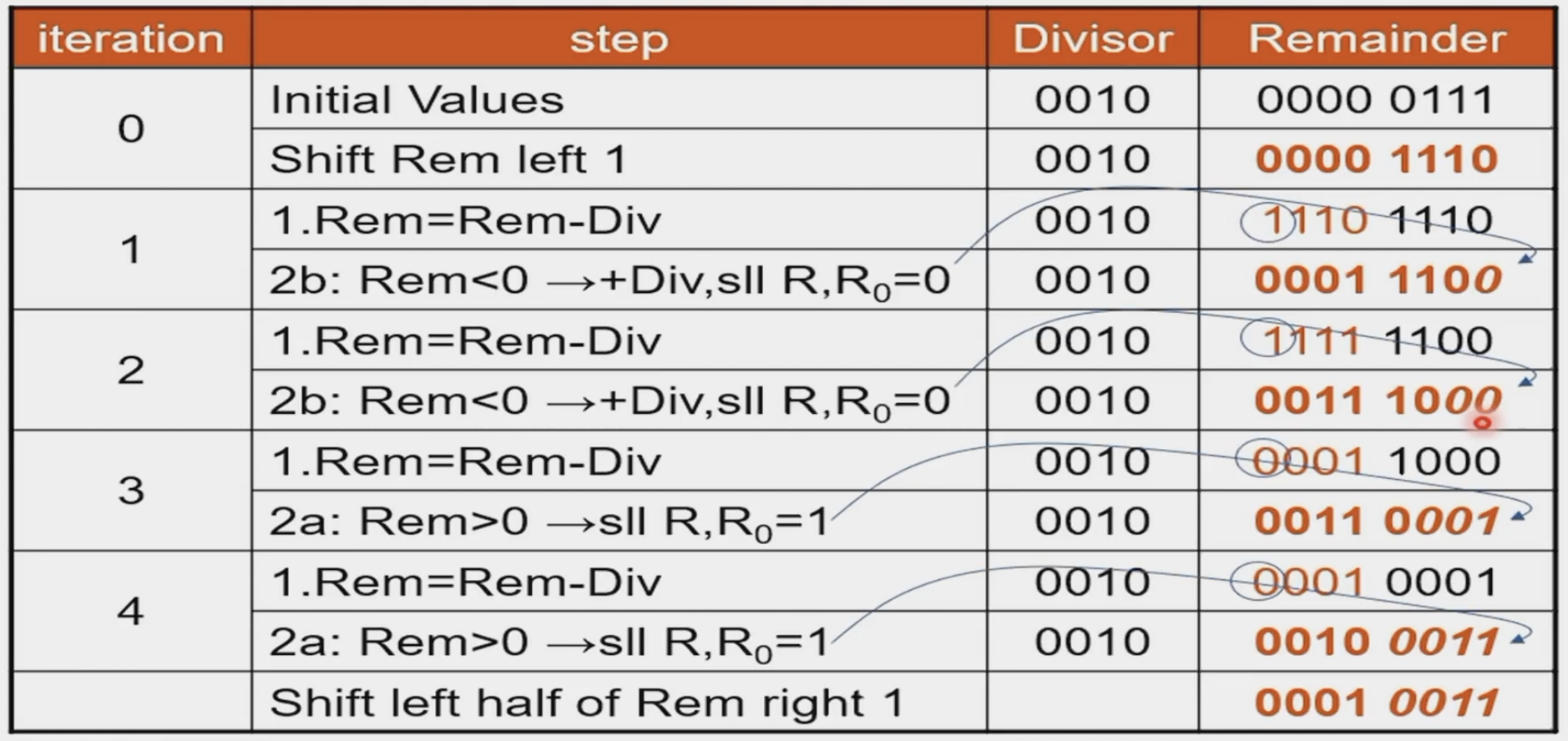
- Signed Division
Reminder 需要与被除数同号
Floating Point¶
32位处理器的数表示范围:
\(-2^{31} 到 2^{31}-1\)
浮点数的表示:
- Sign
- Significand 增加精确度
- Exponent 增加范围
二进制数的标准表示方法:
\(1.xxx * 2^{yyy}\)
对单精度浮点数,y有8位,x有23位
对双精度浮点数,y有11位,x有52位

第一位的1是一定的,因此不需要计入存储,Exponent是带有Bias的
单精度浮点数Bias为127,双精度浮点数Bias为1023
因此最后总的表示方法是:
0.75 和 -0.4375


- Single Precision Range
指数中 00000000 和 11111111 是特殊值
当Exponent为11111111,Fraction为00000000时,表示无穷大
当Exponent为11111111,Fraction不为00000000时,表示NaN(Not a Number)
因此单精度浮点数的范围是:
Smallest Number: \(1.0 * 2^{1-127} \approx 1.2 * 10^{-38}\)
Largest Number: \(1.111... * 2^{254-127} \approx 2 * 2^{127} \approx 3.4 * 10^{38}\)
每一位都是1的时候(1.111...),表示无限接近于2
Floating Point Arithmetic¶
- Addition and Subtraction
- Alignment
将两个数进行对齐,通常是将较小的数往大的靠近,因为如果将大的向小的对齐,损失的位数是更高的位数,损失的精度更多
-
Addition
-
Normalization
-
Rounding
0.5 + -0.4375

- Multiplication
相对简单,只需要将指数相加,尾数相乘即可。
除法也是类似的
Accurate Arithmetic¶
为了提高舍入的精度,IEEE 754 标准规定为浮点数额外添加 2 位,从左到右分别称为Guard和Round,这两位数字保留了浮点数计算的中间过程,从而尽可能地避免精度上的损失。
- Sticky Bit:Sticky 位用于记录移出的尾数中的非零信息,是指只要在Round右边出现过1,那么sticky位就为1
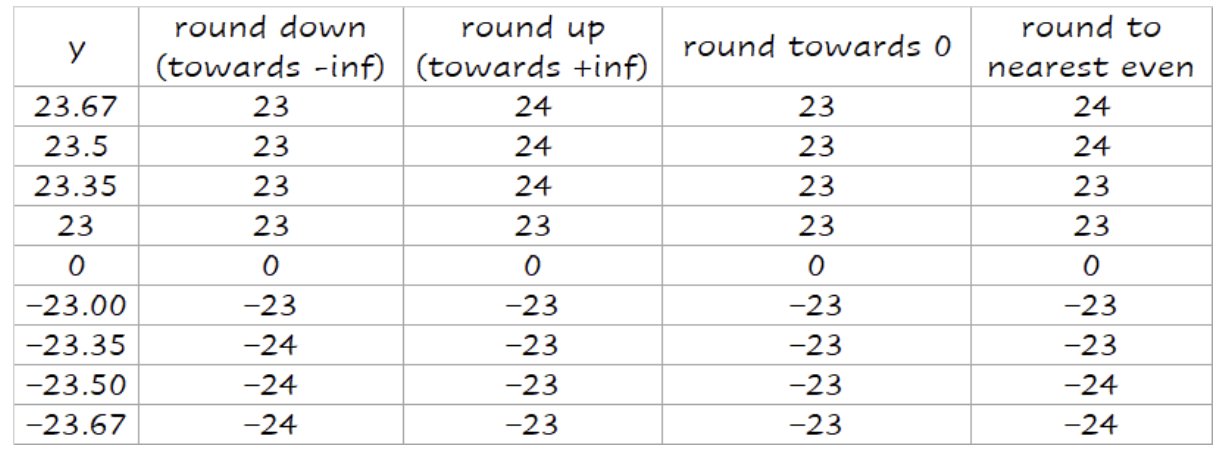
浮点数的舍入
- 如果Guard位为0,那么直接舍去Round和Sticky位
- 如果Guard位为1,Round位为1或者Sticky位为1:结果向上舍入,如果都为0,结果向下舍入(保持不变)
Example

留言