Database System¶
约 5985 个字 14 行代码 98 张图片 预计阅读时间 20 分钟
摘要
这是我在学习数据库系统时的memo,我不会系统的整理整个课程的笔记,但是会写下一些备忘和例子方便复习时使用
Relational Model¶
- 关系的定义最基本是集合,集合是没有重复元素的
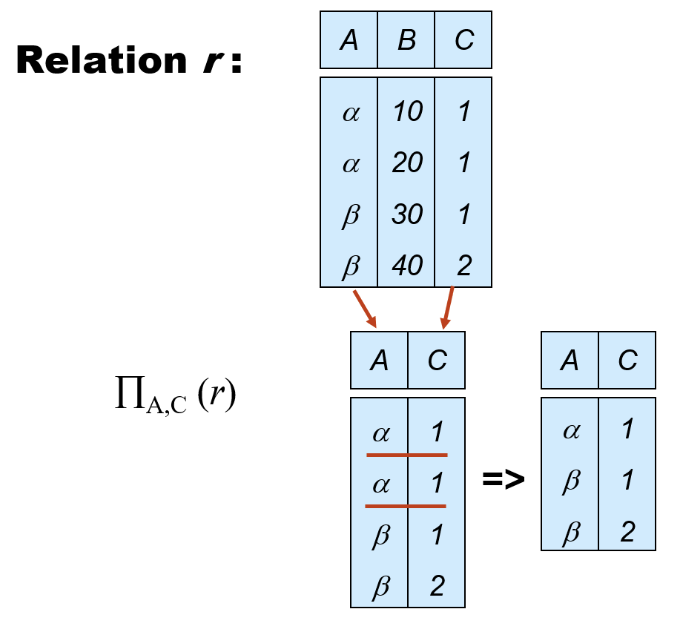
mutiset 是允许重复元素的
-
Union 中要求:
- 两个集合的arity相同(same number of attributes)
- attribute domains 是要compatible的,不是说完全相同,但是要类似
-
Rename:
重命名中的E不一定是关系,也可以是表达式
-
Natural Join:
没有增加表达能力但是简化了操作,可以用基本操作代替:
- 笛卡尔积
- 选择共同属性相同的部分
- 投影
还有一种left outer join \(\mathbin{⟕}\),是笛卡尔积后选择,如果属性不同,就用null来填充
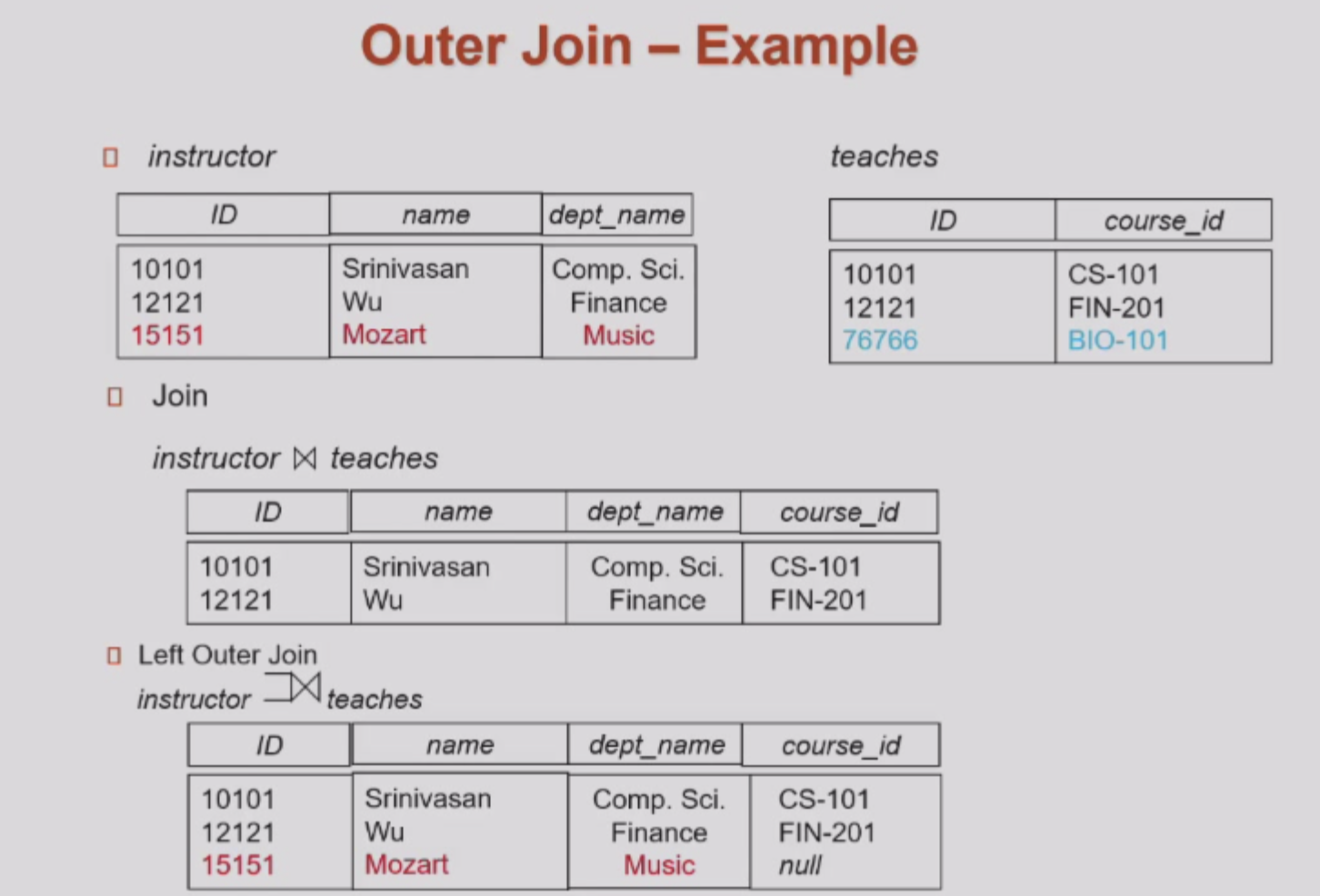
同理还有right outer join \(\mathbin{⟖}\),left outer join的镜像,以及full outer join \(\mathbin{⟗}\),两个的并集:
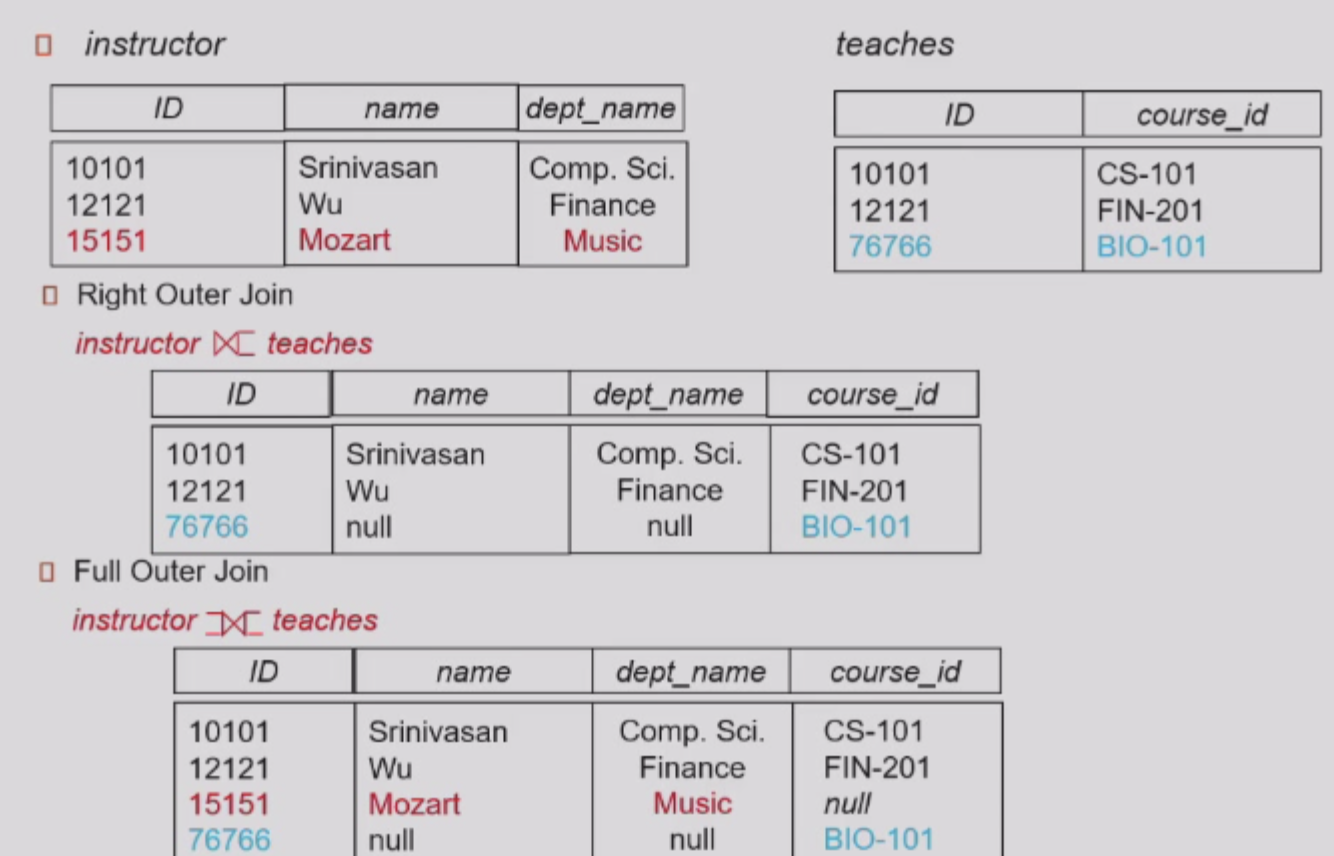
-
Semijoin:
用符号\(\ltimes\)表示,是natural join的子集,只保留natural join后左边关系中的属性,同理也有\(\rtimes\),是right semijoin,保留右边关系中的属性:

-
Division:
用符号\(\div\)表示,对\(r \div s\),要求:
- \(s\)是\(r\)的子集
- \(s\)的属性是\(r\)属性的子集
结果是包含\(s\)属性的对应\(r\)的元组:
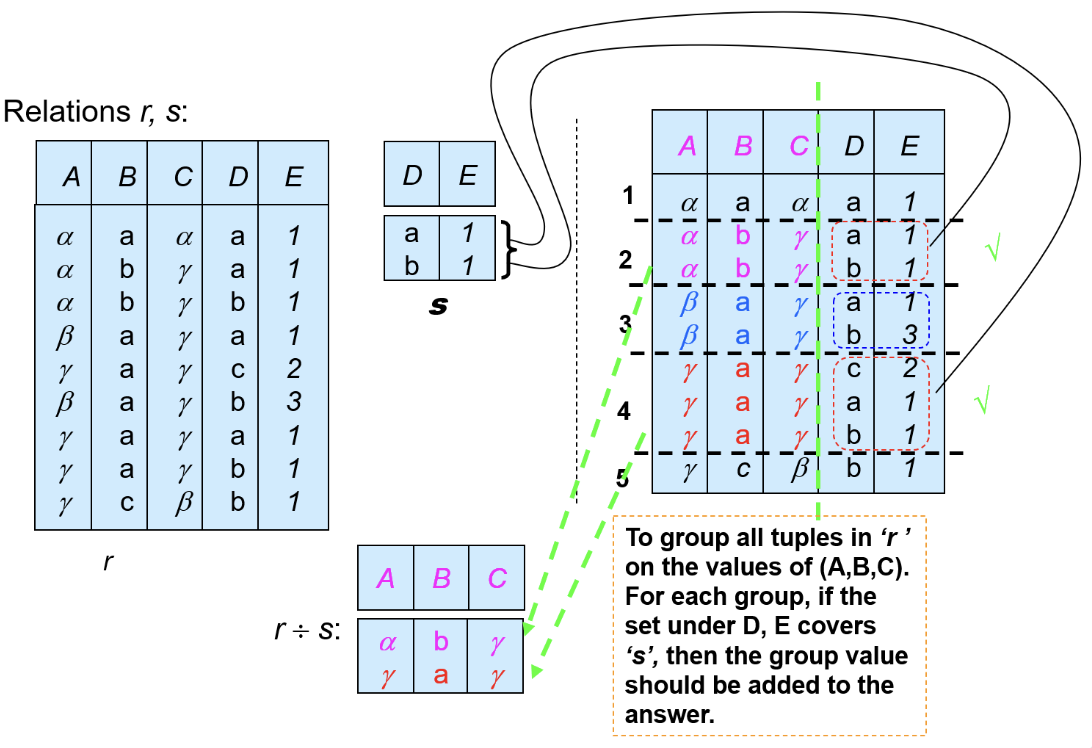
用处:

-
Multiset:
多重集,允许重复元素(去除重复元素代价很大)这样就支持SQL中操作
Intro to SQL¶
-
interval:period of time
- 用两个时间做差
-
create table 来个例子:

create table只是在定义一个schema,需要在后续的如insert操作中创建instance
- Integrity Constrains

-
foreign key
对于foreign key,要求在主键中存在,或者为null,但是如果一个操作导致foreign key指向的对象被删除,会有以下可选项:
- on delete cascade: 级联删除,将有关的全部删除(系没了学生也删掉)
- on delete set null: 设置为null(系没了学生还在但不知道系名)
- on delete restrict: 拒绝删除(系里有学生,系就不能删)
- on delete set default: 设置为默认值(系没了,学生还在,设置到默认的系中)
同样对于update,也就是被引用的对象的更新,也有on update+四个一样的选项,只是这里的级联是更新所有引用者的值
-
alter table
支持动态更改表的定义
- group by
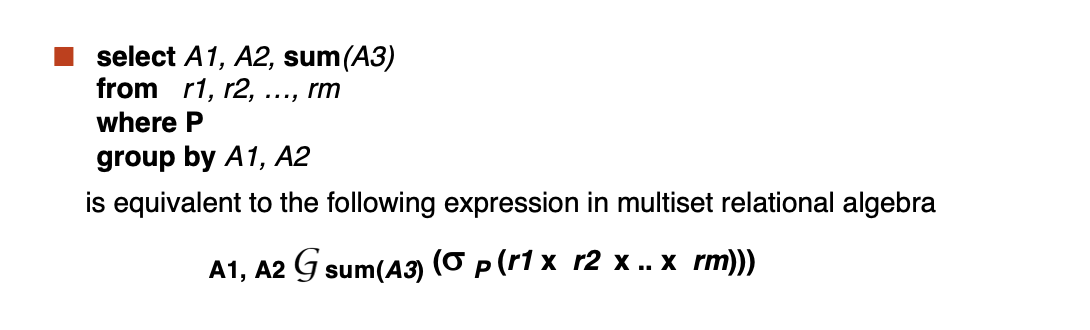
- natural join
简化操作

- 通配符

中文字符占位是两个字节,有可能出现前后两个字中间的部分被截断匹配的情况,因此中文建议完全匹配或者用 _ _ 来表示一个汉字
- limit
用于控制返回的行数
- not exist的一个例子

Intermediate SQL¶
- 连接表达式
连接条件之前的表达式中这样写:
现在可以采用join using来写:
join on
虽然看上去on的作用可以被using和where代替,但是在使用outer join时,on可以起到作用
- 使用outer join的一个例子:

通过outer join解决:保留左边关系中的没有课程的学生的ID,其余信息null

如果使用的是where:

也就是说outer join只是对结果关系进行的补充,而不是对参与连接的关系进行补充,因此在使用where(作用对象就是参与连接的关系)时,上述例子会出现根本找不到Snow这个学生的ID,where就会过滤掉Snow的信息
连接类型可以和连接条件组合使用:

-
事务 trasaction
-
完整性约束
-
用户定义类型
create type dollars as numeric(12, 2) final; /*final 表示是最小的类型,不能被继承*/
create table sales (
id integer,
amount dollars
);
- Domain 类型定义
domains与type相比可以添加约束,比如:
- Large Objects Types
图像、视频等大体积文件被存储为大对象类型
- Authorization
角色是权限的集合
Advanced SQL¶
- Procedure and Functions
Design and ER Model¶
- Attribute
复合属性:对应的组件属性会紧放在复合属性的下方,并且开头有缩进
多值属性:被花括号包裹
派生属性:末尾有圆括号
- Cardinality
用横线上的lh来表示全连接、单射

- 关系集的主键
我们需要确保得到的关系是唯一的,因此需要通过选取一个或多个属性来确保唯一性,这个属性或属性集被称为关系集的主键
所以在多对一多对多等问题中,只需要思考怎么让关系集唯一即可
- 三元关系中,不能使用超过一个箭头
原因就是在唯一性这里:

可以看到有两种结果
解决这个问题有两种方法:一种是将关系集转变成实体集,另一种是使用函数依赖
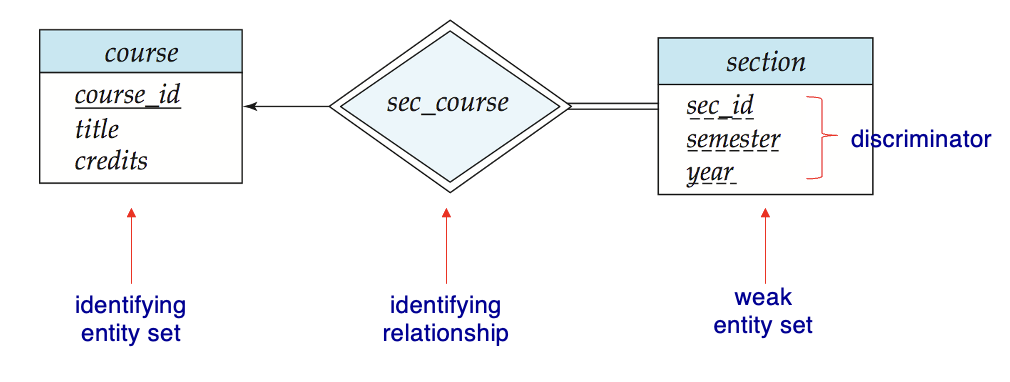
- Weak Entity Set
我们在建立section和course之间的关系sec_course时,发现如果sec_course中保留了course_id,那么其实section中也有,这样就十分多余,如果不保留这个关系,那么section和course之间的关系就无法建立
我们将section中的course_id去掉,然后建立section和sec_course之间的关系,现在面临的问题是section不具有唯一性了,这时我们定义section为弱实体集,他的唯一性由两点因素决定:
- identifying entity set:在标识性实体集中选择主键
+
- discriminator:一些附加的用作区分的属性
然后连接强弱实体集的关系就被称为identifying relationship
- Redundant Attributes
对于组成属性,直接写最小子项,中间项不保留:

对于多值属性,有一个特殊情况:

直接转换的话,得到的是两个关系集,一个是time_slot,一个是time_slot_detail,可以选择不要前者,但是这样就无法定义section的外键
- Design Mistakes
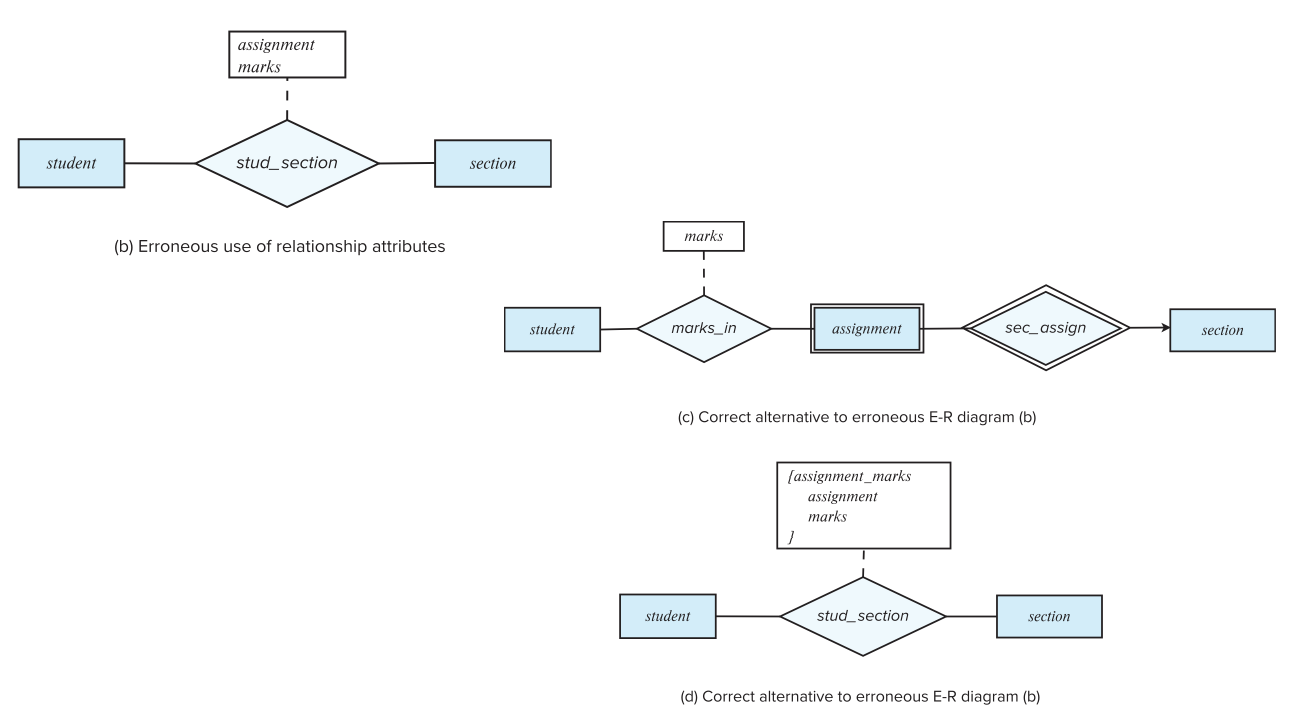
assignment不能是一个数值,应该是多值的,有右边两种方式改正
Extended ER Feature¶
Relational Database Design¶
这章的内容有点多,我进行一个梳理:
- Features of Good Relational Design
- Atomic Domains and First Normal Form
- Decomposition Using Functional Dependencies
- Functional Dependency Theory
- Algorithms for Functional Dependencies
- Decomposition Using Multivalued Dependencies
- More Normal Forms
- Database-Design Process
- Modeling Temporal Data
总体的思路是:

Features of Good Relational Design¶
- lossless decomposition

Atomic Domains and First Normal Form¶
原子化的域是指不能再进行分解的,FNF就是指每个属性都是不可分解的,一个例子就是CS1102,表示计算机系11年的02号课程,可以被分解为三个属性,另外一个需要注意的例子是,the set of all sets of xx(int, string),表示所有int和string的集合,这就是non-atomic的了
Decomposition Using Functional Dependencies¶
Define functional dependency:

由箭头左侧能够完全决定右侧即可
- superkey和candidate key的定义如下:

这里需要注意的是K需要是某个属性的闭包,也就是K+能不能推出所有属性
也就是说candidate key是superkey中去掉一个属性后不再是superkey的子集的集合,可以称为minimal superkey
当然如果K+可以,那么K也就可以,并且K是最小的话,K就是candidate key
- trivial 的定义和性质:

左边囊括右边,一定是trivial
-
Closure
-
依赖闭包:这里的闭包和离散数学中的类似,就是计算函数依赖的扩展,在这里计算时要用到几个律:
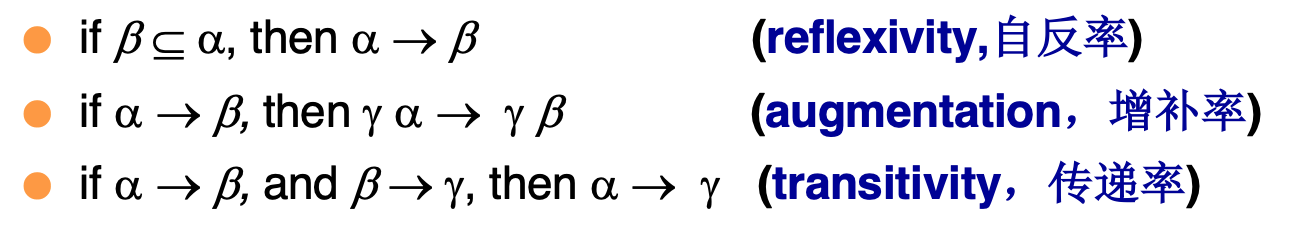

- 关系闭包:这里是计算在一组函数依赖下,一个属性能推导出的所有属性

Example

Tip
几个好用的性质:

第一个讲过了,第二个就是验证用trivial性质来反向推到依赖,比较方便
第三个就是可以有条理的计算出依赖闭包

先写出所有关系的组合,计算每个组合的闭包,再将他们展开
Functional Dependency Theory¶
- Canonical Cover
计算一个依赖集的minimal:
首先确定什么依赖是多余的:

验证一个属性是否在依赖中多余的方法:

计算一个依赖的最小覆盖:

Example

当然这道题可以通过更直观的方式观测出结果,不使用transitive,那么只剩下了两个依赖
Exercise
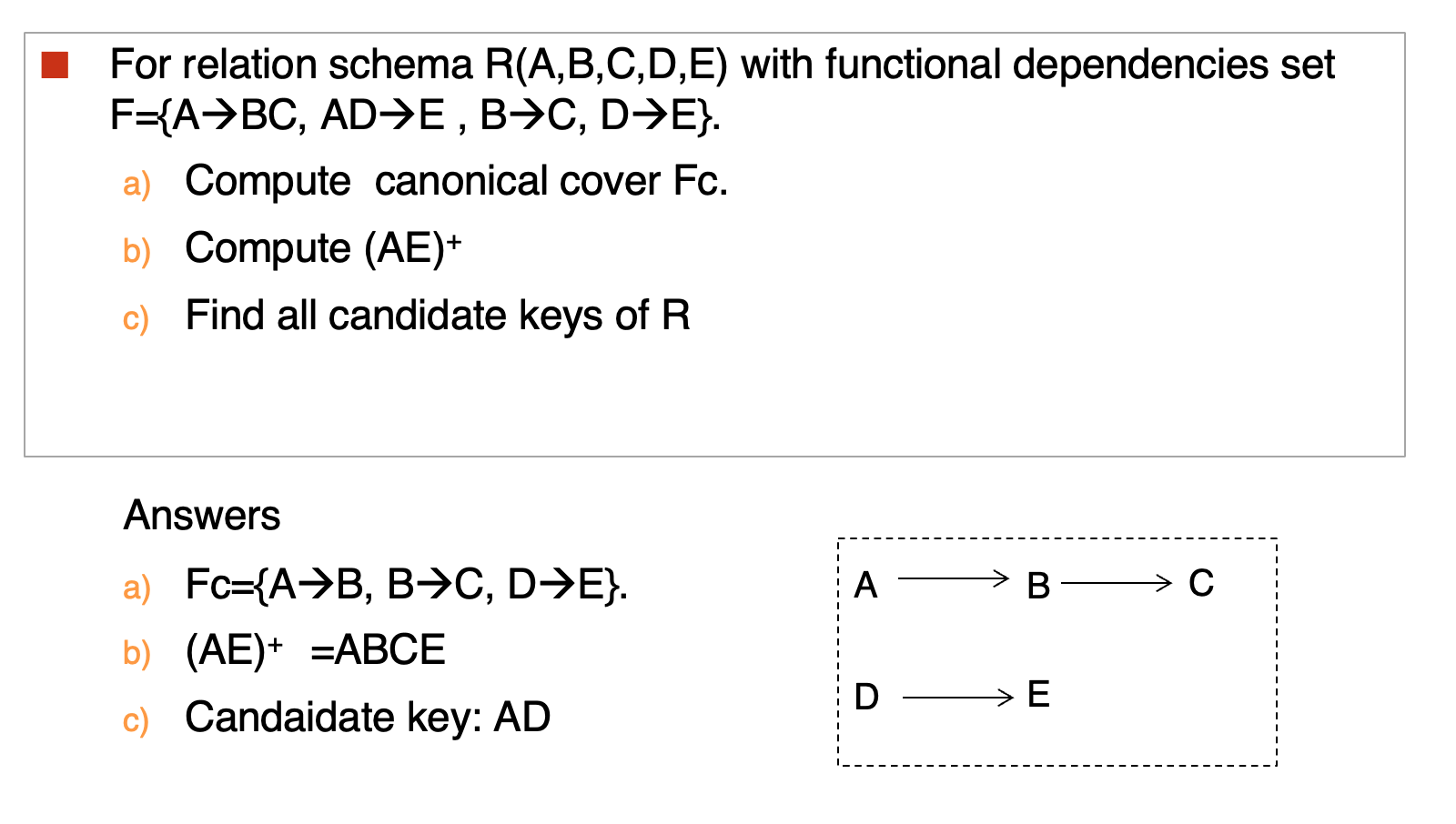
Algorithms for Functional Dependencies¶
进行范式的介绍并使用范式进行分解,这里与教材的方式不太相同,教材是开篇就介绍范式,这里孙老师先在前半部分把工具介绍清楚,这里就能在介绍范式后直接将范式分解
- BCNF

如果有不符合BCNF的,进行分解

Algorithm:
这个算法对关系进行分解:
找到一个不符合BCNF的依赖(左边不是superkey的),然后进行如下分解

Example
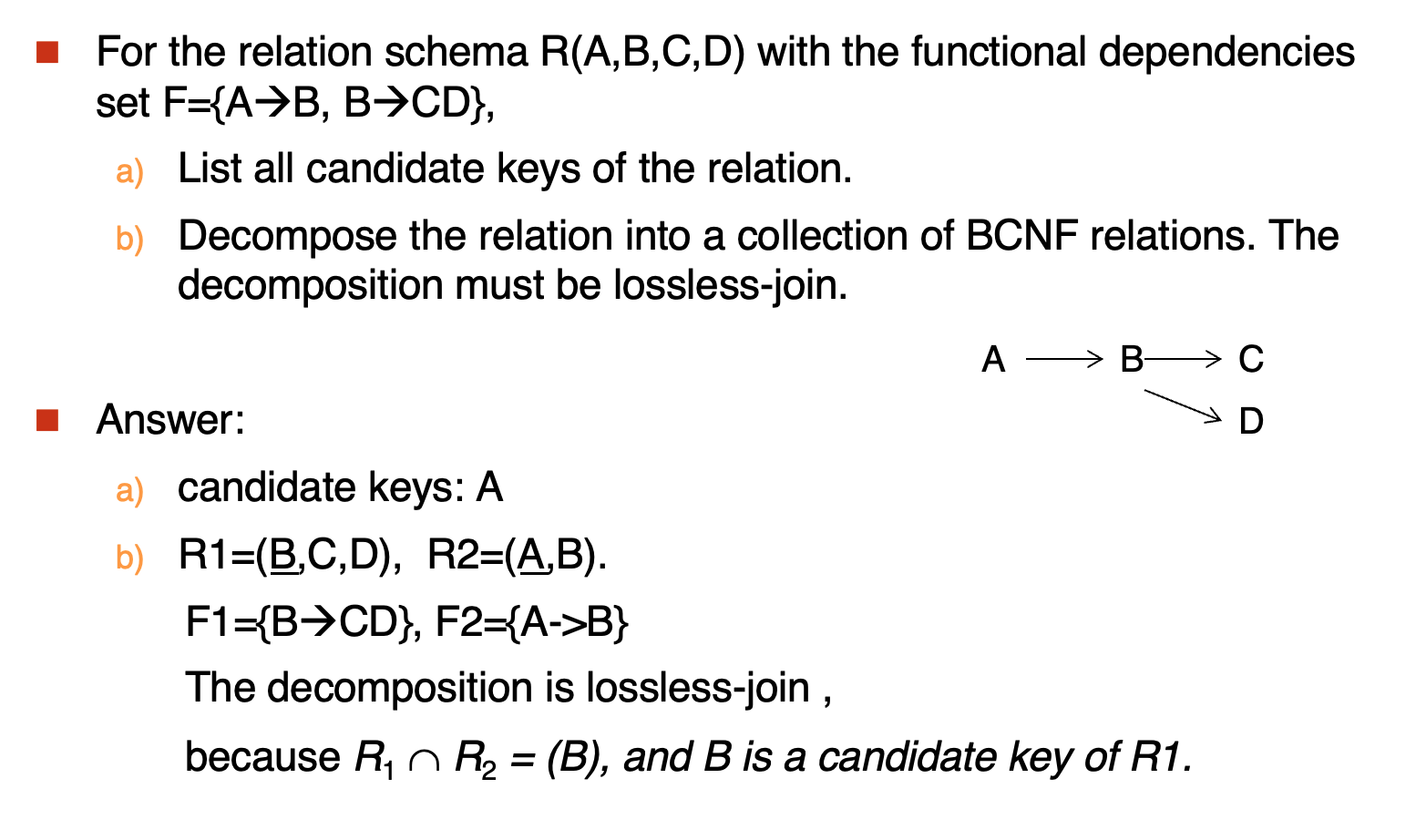
- Dependency Preservation
就是看一个依赖集在被分解后的并集是否与原依赖集相等
Example

如果 \(F\) 内的每个成员能够在分解中的某个关系上被检查,那么说明这个分解保留了依赖。但这种方法并不总是有效,因为即使分解是依赖保留的,但是可能会出现仅看其中的一个关系无法检测依赖的情况。所以这个方法只是一个充分条件
对于 \(F\) 中的每个依赖 \(\alpha \rightarrow \beta\),执行以下过程:
\begin{algorithm}
\caption{Alternative test for dependency preservation}
\begin{algorithmic}
\STATE $result = \alpha$
\REPEAT
\FORALL{$R_i$ in the decomposition}
\STATE $t = (result \cap R_i)^+ \cap R_i$
\STATE $result = result \cap t$
\ENDFOR
\UNTIL{($result$ does not change)}
\end{algorithmic}
\end{algorithm}
Exercise

BCNF不能保证得到的一定是依赖保留的分解,因此引入其他范式
- 3NF

如果左边不是key,那么右边必须是key的一部分
分解算法:

先得到最小覆盖,将覆盖里的每个依赖都进行分解,如果分解出来的关系中没有一条包含key,那么将key单独组成一个关系
Decomposition Using Multivalued Dependencies¶

Indexing¶
B+ Tree¶
Size Estimation

计算fanout:就是计算每个节点可以储存指针的数量,因为block size是4096,指针大小是4,并且比索引值要多一个(指向兄弟),所以4096-4,一个person信息需要18,再加上他对应的指针,(4096-4)/(18+4),最后再加上1即可

计算层高,可以用公式,也可以像上张ppt那样计算然后找到合适的区间
- max节点个数
计算半满(最浪费)的叶子个数,用1000000/93 向下取整,然后叶子上的一层也是半满,用叶子结点数/93 向下取整就ok
- min节点个数
计算半满(最节省)的叶子个数,用1000000/186 向上取整,然后叶子上的一层也是半满,用叶子结点数/187 向上取整就ok
注意如果是直接用B tree存储file,那么叶子结点就不需要有指针了(除了指向兄弟的),在计算个数的时候要区别一下
Query Processing¶
计量查询代价:
\(t_T\)是transfer一个block的代价,\(t_S\)是seek一次的代价,所以Cost for b block transfers plus S seeks:
Sorting¶
这里是外部排序被发明的地方
在这里我们使用N way merge sort,考虑的一是ADS中讨论的轮数,二是需要多少次block transfer&seek
M是buffer数量,N是内存中的归并段数量
- N < M时
归并段少于可用内存块,这时只需要一次pass
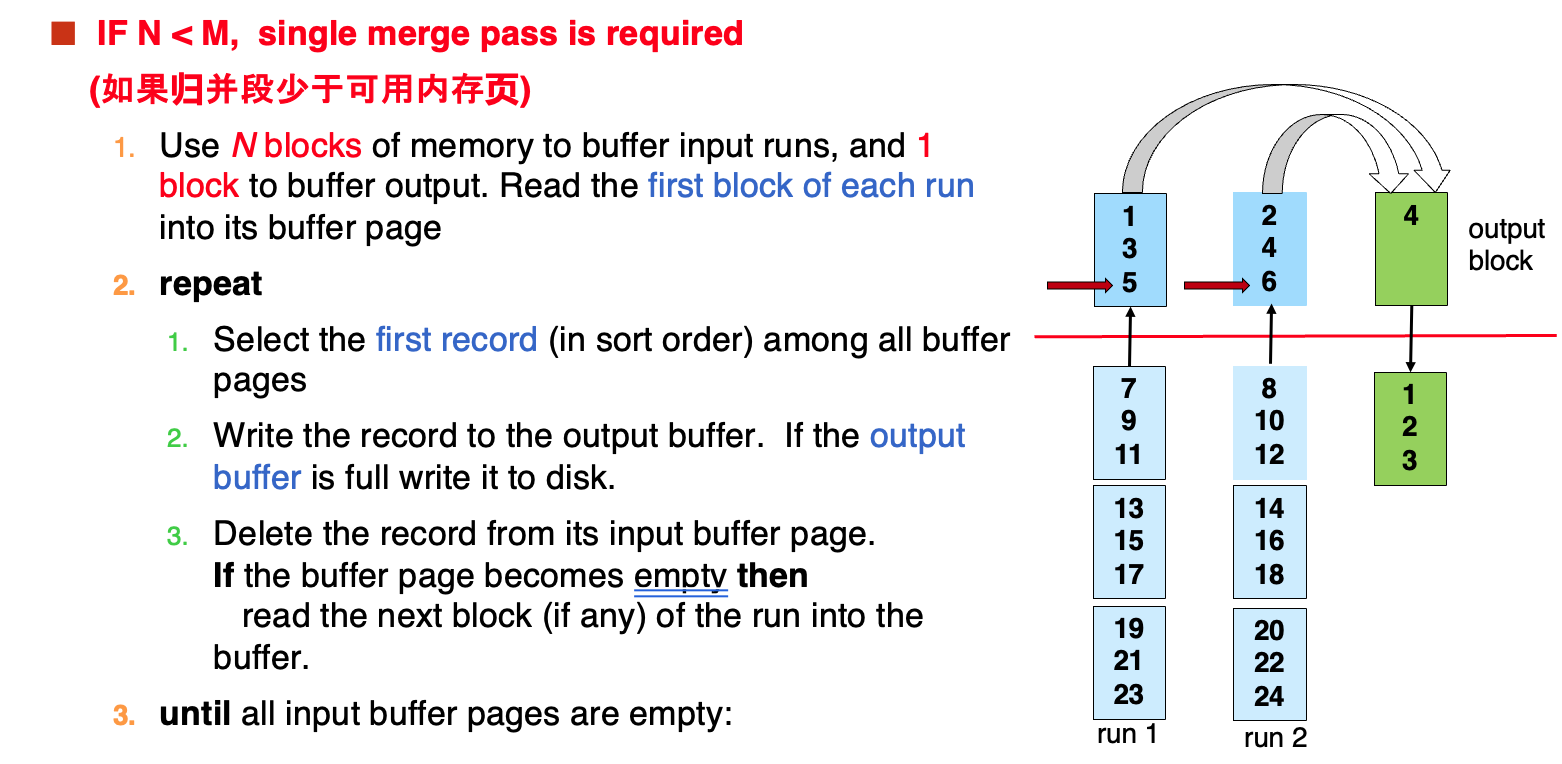
- N > M时
这时pass的次数就不是1了,虽然每一轮的代价仍然是一样的
有M块buffer可以用来归并,其中有一块是用来IO的,所以剩下M-1块,相当于是在做M-1 way merge
这时我们进行 transfer cost分析:

- 形成的归并段数量
- pass needed
- 生成归并段和merge时每一轮的block transfer
如果最后需要写出一次,那么最后的公式中应该是\(+2b_r\)(这里给出的是不写出的情况)
对seek cost的分析:

对于这个结果我们还可以进行一个优化,就是在归并时\(b_b\)个block进行merge
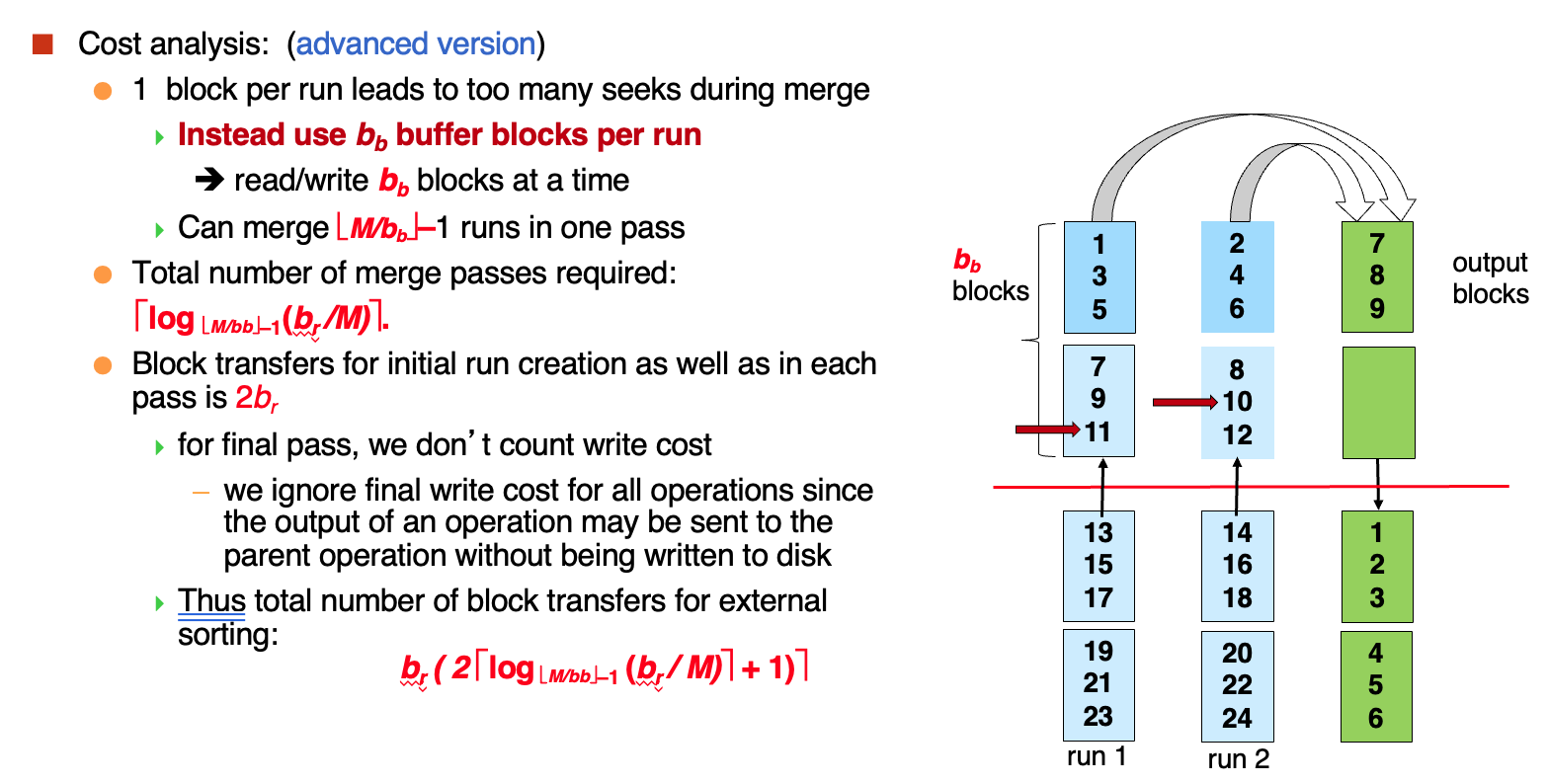
但是相应的每次可以merge的block数量就变少了,log的底数变小了
seek cost的计算:

Join¶
- Nested Loop Join
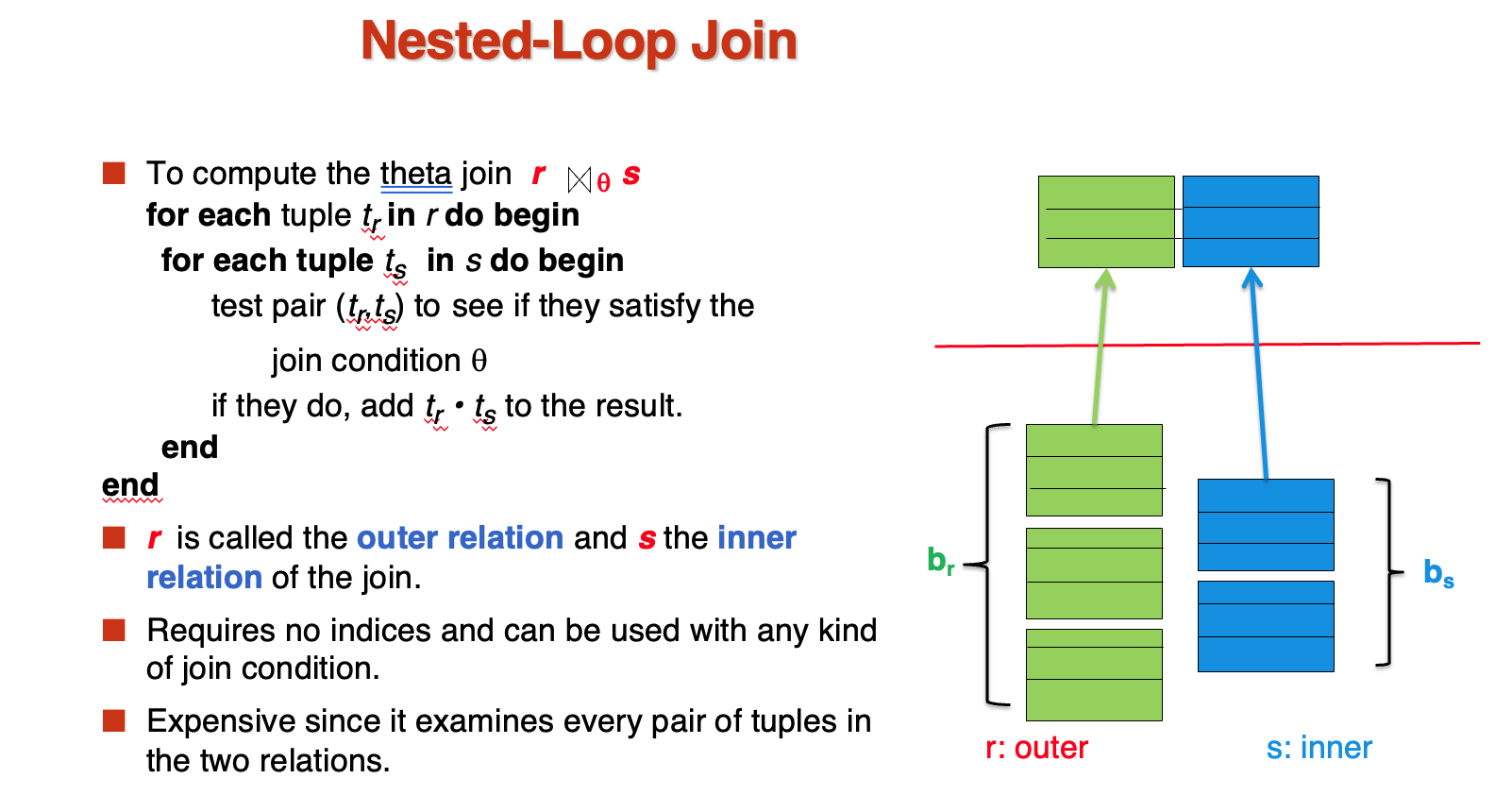
总共需要\(b_r + b_s*n_r\)的block transfer和\(n_r+b_r\)的seek
- Block Nested Loop Join
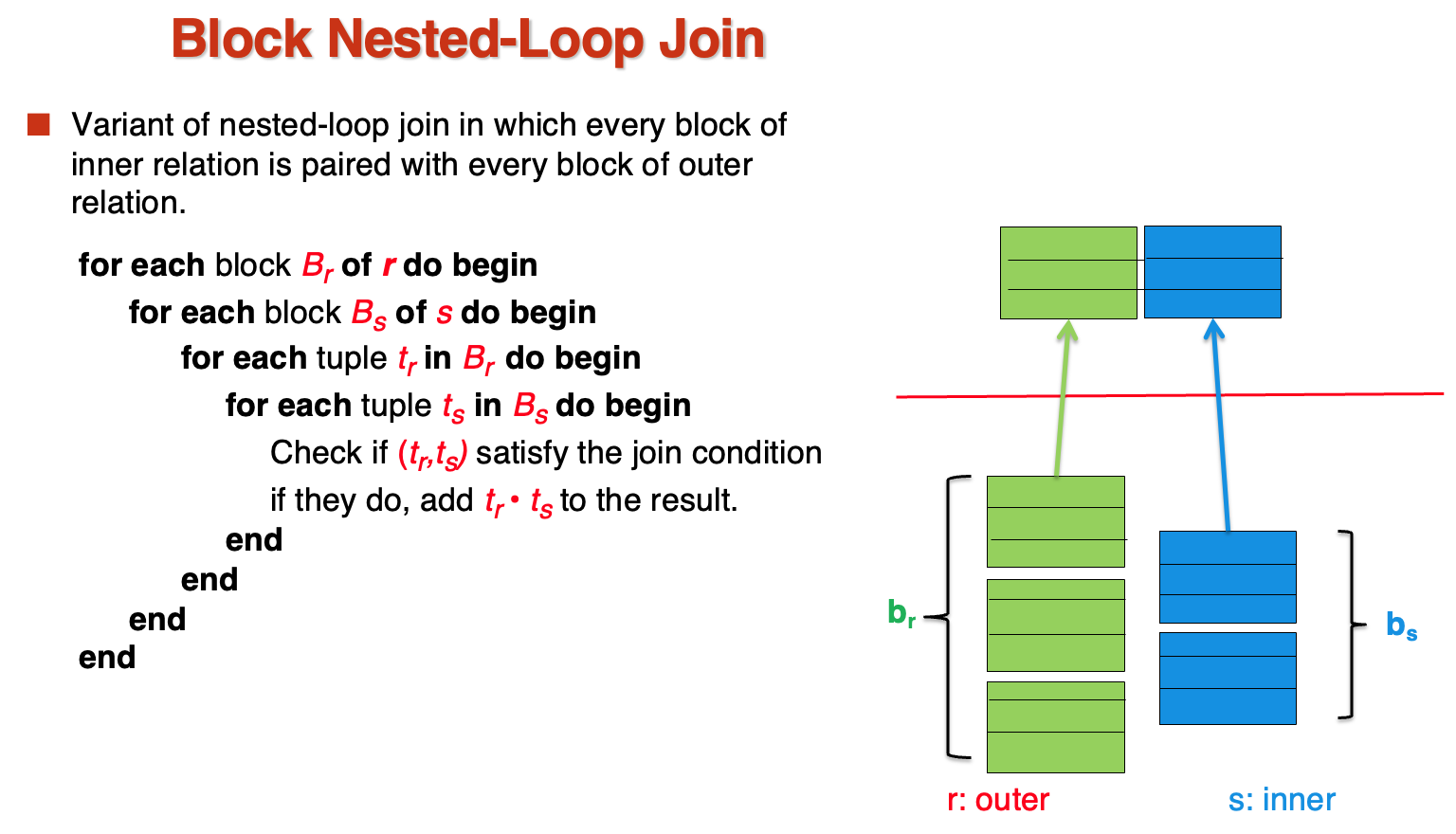
相当于是第一种方法的优化,将已经取出来的块在内存中进行比较,而不是直接比较所有元组
这时候的时间复杂度:

如果我们有M块buffer呢?
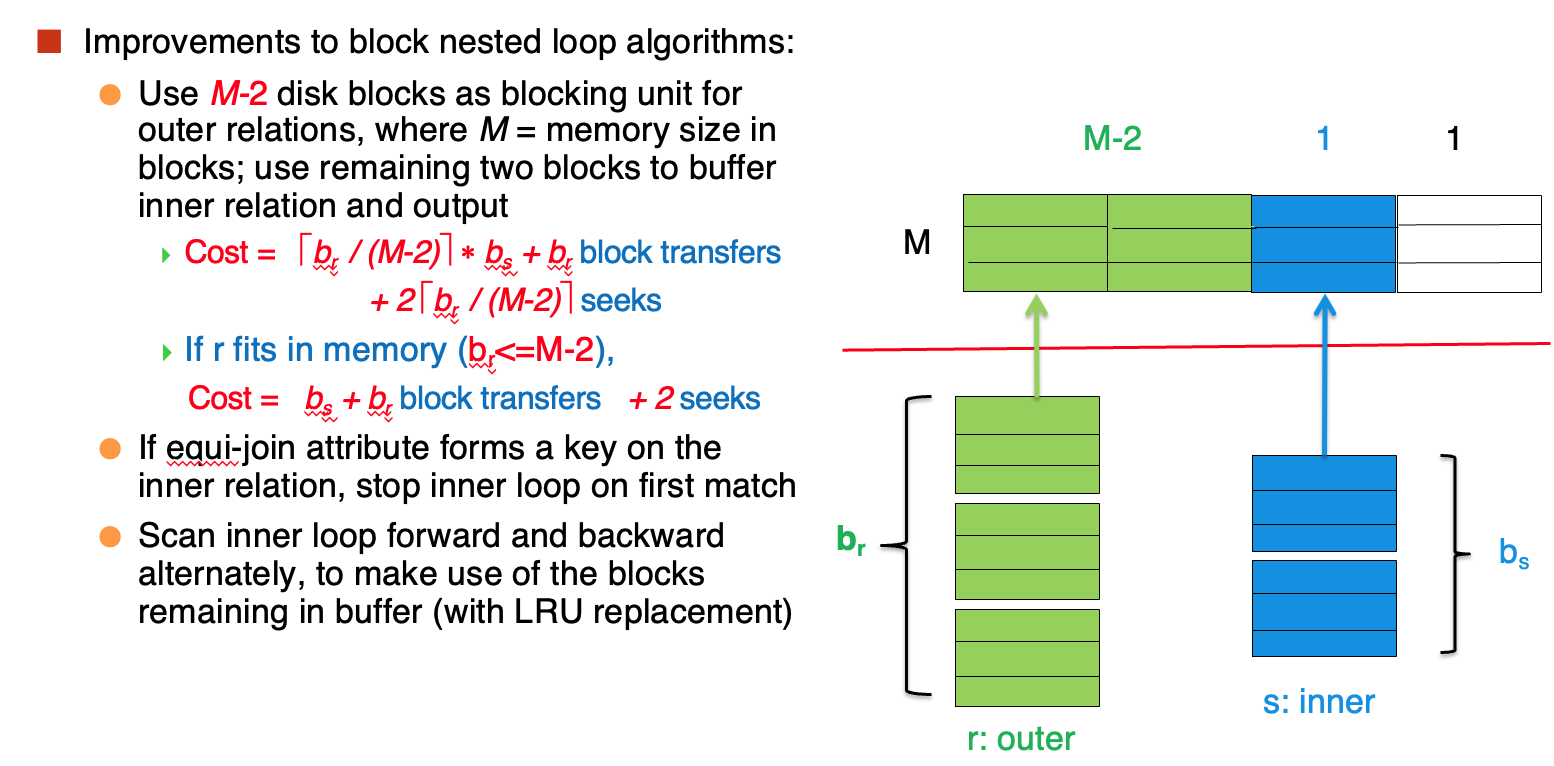
最后的白色块用作IO,用M-2块buffer存放outer block
- Index Nested Loop Join
现在inner relation是有索引的,就不再需要进行遍历来查找了,只要遍历outer relation,然后使用索引查找inner relation

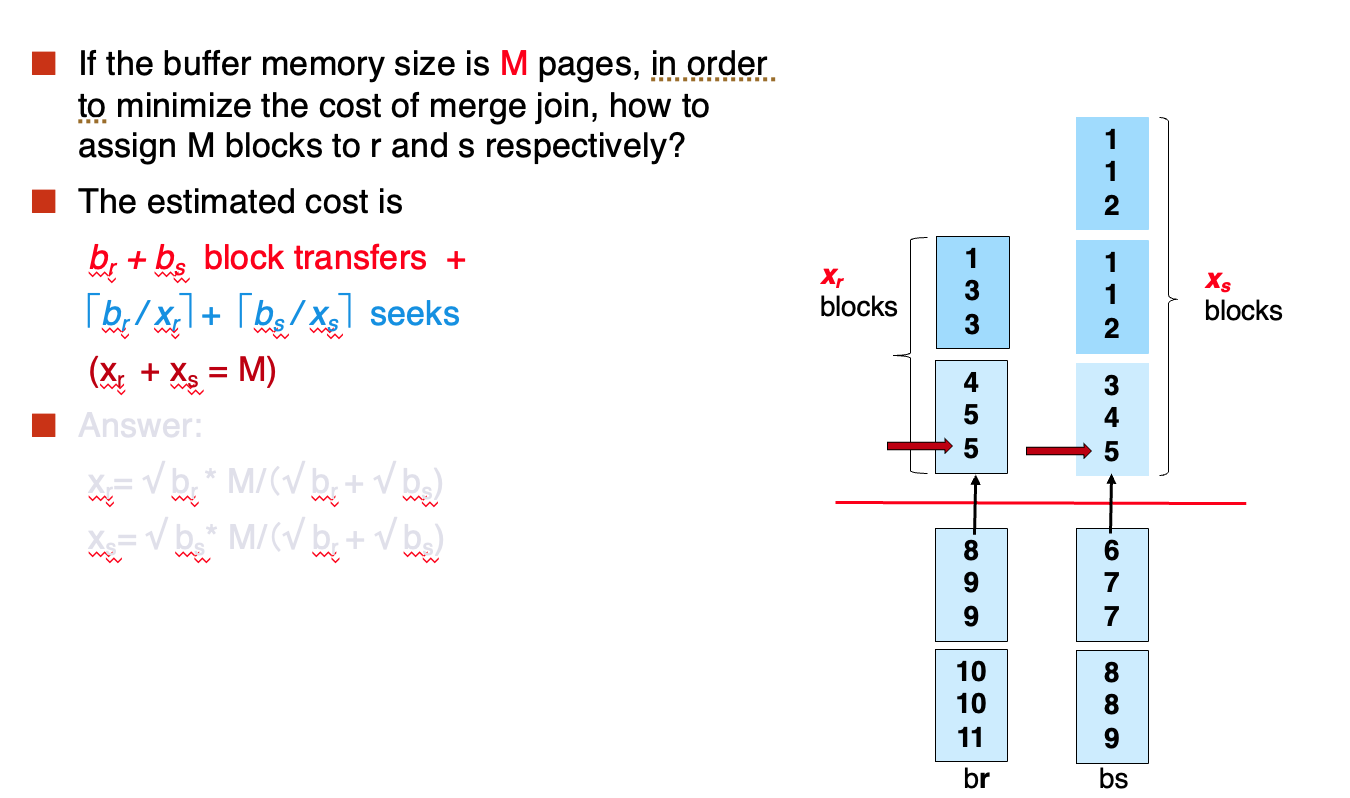
- Merge Join
采用多块进
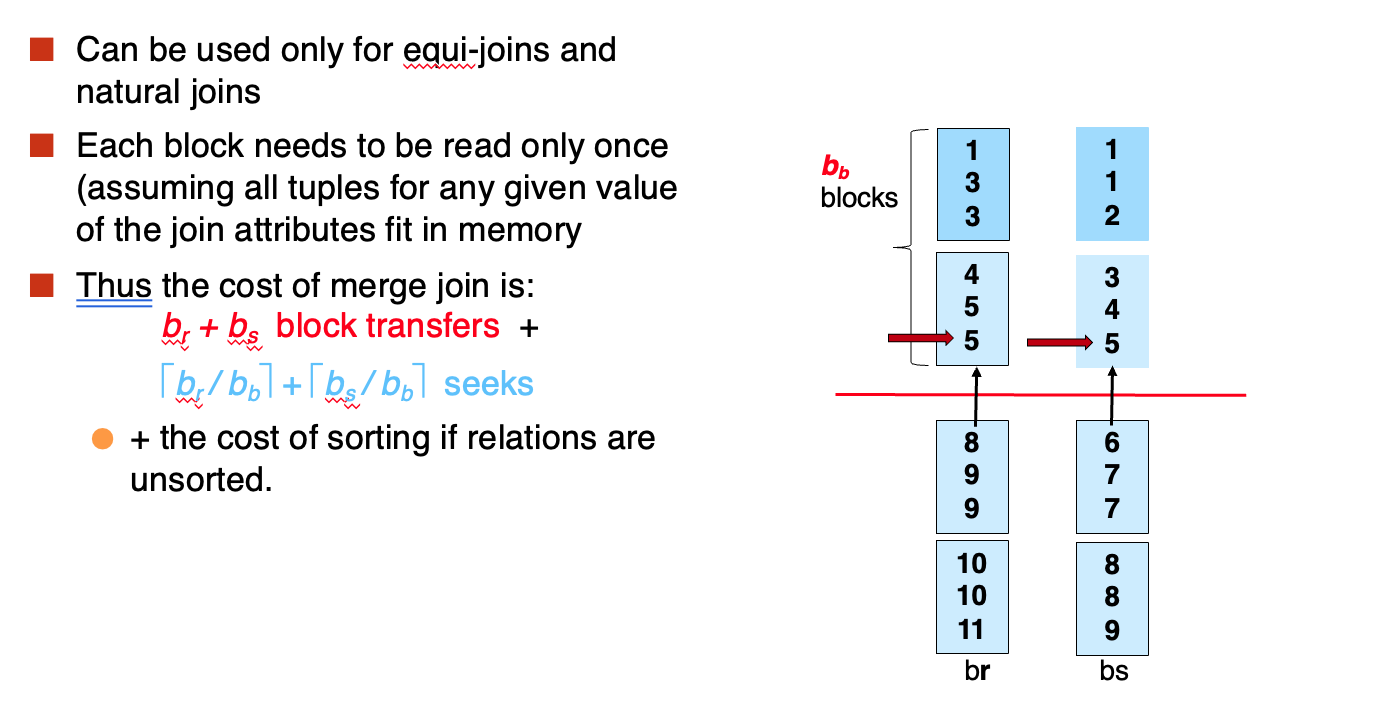
如果buffer的大小是M,我们要完全利用buffer:
- Hash Join
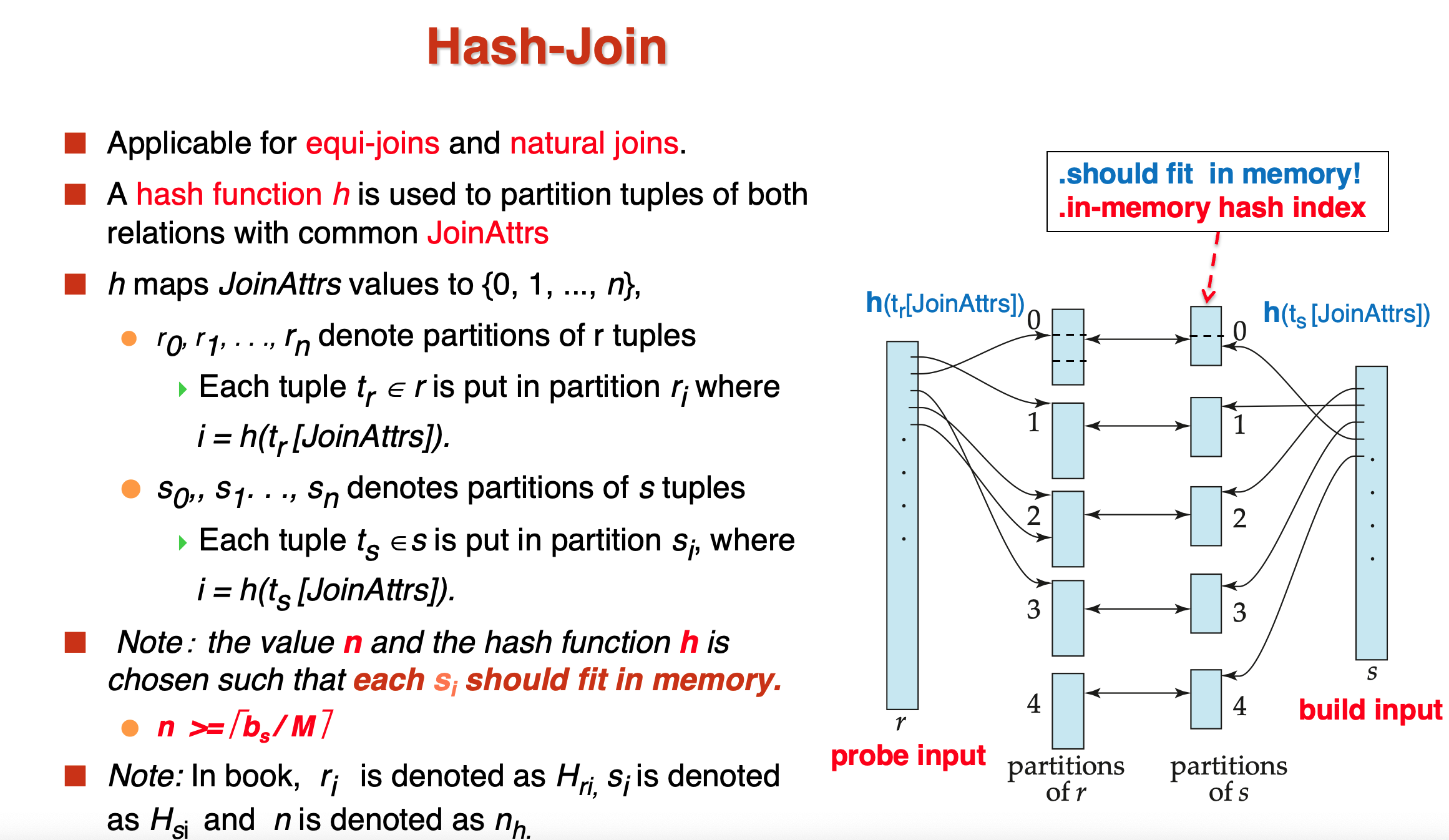
为了确保我们可以把build relation完全放进内存,\(n \geq\)这个数就是说至少要分成这么多个hash块
这样现在比较相同hash值的元组即可
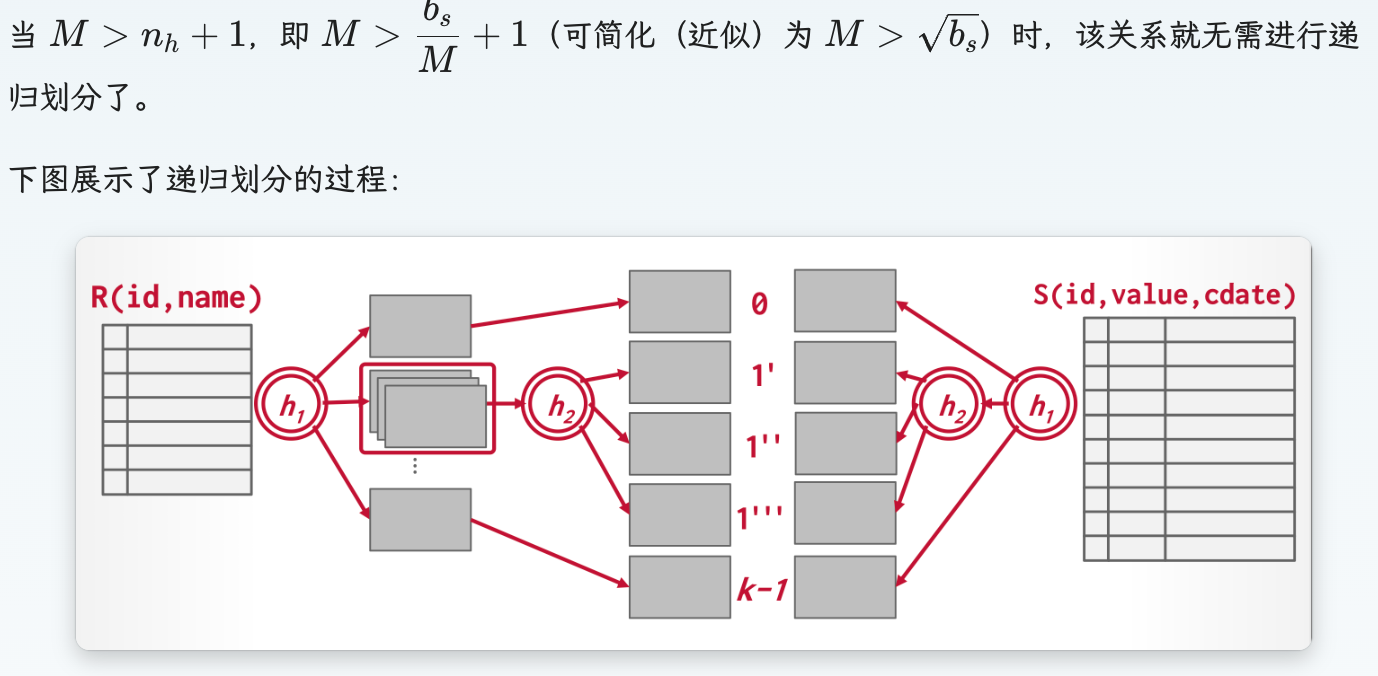
如果一次partition后的块数太多,就需要进行recursive hashing
Query Optimization¶
Cost Estimation¶
定义如下参数:

- Selection Size

- Join Size
如果两个关系的交是空的,那么自然连接就是笛卡尔积
主要讨论的是非空情况:
- 交是R的键:那么自然连接后的个数不超过S
- 交是由S指向R的外键:那么自然连接后的个数就是S的tuple数量
- 交不是两者的键

- Distinct Value
Cost-Based Optimization¶
使用左深树来表示查询树:
在进行分割的时候:

Optimizing Nested Subqueries¶

Materialized Views¶
Transaction¶
Model:
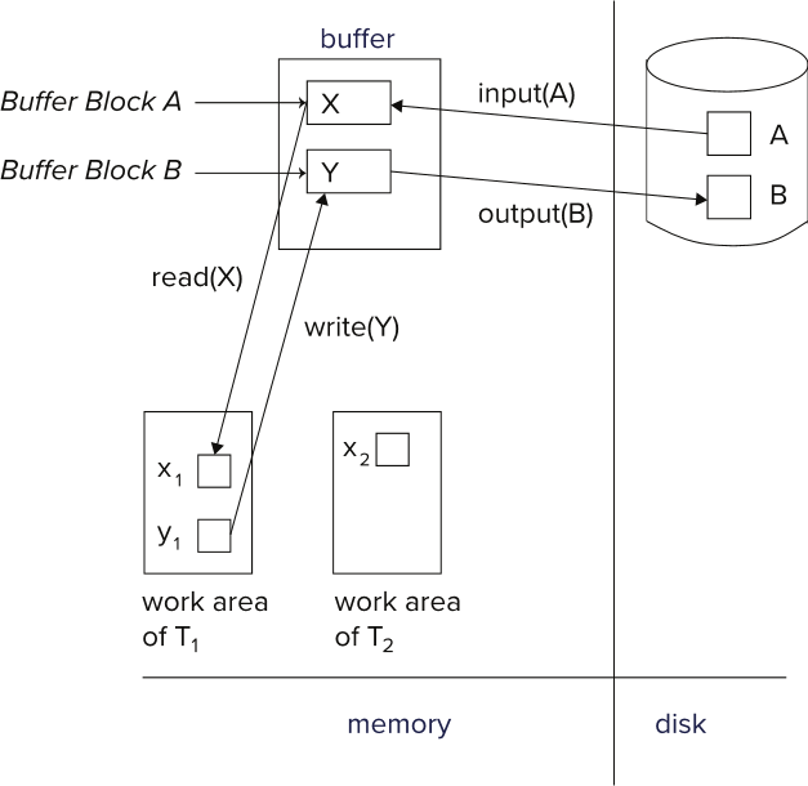
Outline:

-
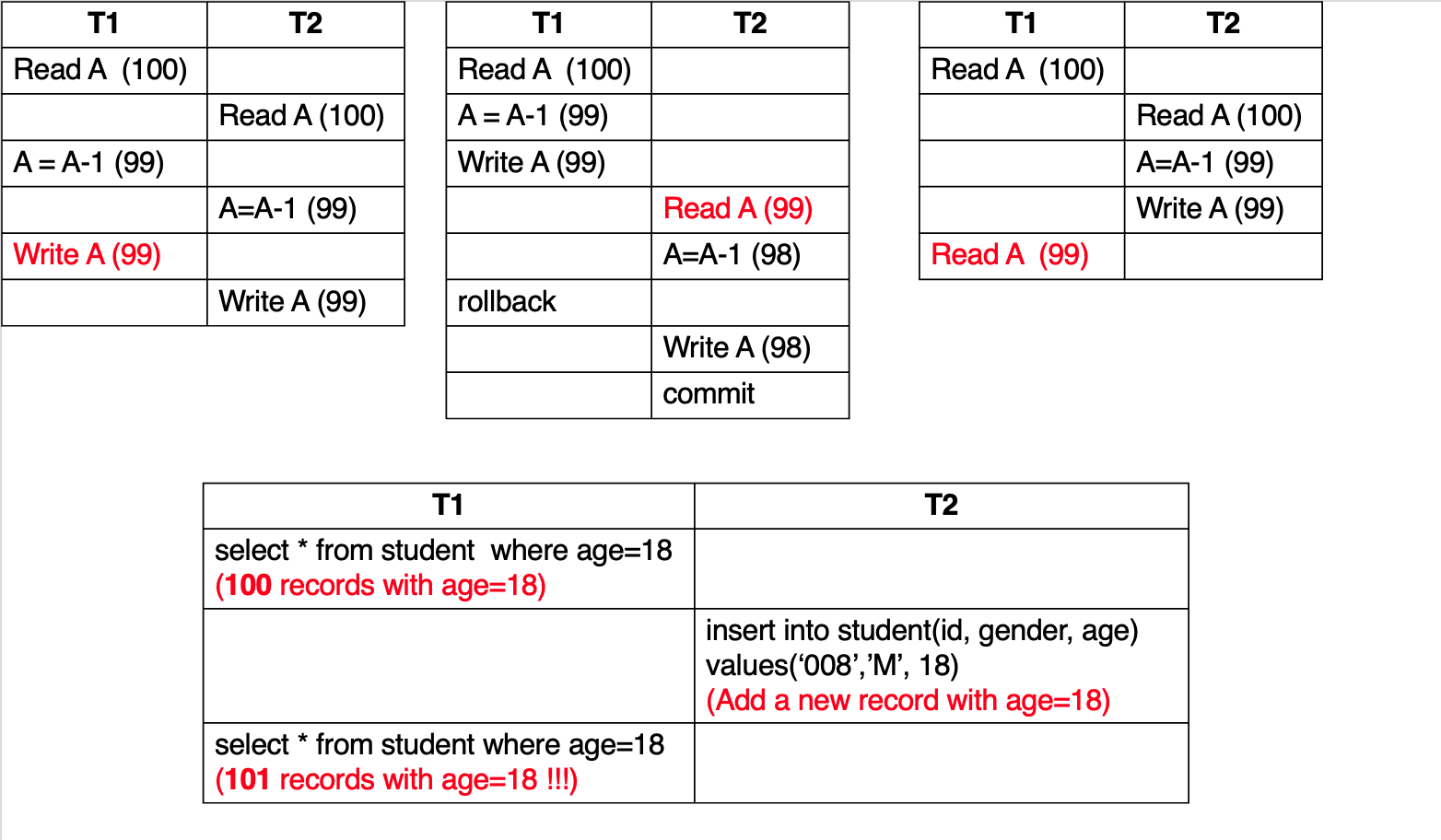
Anomalies in Concurrent Execution
一共有四种情况:
- Lost Update
- Dirty Read
- Unrepeatable Read
- Phantom Read
- Serializability
主要考察可串行化,注意这里的可串行化的定语,是基于冲突的conflict,还是基于视图的view
基于冲突的可串行化需要满足的条件是如果通过交换一系列不冲突的(no write)两个操作,可以将一个schedule变成一个串行的schedule,那么这个schedule就是冲突可串行化的
也可以通过别的方式检测:precedence graph
如果一个图是无环的(不能从某个点出发,经过一系列边,回到这个点),那么这个图是冲突可串行化的
如果一个节点(事务)是独立的节点,那么他可以被插入到任何事务前后(与其他事务相关性)

基于视图的等价:

视图可串行化讲究的是对同一个数据的操作有一致性
Example
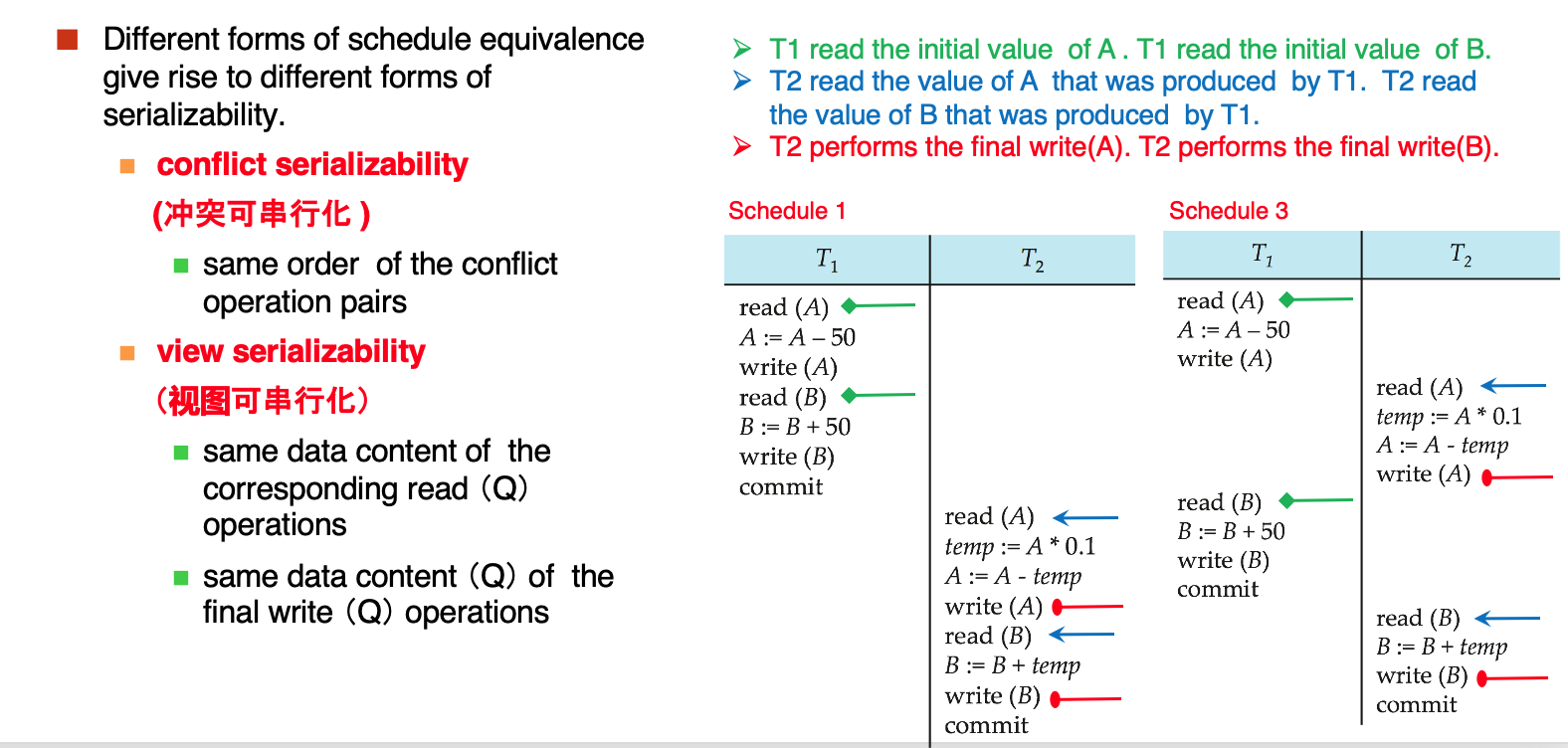
这里的三个颜色就分别满足了三个条件,对初始值,对中间值的顺序,对最终写
基于视图的可串行化:
如果一个schedule是关于一个serial schedule基于视图等价的,那么这个schedule就是基于视图可串行化的
- 基于冲突的可串行一定基于视图可串行,但是基于视图的可串行不一定基于冲突可串行

还有些其他的serializability:先前两种都不能进行等价

- Recoverable Schedules
可恢复调度保证commit的严格一致性
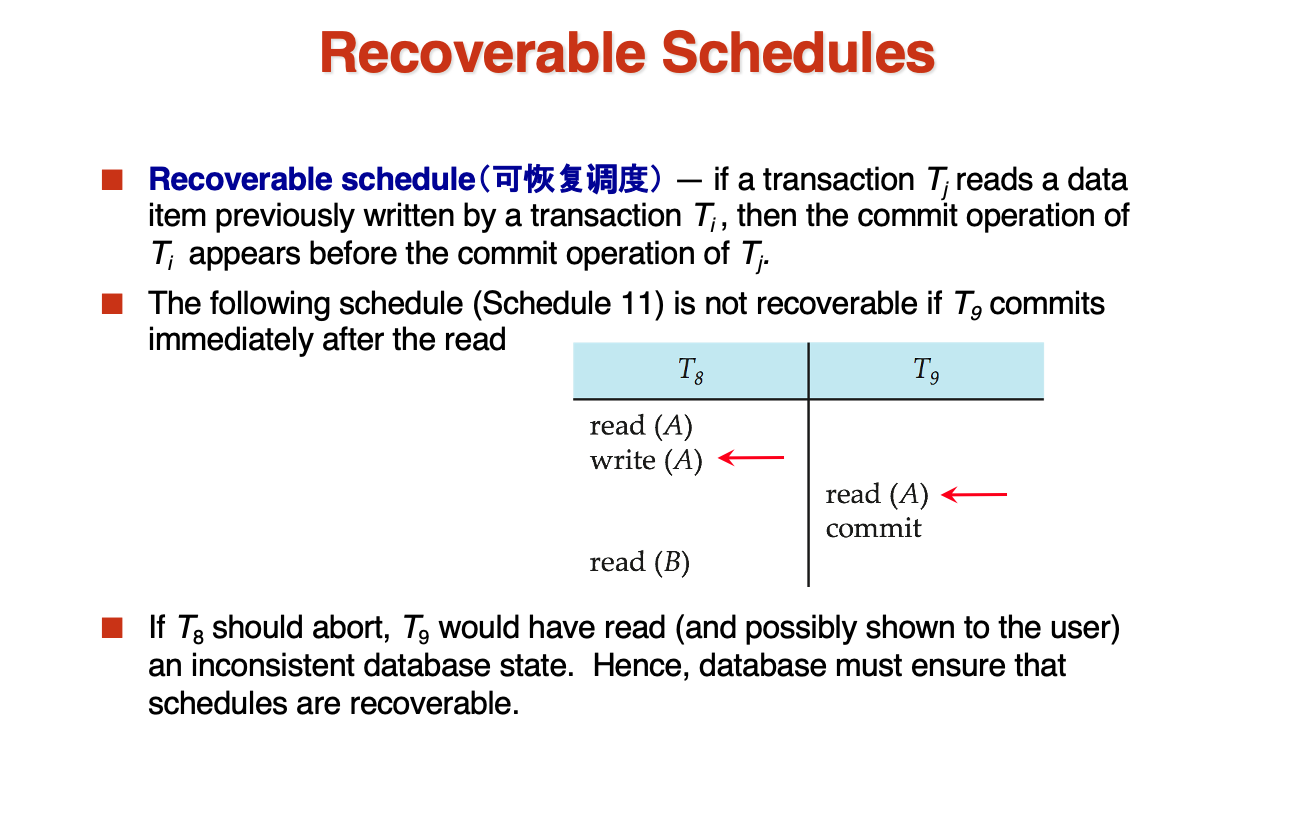
但是面对abort时,如果一个数据被一系列的动作修改,那么就需要rollback,往往这个rollback是cascade的,需要rollback一系列的修改,为了避免这种rollback,我们需要做一个cascadeless schedule

就是在一个事务写了某个数据后,下一项事务需要在这项事务commit后,才能读取到这个数据
Concurrency Control¶
- Lock-Based Protocol

- Two-Phase Locking
明确的两个阶段,一阶段是lock,二阶段是unlock,不能交叉
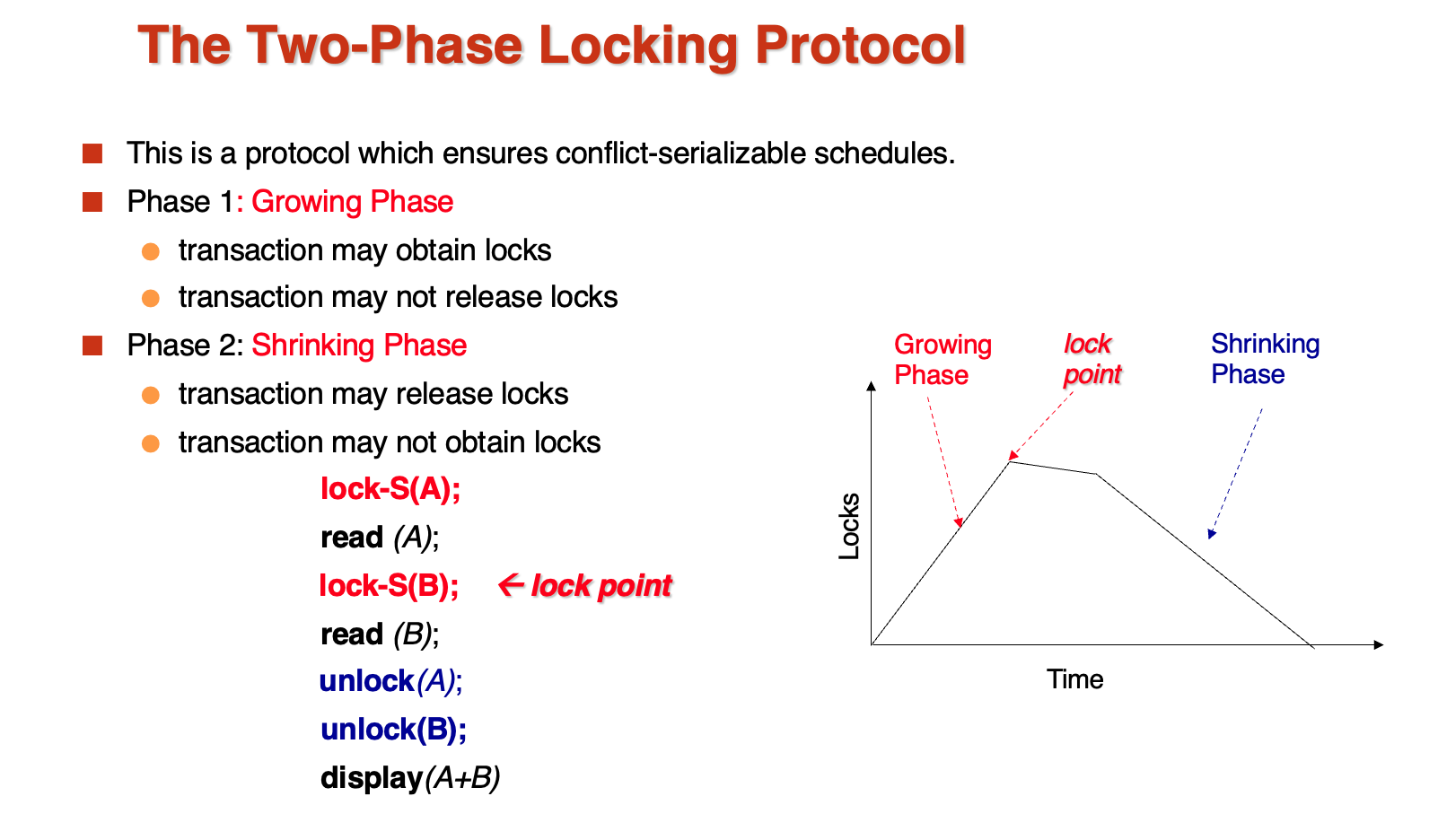
可以证明事务是冲突可串行化的,只要按照lock points的顺序进行操作
严格两阶段锁:确保X锁在事务提交前才释放
- Lock Table
table可以理解为一个hash table,每个接口对应一个数据,数据后接一个事务,表示当前的数据被哪个事务锁住了,如果有一个数据连着两个事务,说明这个锁是shared的
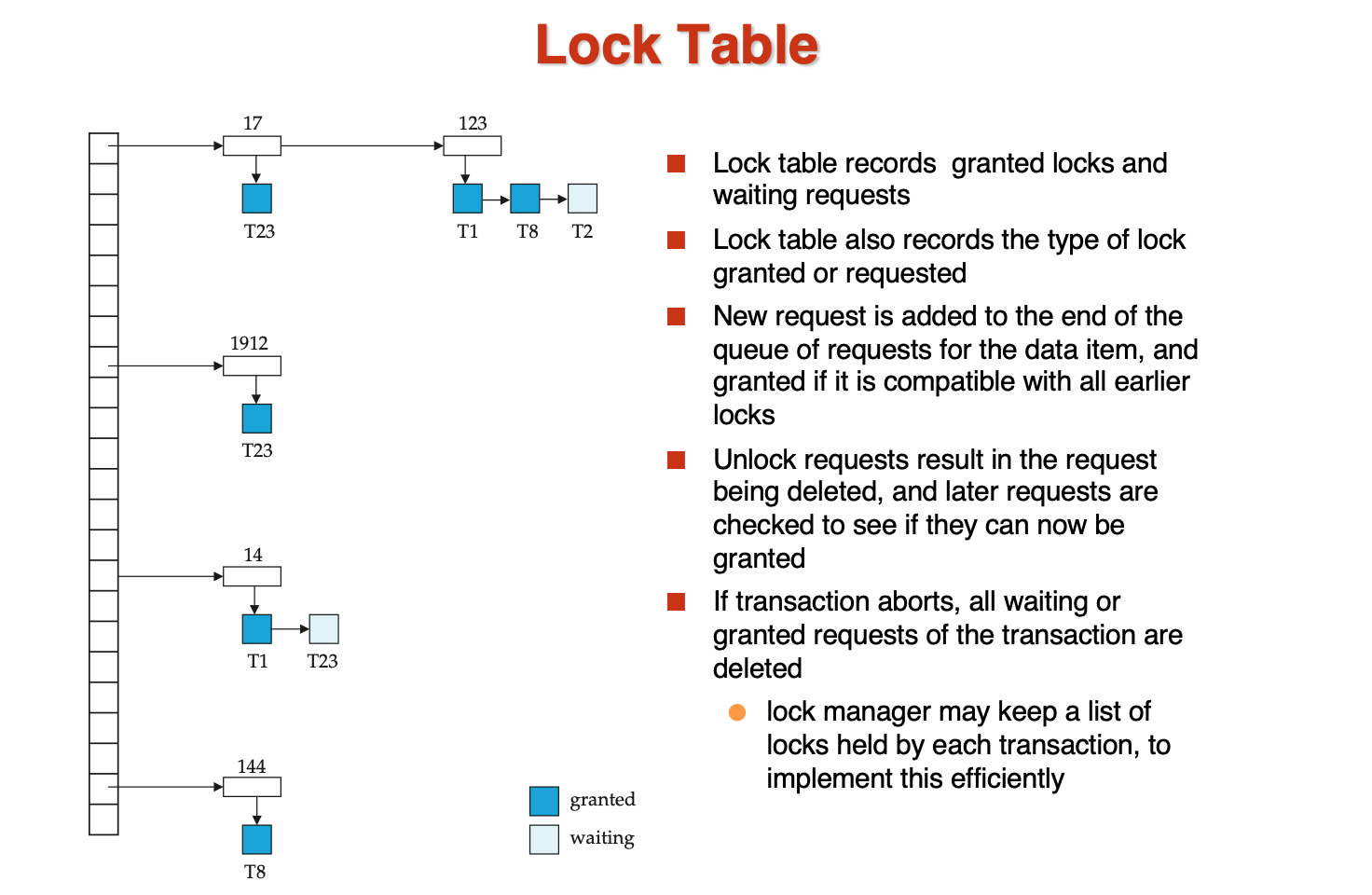
还需要有一个辅助的数据结构来记录每个事务所具有的锁,以及锁的类型
- Deadlock Handling

循环等待
解决:
- 一次性获得所有的锁/偏序数据
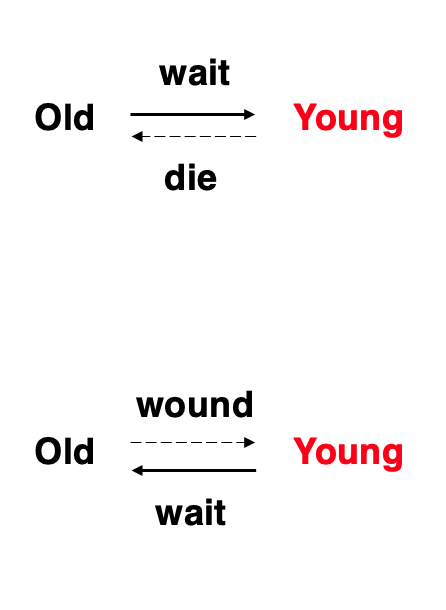
- 抢夺和不抢夺:
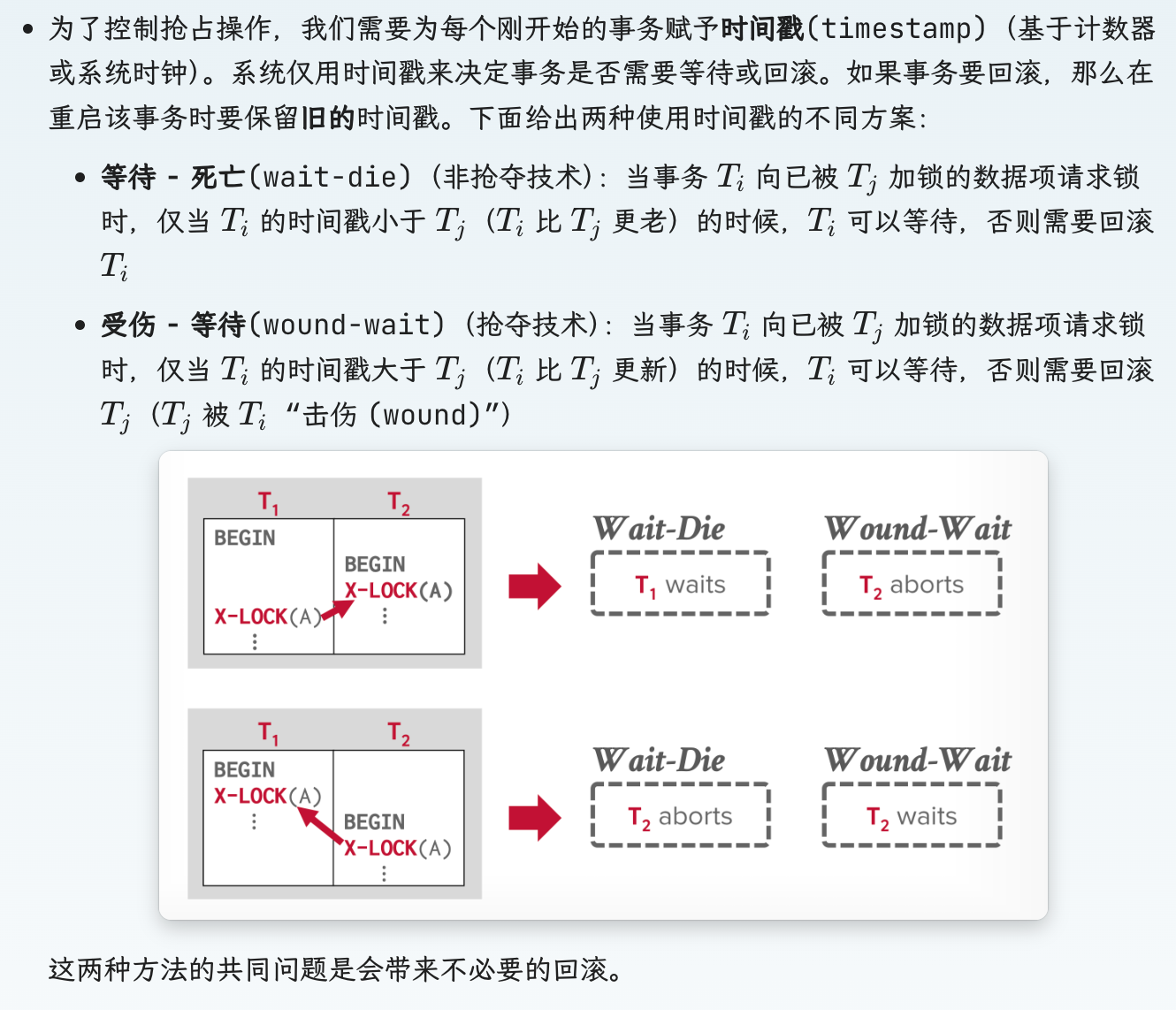
就是两种方式,一种老的等新的(不抢夺),一种新的等老的(抢夺)
- Deadlock Detection
不采用deadlock prevention,而是执行deadlock detection,因为我们有所有的等待信息(lock table)
采用wait-for graph来检测死锁:
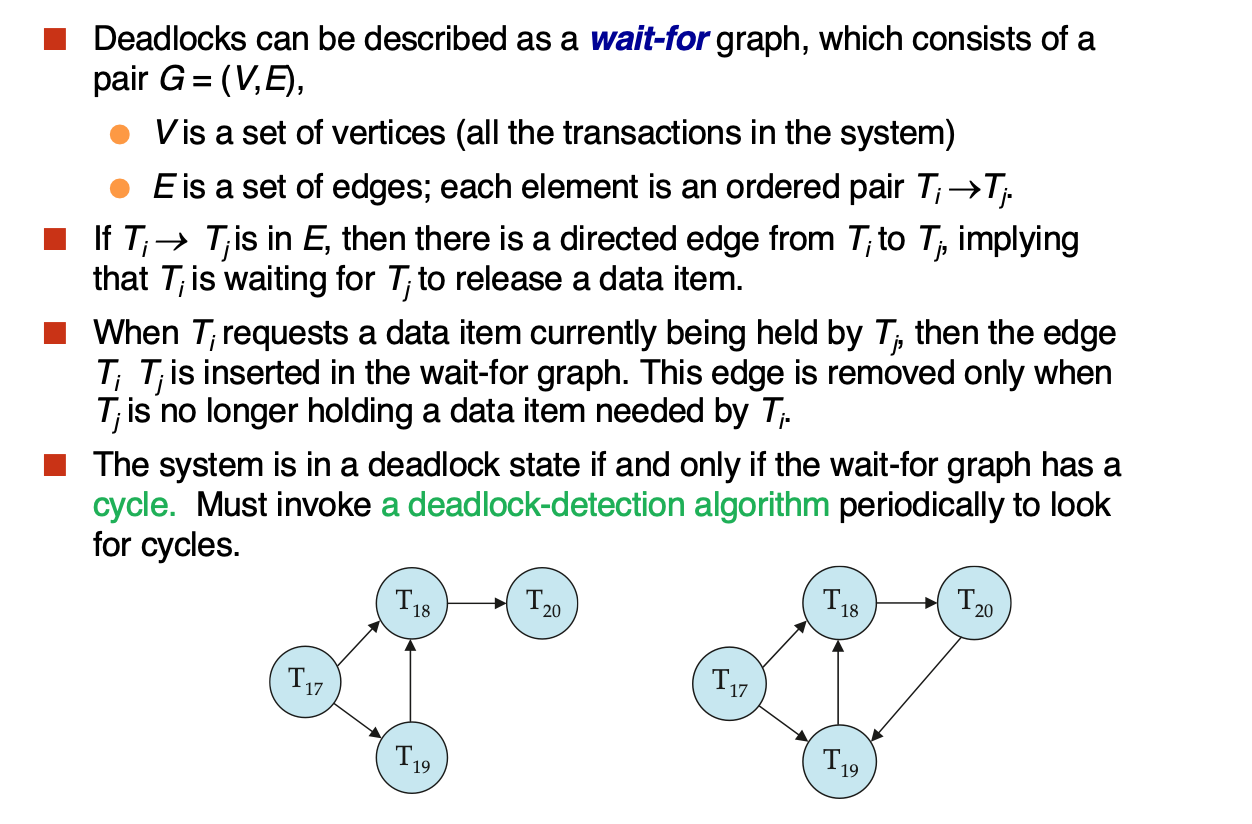
监测到死锁后,需要进行recovery,选择一个或者多个事务进行rollback
有可能出现总是将相同事务作为“受害者”的情况,这样的话该事务就永远没法完成任务,因而存在饥饿问题。所以我们必须确保事务被选为“受害者”的次数不超过指定次数。最常见的解决方案是在成本因子中包含回滚次数。
- Tree-Based Protocol
将数据之间的关系处理成偏序(图),再取消S锁,只允许X锁,这样得到了一个树结构:
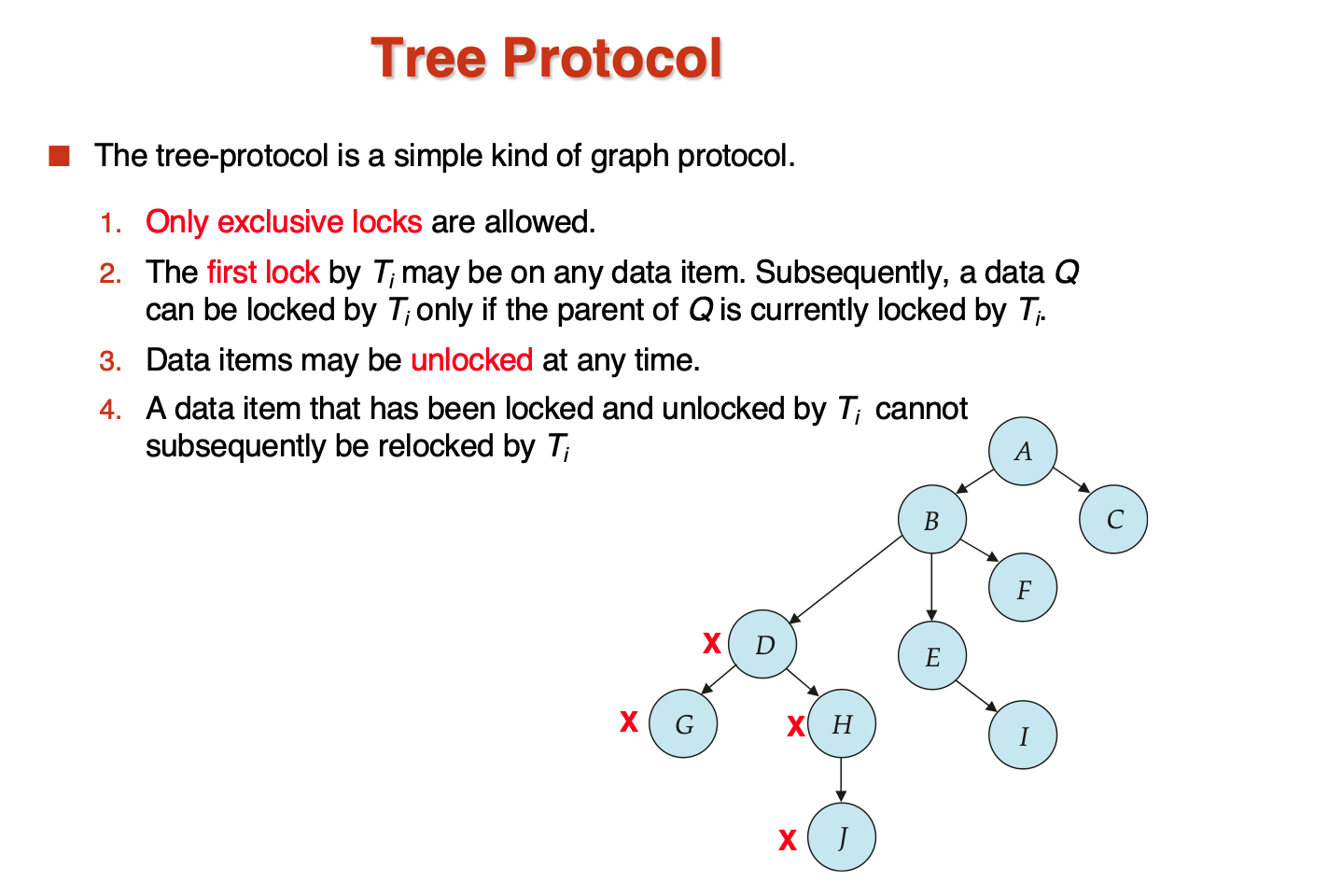
这样的好处是:
- unlock阶段可以比two-phase更早,waiting更少
- 没有死锁
坏处:
- 不保证可恢复,需要增加commit dependency
-
事务可能lock比需要的lock更多(因为树形结构,为了访问两个子节点,必须先访问最近的公共祖先)
-
Granularity
我们需要一种机制,能够让系统定义多个层级的粒度(granularity):也就是说让数据项的大小可变;并定义一种数据粒度层级,其中小粒度会被包含在大粒度里面。这样的层级可以用一棵树表示
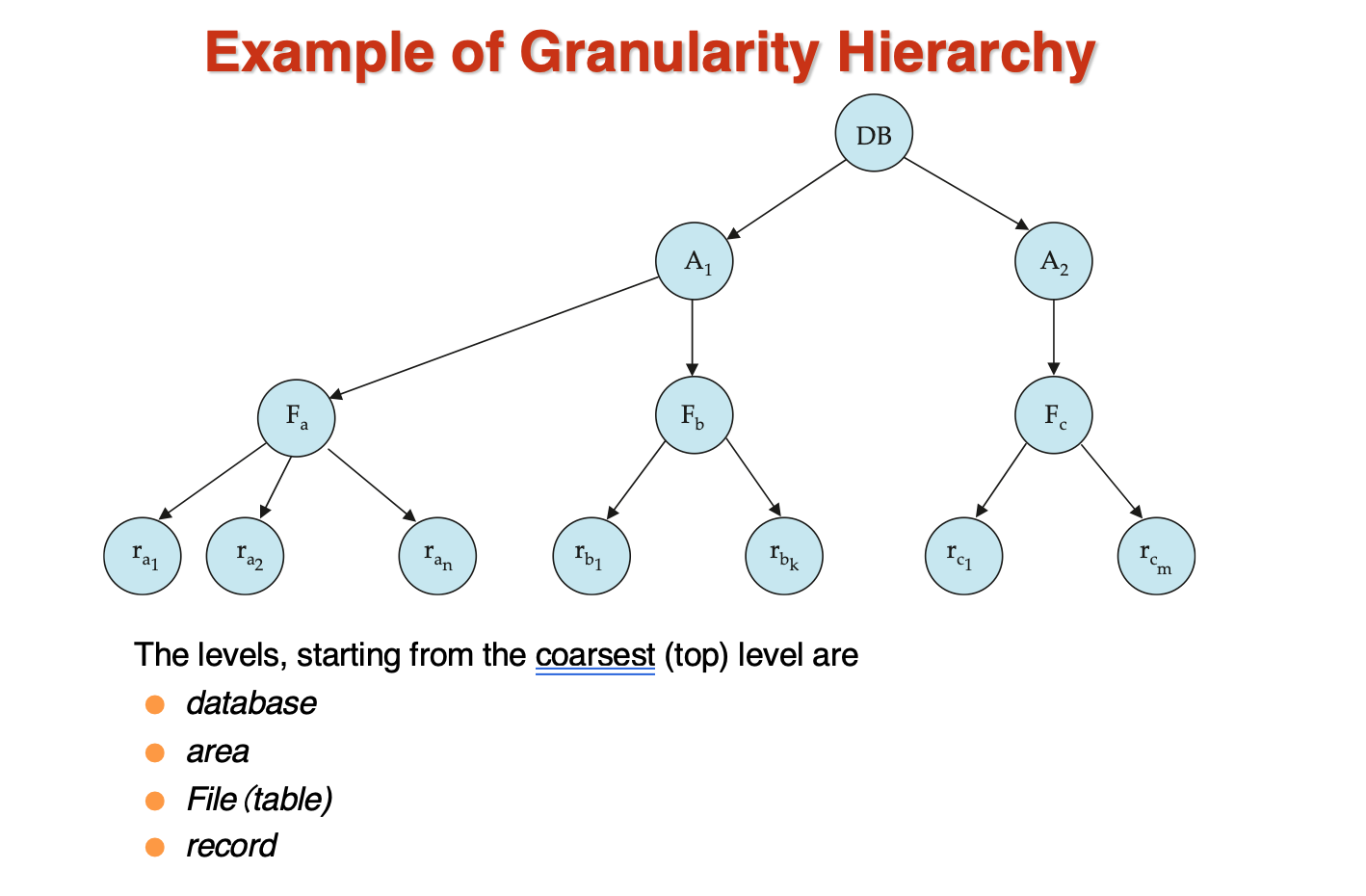
- 每个节点可以被单独加锁,当一个节点被加锁后,他的所有子节点被隐式加锁
-
如果事务要对一个节点加锁,需要遍历所有的祖先节点,如果发现路径上有不兼容的锁,则需要等待
-
Intention Locks

如果解释一下用法的话,intention就是表示一个意向,如果我要对子节点进行S,那么我需要对父节点进行IS,表示意向,同样的,如果我要对子节点进行X,那么我需要对父节点进行IX,表示意向
SIX可以理解为S+IX,表示需要读所有节点,但可能需要在过程中进行写
- 最细粒度的数据只需要S、X锁
- 粗粒度的数据需要IS、IX锁,同时也可以被S、X锁
- 对粗粒度加S、X锁时,下方就不用加锁了,因为已经隐式加锁了,同样的下方有S、X锁时,上方的父节点需要连续的有IX锁
- 加锁过程从上到下,释放锁过程从下到上
- 一个事务的加锁解锁过程是two-phase的,加锁过程中不能解锁
- 会发生死锁
Example
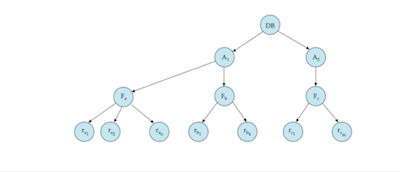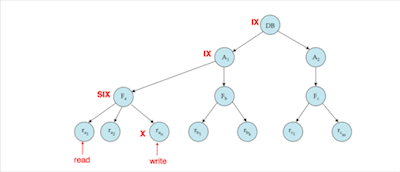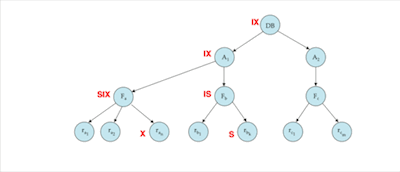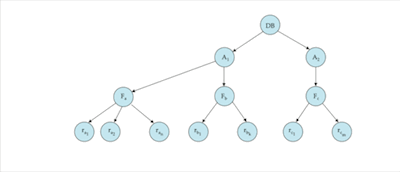
- Insertion and Deletion
Recovery¶
- Idempotent: 幂等性,恢复操作可以重复执行,不会产生副作用
Log-Based Recovery¶
就是先对已经提交的事务进行Redo,再对活跃的事务进行Undo,将数据库恢复到crush的现场
Example

在这个例子中,第12行执行完了正常的程序,之后T2发生了rollback,回滚了他做的write操作,这段会被记录到补偿日志。
然后发生了crush,需要执行整个log一直到最下方,进行重演
这时的可以发现T4是没有abort或者commit的,所以要进行undo,所以有了红线下方的两个操作,他们是在recovery的过程中才出现的
-
先写日志再写数据,这被称为Write-Ahead Logging原则
-
commit 的标志不是完成所有数据的磁盘写,只要是日志中完成了记录commit,并将日志写入磁盘,就可以认为commit完成了,数据的部分即使crush了,也可以redo
-
对于concurrent的transaction,我们保证一个事务对一个数据项的操作是加有排他锁的,这样就不会造成混乱
Checkpoint¶
Example

在进行ckpt的时候需要停止所有的活动,然后将已经写好的log送入磁盘,将数据写入磁盘,记录还没有commit或者abort的事务,存入一个Undo list。
在例子中ckpt的下方,先发生了一起T2的rollback,我们执行掉他以后发生了crush,先进行redo,只需要从ckpt开始,然后进行undo,现在list中只有T4,所以只有T4需要undo。
- 数据库的buffer构成:
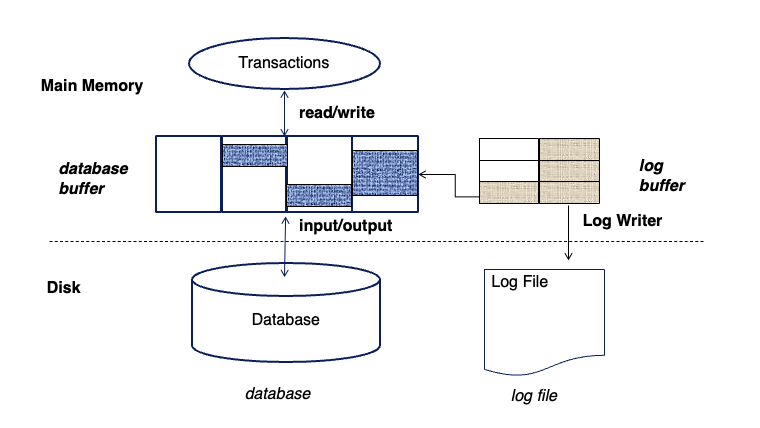
Fuzzy Checkpoint
为了避免ckpt的时候大量的IO导致的阻塞,将ckpt从一个点变成一个过程,流程是:
- 用一个last-ckpt来指向最后一个已经完全完成的ckpt
- 短暂停一下,写一个checkpoint
- 首先标记buffer中的M个脏页,然后逐渐将他们写入磁盘,当写完M个脏页后,将last-ckpt更新为当前的ckpt
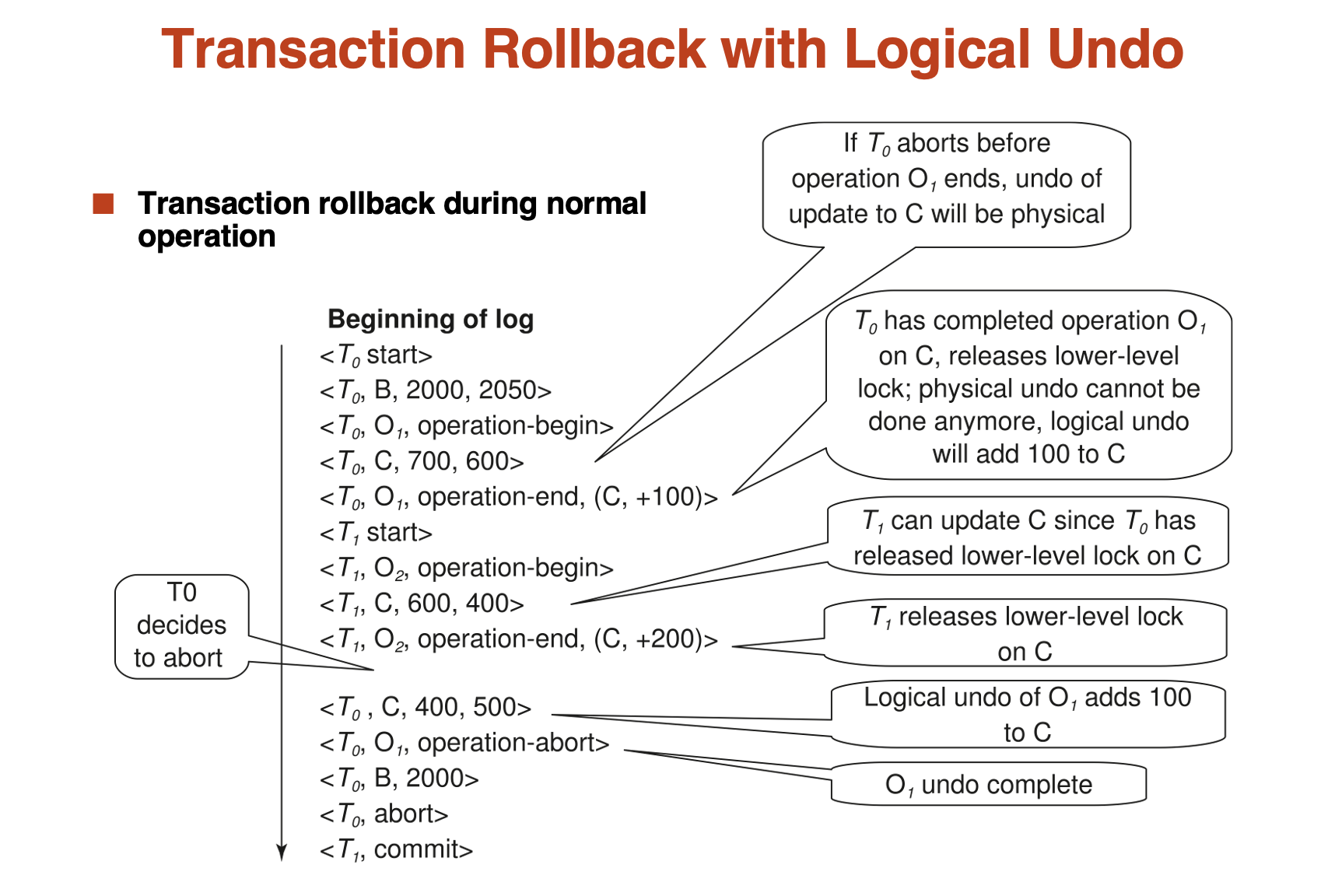
Early Lock Release and Logical Undo¶
Logical Undo 就是记录一个operation log条目,表示一个事务对一个数据项的操作,与原始的physical undo直接将数据改为old值不同,记录下操作后我们的undo就变成了对当前数据的逆操作,即使当前数据变化了,也没关系。
Example
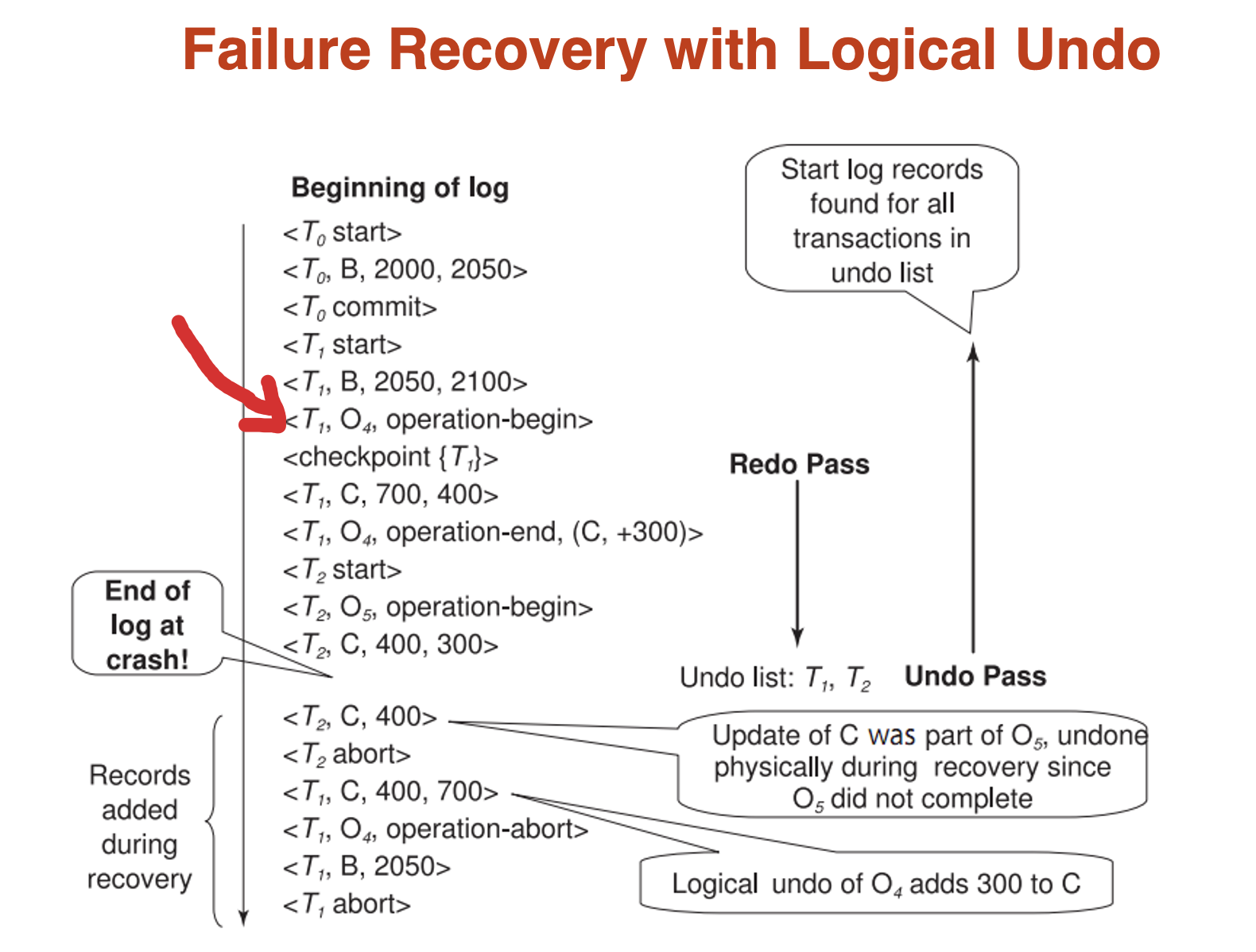
这里我们就可以发现,如果crush发生在operation记录中,说明operation记录不完全,我们就只能进行physical undo,如果是已经记录完全的,我们就可以利用undo info U 进行logical undo,并在结束时写operation-abort
同时注意如果是logical rollback,大体上与recovery是相似的,就是通过有没有完成operation-end来看:
- 如果已经完成operation-end,那么我们就可以进行logical undo,然后加入operation-abort
- 如果还没有完成operation-end,我们只能舍弃掉下一个operation之前的所有语句
Example
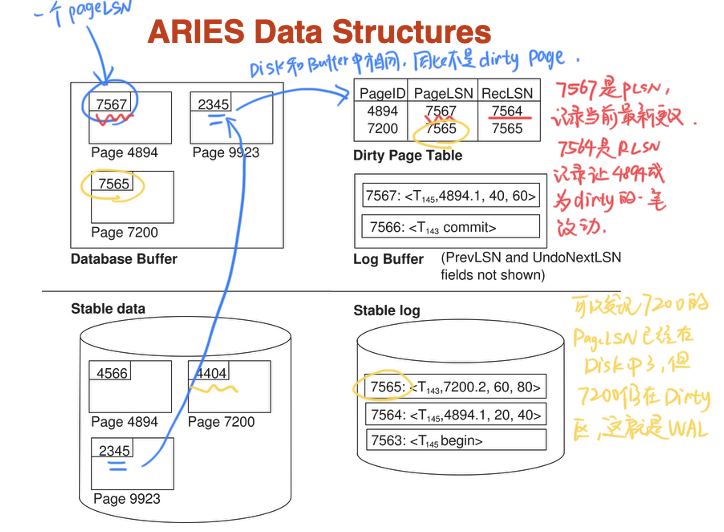
ARIES¶
-
LSN:
每个log entry都有一个LSN,表示这个log entry在log中的位置,由于有很多log file共同组成log,所以每个log entry就是文件号+偏移量
-
Dirty Page Table:
记录了buffer中被修改过的页,对应的PageLSN、RecLSN
- PageLSN:
每个Page都有一个PageLSN,用于记录更新过这个Page的最后一个LSN,这样当redo的时候,任何小于这个LSN的日志记录都可以被忽略(这个对于幂等性十分重要,因为非物理的redo再次执行会导致数据不一致)
-
RecLSN:
这个LSN之前的所有LSN已经被作用到磁盘中,这条LSN记录的是让这个Page成为dirty的第一个LSN,这也是恢复的起点
- Analysis Phase
分析阶段,目的是搞清楚再崩溃瞬间数据库的状态
- 从stable log中最近的ckpt开始顺序读到日志文件末尾
- 收集信息,建立两张表:
- 事务表:记录crush时的活跃事务
- 当扫描到一条begin transaction时,将事务加入事务表,当扫描到commit或者abort时,将事务从事务表中移除,结束时得到的就是失败者事务
- 脏页表Dirty Page Table:记录所有可能在崩溃时比disk中更新的数据
- 当扫描到一个针对不在DPT的页的写操作时,将该页加入DPT,同时这条日志的LSN就是RecLSN
- 事务表:记录crush时的活跃事务
这一阶段得到的就是一个失败者事务表、脏页表、以及一个RedoLSN(min from all RecLSN,如果没有dirty page,那么就是ckpt的LSN)
- Redo Phase
重复历史,将数据库恢复到crush的瞬间状态,确保所有已写入日志的修改(无论来自已提交的事务还是未完成的事务)都真实地反映在数据页上。
- 从RedoLSN开始,顺序读取日志文件到末尾
-
重做:对于扫描的每个日志,如果:
- 判断一:这个页不在脏页表中,或者,这个这个日志的LSN < 他在脏页表中的RecLSN,就跳过它不用重做
- 判断二:否则,将页从disk中取出,如果这个页在disk中的PageLSN < 这个日志的LSN,那么就重做该日志
-
重做后,更新PageLSN
这一阶段会恢复到与crush前完全一致的状态,即使是失败者也会被重做
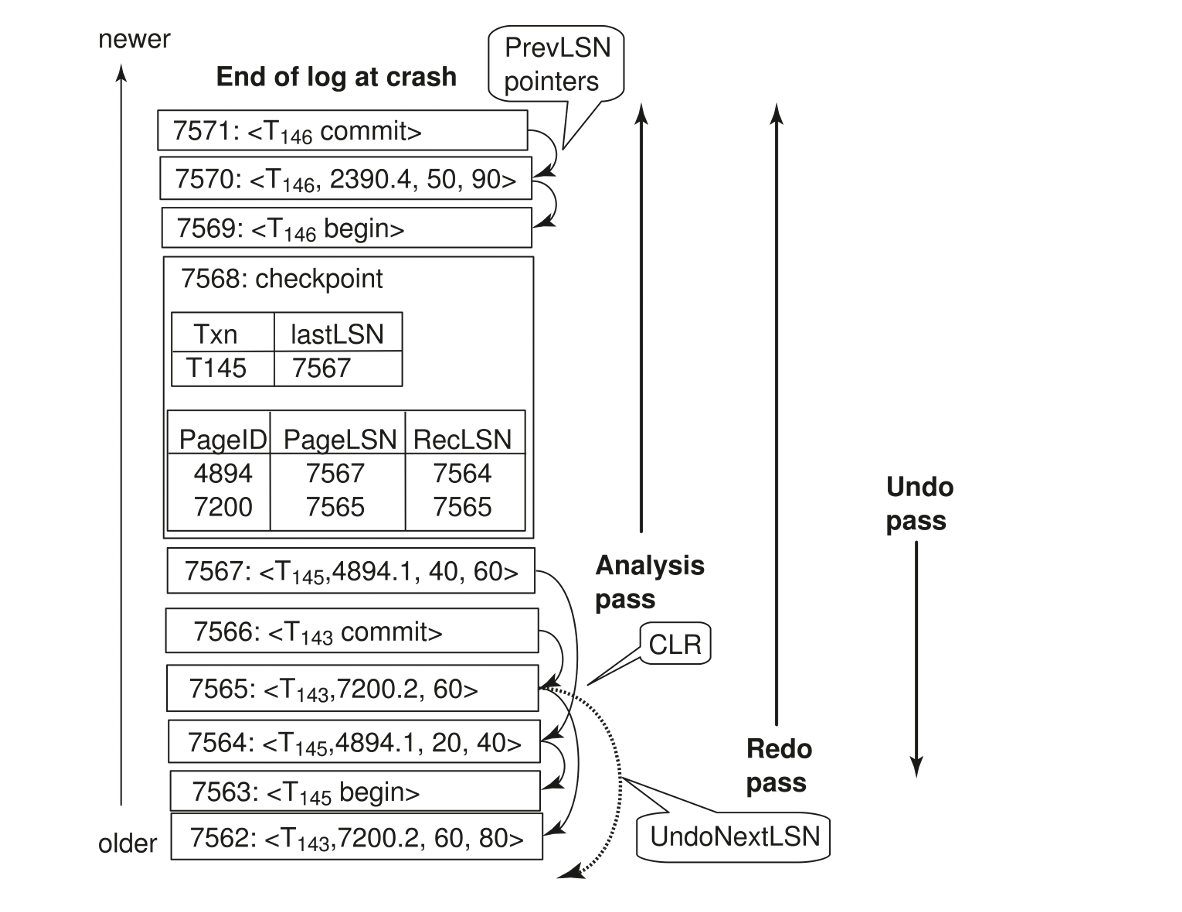
- Undo Phase
目标是清理现场,回滚失败者的修改,保证原子性
- 在失败者事务中,从最后一条开始,反向扫描。对于每一个事务,通过PrevLSN找到关于这个事物的所有日志
- 按顺序将这些日志的操作逆向执行
- 每执行一次逆向,生成一个补偿日志记录CLR,记录下逆向操作
- 当一条失败者事务的所有操作都被逆向执行完成,为他写一个end日志
这个阶段中CLR是为了防止在undo的过程中再次crush,这样恢复时不用重做已经补偿过的操作,保证幂等性
这个阶段结束后,数据库恢复到所有已提交事务都生效,所有未提交事务都回滚
- 一个undo phase的优化:
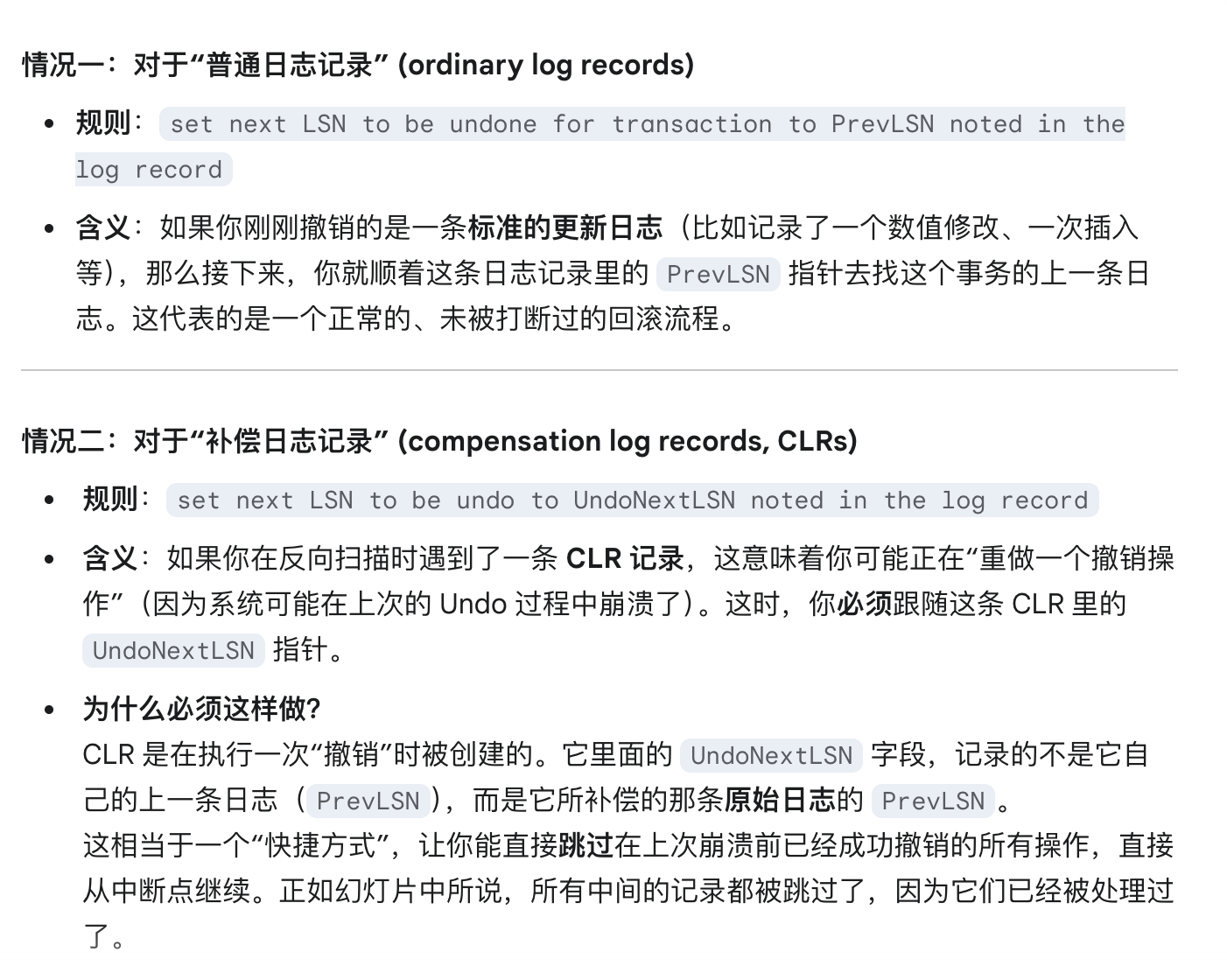
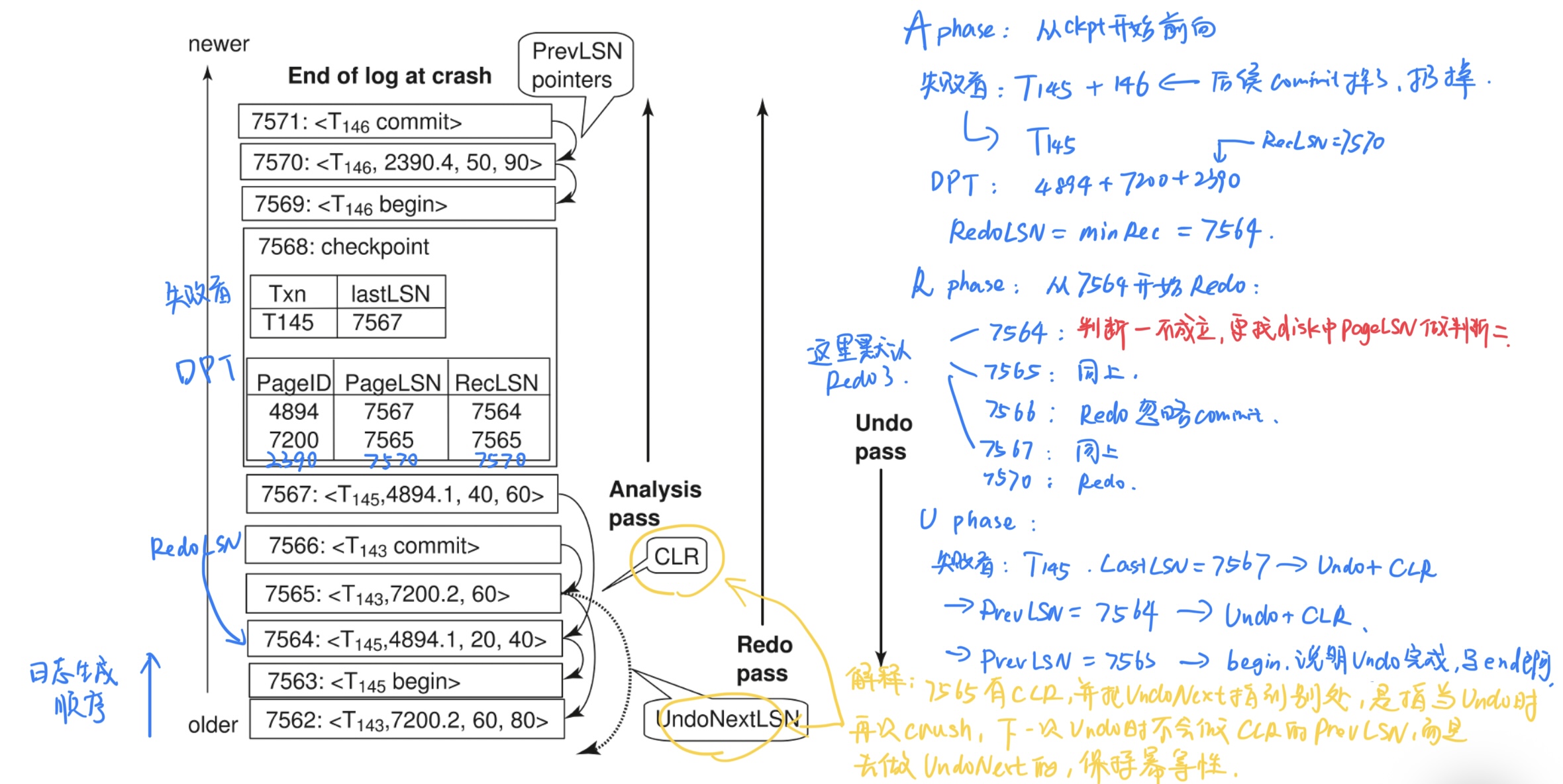
上课时老师讲的undo phase与这里的不太相同,是一个更优化方案,rather than undo 每个事务的所有操作,我们选择找到待undo 的LSN集合,选取其中LSN最大的日志进行undo,然后根据这个日志的PrevLSN(或UndoNextLSN)找到下一个待undo的LSN,重复这个过程,直到全部undo完成
关于这里选择PrevLSN还是UndoNextLSN:
Example
留言