跳转至

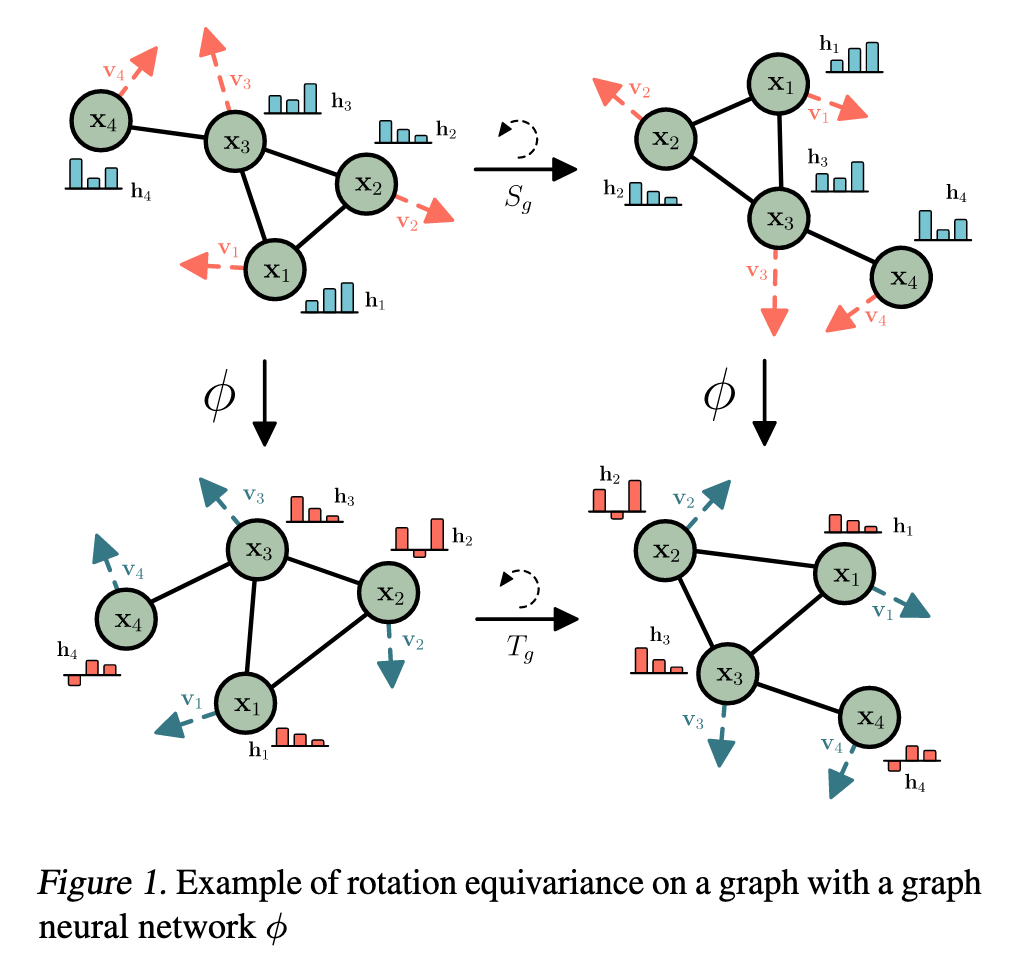
Equivariant

Equivariant 等变性是物理中的一个关键性质，在物理中，等变性是指物理定律在某种变换下保持不变。例如，牛顿第二定律在平移变换下保持不变，这就是等变性。在物理中，等变性是物理定律的数学表达，是物理定律的数学基础。

Mathematical Definition

令\(G\)是一个抽象群，\(g \in G\)，我们说一个变换函数（或神经网络层）\(\phi: X \to Y\)是\(g\)等变的，如果：

对于一个在\(X\)上定义的变换函数\(T_g: X \to X\)对应存在一个在输出空间\(Y\)上的等价变换函数\(S_g: Y \to Y\)，使得：

\[ \phi(T_g(x)) = S_g(\phi(x)) \]

这里讨论三种等变性：

  • Translation 平移等变性：将输入平移会导致输出产生相对应的平移。

    \[ \mathbf{y} + \mathcal{g} = \phi(\mathbf{x} + \mathcal{g}) \]

  • Rotation 旋转等变性：将输入旋转会导致输出产生相对应的旋转。

    对于任何正交矩阵\(Q\)，令 \(Qx=(Qx_1, \dots, Qx_n)\)，那么：

    \[ Qy = \phi(Qx) \]

  • Permutation 置换等变性：

    \[ P(y) = \phi(P(x)) \]

    其中\(P\)是行索引上的置换

    GNN是置换等变的。

首先了解一下什么是EGNN，EGNN相当于是零件，用于构建一个等变的图理解器，而EDM则是用这个零件组装出一个强大的分子生成机器。

EGNN

Abstract

GNN在处理图数据时具有很强的表达能力，但是GNN的问题在于只关心拓扑关系（节点之间的连接），而忽略了节点的几何信息（节点的位置）。如果我们要设计一个既能注意拓扑也能注意几何信息的网络，那么他必须具备等变性。

Summary

EGNN通过引入GNN节点中所不具有的节点位置\(x_i\)，并将其纳入图卷积层的更新方式来使得GNN具有等变性。

我们来看一下具体的实现方法：

Note

这里放一下同一notation下两种更新算法

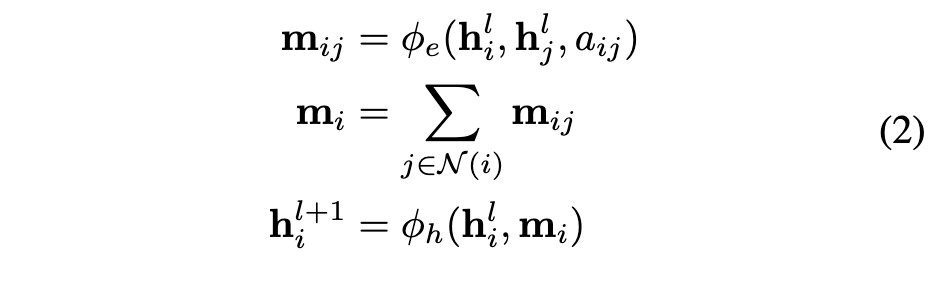
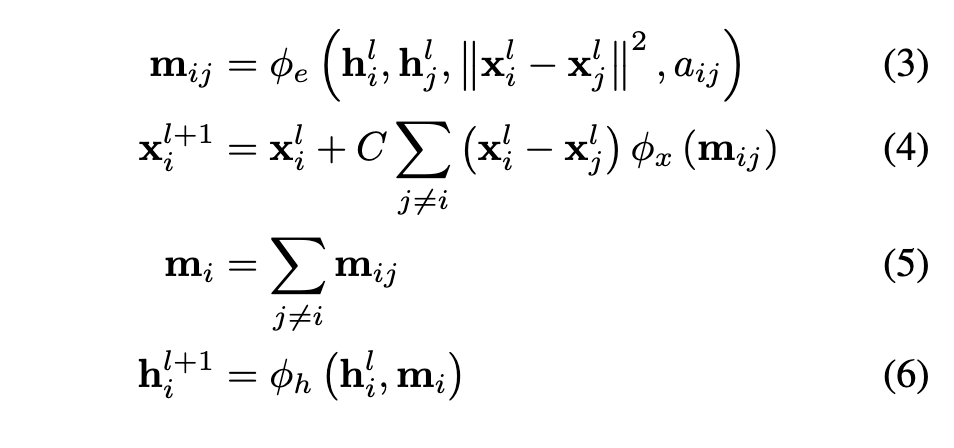
主要区别就是在对于消息传递的更新上，以及补充了一下我们加入的位置坐标的更新方式

  • (3)

    在边操作\(\phi_e\)中，我们加入了节点之间位置距离的平方项\(||x_i-x_j||^2\)，而距离的平方是一个标量，对于旋转和位移是不变的（invariant）。其余的信息与GNN一致都是标量，所以输出的消息也是不变的。

  • (4)

    对于位置的更新十分重要。在这个公式中，每个粒子的位置是通过所有相对差值的加权和来更新的，这个权重由位置操作函数\(\phi_x: \mathbb{R}^d \to \mathbb{R}^1\)来计算，输入得到的消息信息，输出一个标量值。C被选为\(\frac{1}{M-1}\)。而其中的向量差的合，因为是等变向量，所以整个式子是等变✖️不变，依然是等变的。

EDM

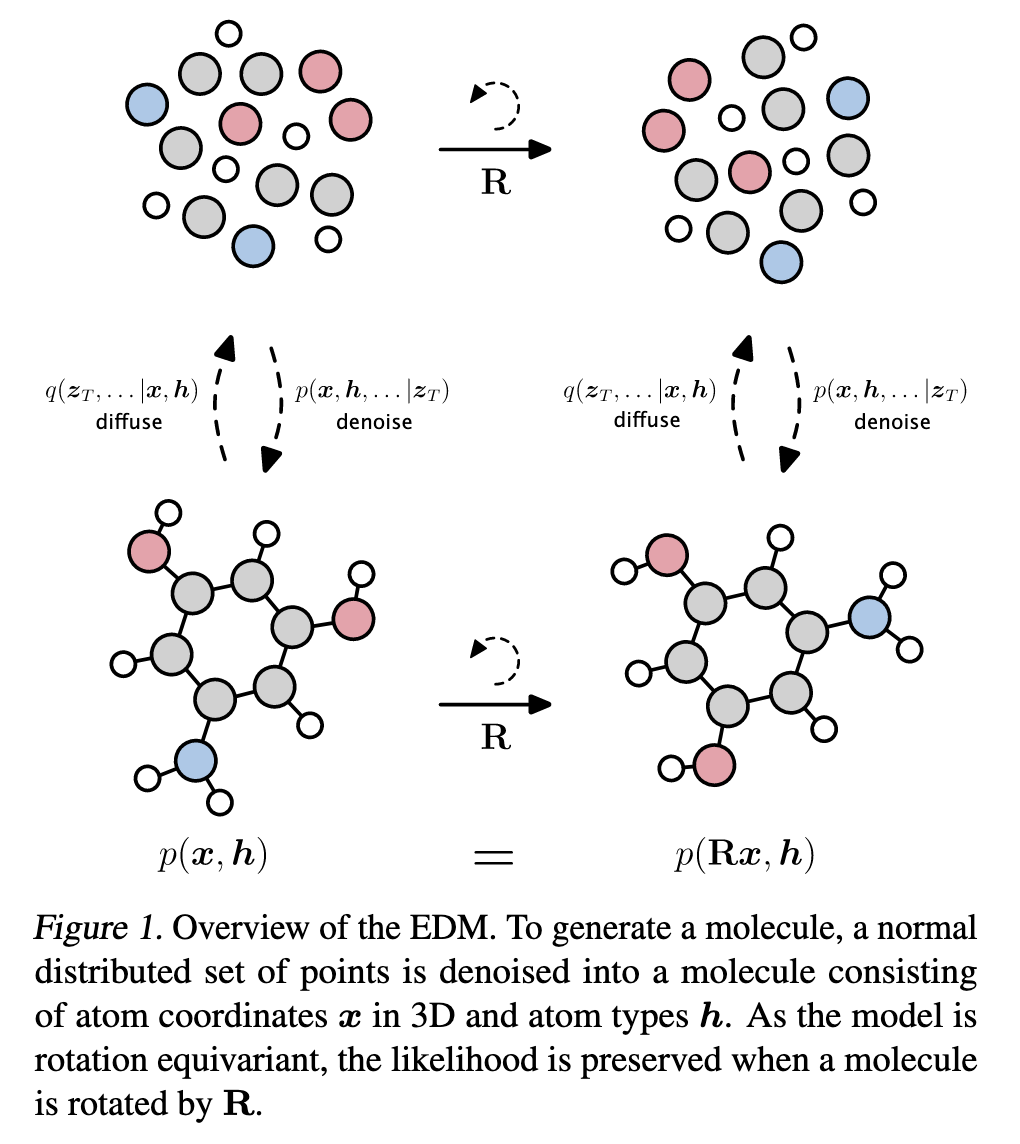
Abstract

扩散模型在图像上可以取的巨大成功，离不开图像的数据结构本质——grid上的连续值（像素）。而分子本身是无序的点云（unordered point cloud），每个点（atom）包含两个信息：连续坐标和离散元素类别，同时图像往往只要求平移不变性，而分子必须要求有E(3)对称性，即生成过程和结果不能因为你旋转或平移了坐标系而改变。

这时我们的任务就不仅仅是还原噪声，更应该知道每个零件是什么，应该放在哪儿，并且构筑过程中不能因为观察者更换视角而改变。

Summary

完全针对分子设计定制的扩散模型，结合了位置连续信息\(x\)和离散元素类别\(h\)，使用EGNN作为神经网络\(\epsilon_\theta\)，保证了等变性。

在对Diffusion模型的等变性进行分析时，首先要知道我们的等变性主体对象是概率分布：

Equivariance of Probability Distributions

一个条件概率分布是等变的，如果：

\[ p(y|x) = p(\mathbf{R}y|\mathbf{R}x) \quad \forall \text{ orthogonal } \mathbf{R} \]

一个概率分布是不变的，如果：

\[ p(y) = p(\mathbf{R}y) \quad \forall \text{ orthogonal } \mathbf{R} \]

然后我们需要知道为什么概率分布在经过EGNN \(\epsilon_\theta\) 处理后，会满足等变性：

这部分文章用了简短的一个段落来阐述

我们分三步解释这个原理：

1. 单步变换：一个等变的可逆的函数作用在一个不变的分布上时，这个分布不变。

2. 多步马尔可夫链：在等变转移概率中，状态转移的规则是等变的。

3. 应用到Diffusion：Diffusion起点的纯噪声\(p(z_T)\)是高斯分布，是一个不变分布，反向去噪的过程如果使用等变的神经网络，那么转移概率也是等变的，最终得到的分子分布也就是等变的。

Value

这段证明的价值在于：

  • 保证正确性：不变初始分布以及等变转移过程保证了最终的分子分布是等变的。
  • 避免学习坐标系偏见：模型学会的是分子的内在结构规律，而不是它们在空间中的偶然朝向。
  • 泛化能力和效率：模型本身就是等变的，就不需要花费参数学习物理常识

Details of Model

Section 3

Points and Features

在E(3)中我们考虑point clouds \(\mathbf{x} = (x_1, \dots, x_M) \in \mathbb{R}^{M \times 3}\)，且带有对应特征\(\mathbf{h} = (h_1, \dots, h_M) \in \mathbb{R}^{M \times nf}\)，nf是特征的维度。

特征对于group transformation是不变的，但是坐标对于旋转、反射、平移是等变的。

在得到数据的表示方式后，我们对于这里使用的EGNN进行定义：

EGNN in EDM

在这里我们考虑所有原子之间的相互作用，因此假设一个全连接的图，每个节点\(v_i\)有对应的位置\(\mathbf{x}_i\)和特征\(\mathbf{h}_i\)。\(\mathbf{x^{l+1}}, \mathbf{h^{l+1}} = \text{EGCL}(\mathbf{x^l}, \mathbf{h^l})\) 定义如下：

\[\mathbf{m}_{ij}=\phi_e\left(\mathbf{h}_i^l,\mathbf{h}_j^l,d_{ij}^2,a_{ij}\right),\mathbf{h}_i^{l+1}=\phi_h(\mathbf{h}_i^l,\sum_{j\neq i}\widetilde{e}_{ij}\mathbf{m}_{ij})\]
\[\mathbf{x}_i^{l+1}=\mathbf{x}_i^l+\sum_{j\neq i}\frac{\mathbf{x}_i^l-\mathbf{x}_j^l}{d_{ij}+1}\phi_x\left(\mathbf{h}_i^l,\mathbf{h}_j^l,d_{ij}^2,a_{ij}\right)\]
  • \(\widetilde{e}_{ij} = \phi_{inf}(m_{ij})\)是对边的注意力软估计
  • 所有的可学习参数在\(\phi_e, \phi_h, \phi_x, \phi_{inf}\)中
  • Diffusion Process

将\([·,·]\)定义为concatenation操作，我们定义等变noising process为在潜变量\(\mathbf{z_t} = [\mathbf{z_t^{(x)}}, \mathbf{z_t^{(h)}}]\)上：

\[\begin{aligned} q(\mathbf{z}_t|\mathbf{x},\mathbf{h})&=\mathcal{N}_{xh}(\mathbf{z}_t|\alpha_t[\mathbf{x},\mathbf{h}],\sigma_t^2\mathbf{I})\\ &= \mathcal{N}_x(\mathbf{z}_t^{(x)}|\alpha_t\mathbf{x},\sigma_t^2\mathbf{I})\cdot\mathcal{N}(\mathbf{z}_t^{(h)}|\alpha_t\mathbf{h},\sigma_t^2\mathbf{I}) \end{aligned}\]

center of gravity

在原文中提到这样一段话：

他提到我们的分子生成并非是可以在空间中随意移动的，因为如果想要保证平移不变，我们需要将概率分布在无限大的空间中平铺，这显然是不可能的。

所以我们采取的做法是不考虑平移，将质心直接放在(0,0,0)进行建模，方法是施加约束

\[\sum_{i=1}^M x_i = 0\]

此时我们不再关注分子的绝对位置，只需要考虑原子之间的相对位置

  • Denoising Process

还是按照传统Diffusion的流程定义去噪过程，定义优化目标：

\[\mathcal{L}_t=\mathbb{E}_{\mathbf{\epsilon}_t\mathbf{\sim}\mathcal{N}_{xh}(0,\mathbf{I})}\left[\frac{1}{2}w(t)||\mathbf{\epsilon}_t\mathbf{-}\hat{\mathbf{\epsilon}}_t||^2\right]\]

Dynamics

Section 3.2

\[\hat{\mathbf{\epsilon}}_t^{(x)},\hat{\mathbf{\epsilon}}_t^{(h)}=\mathrm{EGNN}(\mathbf{z}_t^{(x)},[\mathbf{z}_t^{(h)},t/T])-[\mathbf{z}_t^{(x)},\mathbf{0}]\]

这个公式给出了噪声的更新方式：

  • 对特征信息，由于其具有不变性，可以加入时间信息\(t/T\)来调整不同步数的更新方式
  • 位置信息的更新是一个残差更新，EGNN输出的结果减去后方的初始值得到的才是噪声

Zeroth Likelihood Term

Section 3.3

经过denoising后，我们得到的就是最终的连续状态\(\mathbf{z}_0 = [\mathbf{z}_0^{(x)}, \mathbf{z}_0^{(h)}]\)

但是分子是由离散的原子类型+整数电荷+连续坐标组成的，现在我们分别讨论他们如何得到

  • 电荷

直接采用四舍五入的方式进行估算

\[p(\mathbf{h}|\mathbf{z}_0^{(h)})=\int_{\mathbf{h}-\frac{1}{2}}^{\mathbf{h}+\frac{1}{2}}\mathcal{N}(\mathbf{u}|\mathbf{z}_0^{(h)},\sigma_0)\mathrm{d}\mathbf{u}\]

因为去噪最后一步的噪声的值非常小，或者说加噪过程的第一步噪声非常小，所以我们认为在这一步的后验概率\(q(\mathbf{h}|\mathbf{z}_0^{(h)})\)会无限接近1，这就告诉我们模型的输出值\(\mathbf{z}_0^{(h)}\)已经非常接近真实值\(\mathbf{h}\)，所以我们可以直接采用四舍五入的方式找到他最接近的那个h

  • 原子类型

在刚才电荷问题的讨论中，我们会想0.5是一个介于0和1之间的数值，如果元素也是按照这个思路，那我们很可能会让模型觉得N是一个介于C和O的中间体，这种bias是没有道理的，所以我们用独热编码来处理这种离散的数据类型，然后在这个categorical distribution中选择最大值

\[p(\mathbf{h}|\mathbf{z}_0^{(h)})=\mathcal{C}(\mathbf{h}|\mathbf{p}),\mathbf{p}\propto\int_{\mathbf{1}-\frac{1}{2}}^{\mathbf{1}+\frac{1}{2}}\mathcal{N}(\mathbf{u}|\mathbf{z}_0^{(h)},\sigma_0)\mathrm{d}\mathbf{u}\]
  • 坐标

对于连续的坐标，我们的处理方式如下：

从最原始的公式出发，我们有\(\mathbf{z}_0^{(x)} = \alpha_0\mathbf{x}_0 + \sigma_0\epsilon^(x)\)，这样其实已经可以反解出来一个真实的坐标，但由于我们不知道确切的噪声项\(\epsilon^(x)\)，所以x的最佳估计值就是概率中心\(\mathbf{z}_0^{(x)}/\alpha_0\)，也就是文中的公式：

\[q(\mathbf{x}|\mathbf{z}_0^{(x)})=\frac{q(\mathbf{z}_0^{(x)}|\mathbf{x})p_{data}(\mathbf{x})}{\int_\mathbf{x}q(\mathbf{z}_0^{(x)}|\mathbf{x})p_{data}(\mathbf{x})}\approx\frac{q(\mathbf{z}_0^{(x)}|\mathbf{x})}{\int_\mathbf{x}q(\mathbf{z}_0^{(x)}|\mathbf{x})}=\mathcal{N}(\mathbf{x}|\mathbf{z}_0^{(x)}/\alpha_0,\sigma_0^2/\alpha_0^2)\]

但是empirically，作者发现了一个更好的方法，在最后一步再多预测一次噪声\(\epsilon_0^{(x)}\)，用这个噪声作为原始结果的修正项进行微调：

\[p(\mathbf{x}|\mathbf{z}_0)=\mathcal{N}\left(\mathbf{x}|\mathbf{z}_0^{(x)}/\alpha_0-\sigma_0/\alpha_0\hat{\mathbf{\epsilon}}_0,\sigma_0^2/\alpha_0^2\mathbf{I}\right)\]

这样做的另一个好处是可以统一了t=0时的优化目标

留言

欢迎在下方交流~