Skip to content

Backtracking

Intro

解决问题可以将所有可能解罗列出来，但是这样时间复杂度太高，因此需要使用回溯法进行优化

回溯法就是在所有解的空间中进行正确解搜索的一种方式，他通过消除不必要解的搜索空间（剪枝prune）来减少时间复杂度

Example

8 Queens

8 Queens

在一个8x8的棋盘上，放置8个皇后，使得他们互相之间无法进行攻击

对这个问题进行数学化描述：

  • 令\(Q_i\)表示第\(i\)行的皇后，\(x_i\)表示\(Q_i\)的列坐标，\(S_i\)表示\(x_i\)可取值的集合
  • 限制条件：
    • \(S_i = \{1, 2, 3, 4, 5, 6, 7, 8\}\), 表明可能的取值空间大小是\(8^8\)
    • 任意两个皇后\(Q_i\)和\(Q_j\)不能在同一列，即\(x_i \neq x_j\)
    • 任意两个皇后\(Q_i\)和\(Q_j\)不能在同一对角线，即\(|x_i - x_j| \neq |i - j|\)

解决方案：

构建game tree，以四皇后为例：

bk-1

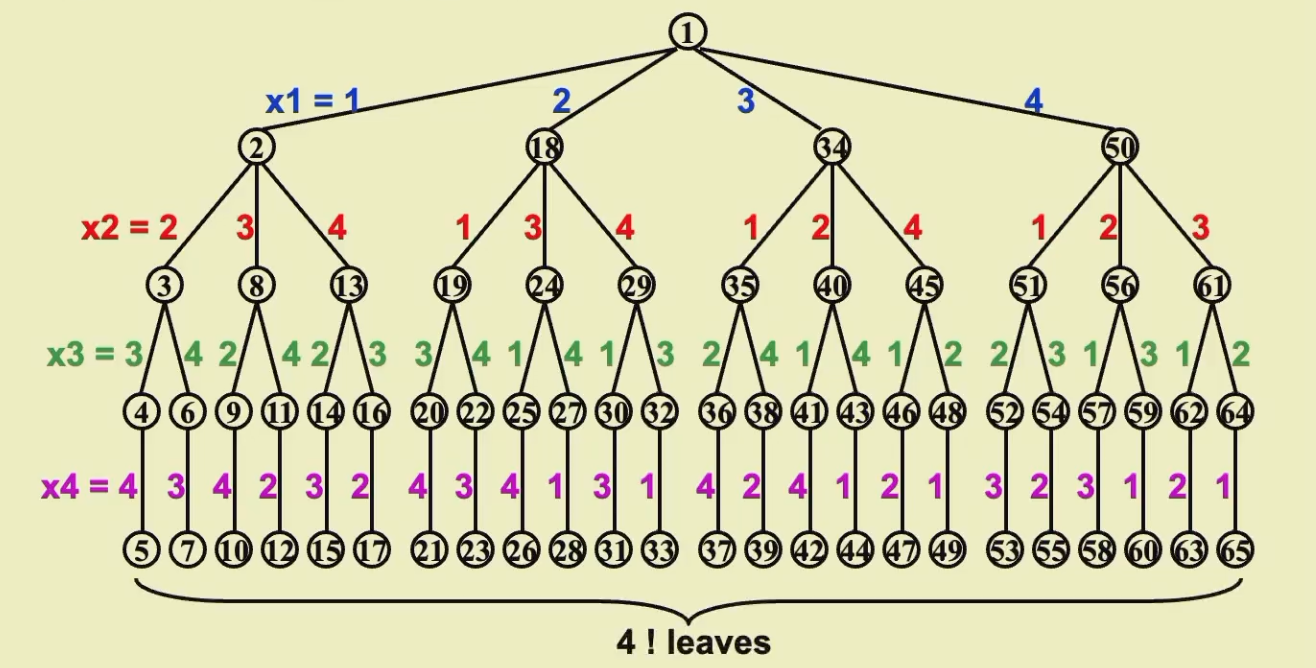
进行深度优先搜索（后序遍历 也就是左中右），在进行遍历的时候主要进行的是对角线的检查（因为本身列的检查在树的结构上已经隐含了）

  • 剪枝的过程就是在我遇到一个节点的时候判断这个节点是否满足条件，如果不满足，就将这个节点以及他的所有子节点都剪掉（不进行遍历）然后对这个节点的兄弟节点进行尝试，如果所有兄弟节点都不满足条件，就说明父亲节点也不满足条件，继续往上返回直到找到一组完整解

Note

实际上树的构建只是为了方便理解，实际上在回溯的过程中，我们并不需要构建树，构建树的过程让我们对“剪枝”这个过程有了更直观的理解，就是在约束条件下提前排除不可能的解，从而减少搜索空间

Hunting On Mars

这里补充一个例题加深对树的构建的理解

问题是：在火星上有一个图，图中的每个节点有可能有兔子(1)也有可能没有兔子(0)，但是猎人出发时所背的氧气只能支撑他走\(k\)步并且需要返回出发点，并且猎人至少需要抓到\(m\)只兔子，找到这样的路径

在这里有两个约束条件：

  • 猎人只能走\(k\)步并且需要返回出发点
  • 猎人需要抓到\(m\)只兔子

这里我们构建树的思路是以路过的节点数作为树的节点，以猎人走过的路径作为树的边，同时计算猎人走过的路径上的兔子数量

剪枝的条件是：

  • 如果当前节点走完剩下的步数小于所需的兔子数量，那么就剪枝
  • 当前节点距离出发点的最短路长度大于剩余的步数，那么就剪枝

但是这里比较tricky的地方在于我们如何进行遍历，如果采用广度优先搜索，那么我们大概率会遍历所有可能的路径，这样时间复杂度会非常高，因此我们采用深度优先搜索，这样在求到一组解之后就可以进行返回，从而节省了时间

Key of pruning

  • 由这个例子我们可以看到在进行剪枝条件的设计时，我们可以考虑放弃一个条件而严格遵循另一个条件
  • 高效的剪枝往往不是依据当前所处节点的，而是具有预见性的剪枝

The Turnpike Problem

The Turnpike Problem

在一条直线上有多个点，这些点之间的距离是\(d_1, d_2, \cdots, d_{n}\)，共\(\frac{n(n-1)}{2}\)个距离，现在要找到这些点在直线上的位置，已知最左边的第一个加油站的位置是固定的在\(0\)

  • 分析

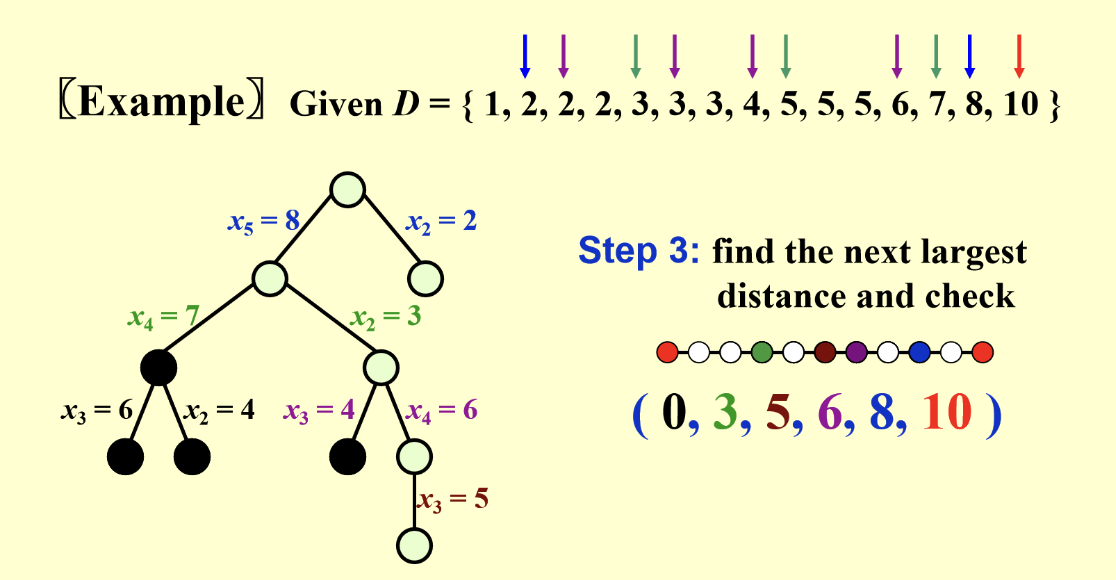
    最大的距离一定是最左边的点\(0\)和最右边的点\(d_n\)，接着处理第二大的距离，但这时最左边的点可以和右边的第二个点构成这个距离，最右边的点也可以和左边的倒数第二个点构成这个距离，所以这就引入了这个问题的game tree

    就是选取左边还是右边，然后通过检查这个新加入的节点与其他已存在节点构成的距离是否在原距离集合中，在就删掉，不在就剪枝，剪枝的时候需要注意需要把加入非法节点所删掉的距离加回来

  • 过程

bk-2

Stick Problem

Idea:

Coding

    bool Backtracking (int i) { // i 一般是表示当前的答案集合中已经包含i个元素了
        Found = false;
        if (i > N)
            return true;  // solved with (x1, ..., xN)
        for (each xi in Si) {
            // check if satisfies the restriction R
            OK = Check((x1, ..., xi), R);  // pruning 假设我加入xi后查看是否满足条件
            if (OK) {
                Count xi in; // 将xi加入答案集合
                Found = Backtracking(i + 1);
                if (!Found)
                    Undo(i);  // recover to (x1, ..., x{i-1}) // 如果我加入xi后没有找到解，那么就恢复到加入xi前的状态
            }
            if (Found) break; 
        }
        return Found;
    }

Minimax Strategy

Question

以井字棋为例

Minimax Strategy 中很重要的一个思想在于博弈，即在当前状态下，我作为当前玩家，我应该怎么走，才能使得我赢，而进行操作的判断条件之一就是对当前状态的评估，我们称这个评估函数为evaluation function

比如这样一种评估函数：

\[ f(P) = W_{computer} - W_{human} \]
\[ \text{where } W \text{ is the number of potential wins at position } P \]

在井字棋游戏中，我们可以这样实例化：

  • 将\(W_{computer}\)定义为假如现在人类不进行任何操作，计算机可能的获胜方式

这样我们在每一步操作之后，都可以得到一个当前状态的评估值，这个评估值就可以作为我们博弈树的节点

Key of Minimax Strategy

  • 在博弈树中，我们总是假设对方是理性的，即对方总是会做出最优的选择

这就是 Minimax 的来源：

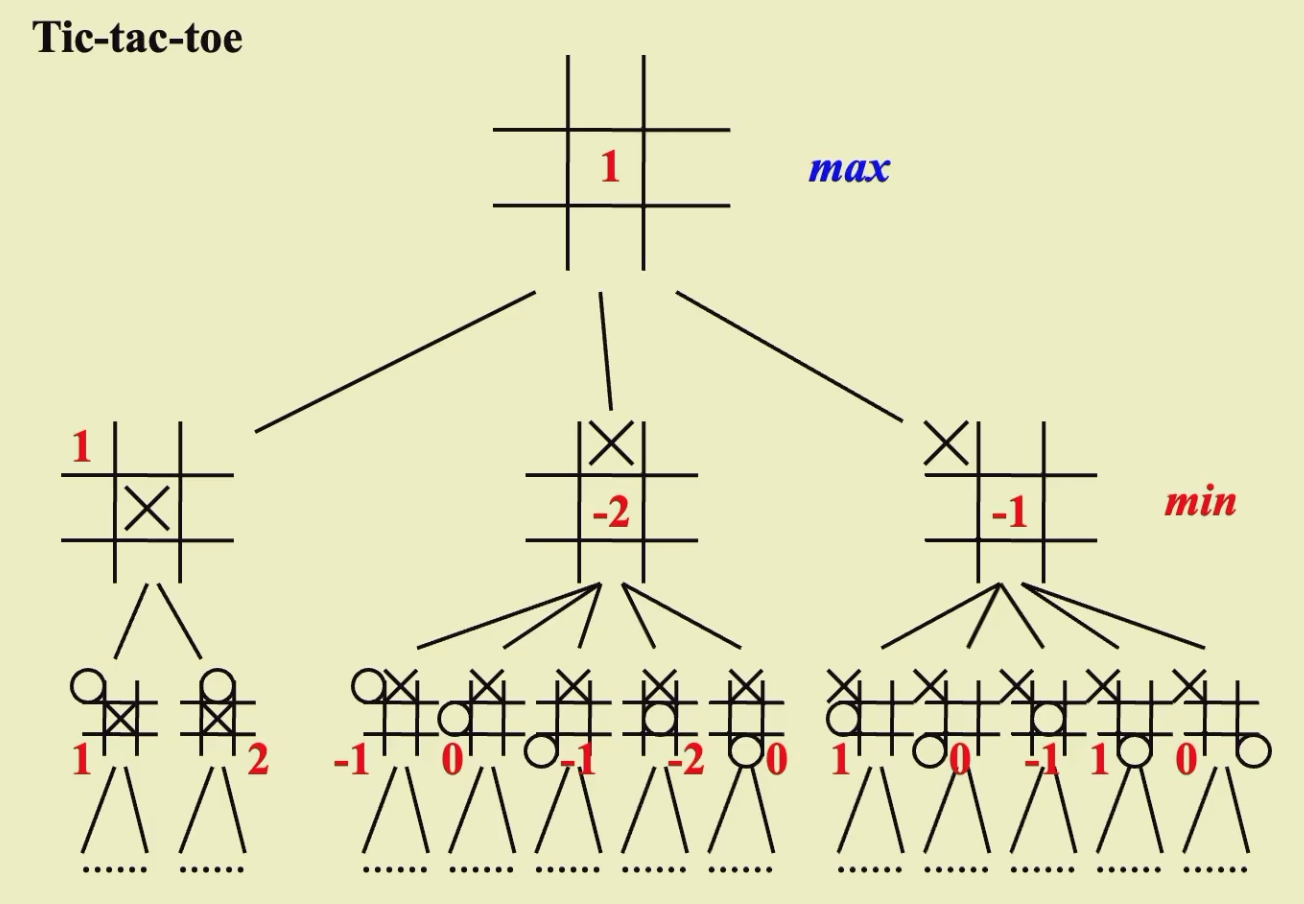
在自己选择的时候我们做\(f(P)\)的最大化，在对方选择的时候我们做\(f(P)\)的最小化

Example

bk-3

Alpha-Beta Pruning

\(\alpha - \beta\) Pruning 是 Minimax 的优化版本，他通过剪枝的方式将博弈树的搜索规模限制在\(O(\sqrt{N})\)个节点

  • \(\alpha\)剪枝：在如下的状态下我们不需要在进行?树的求算了
bk-4
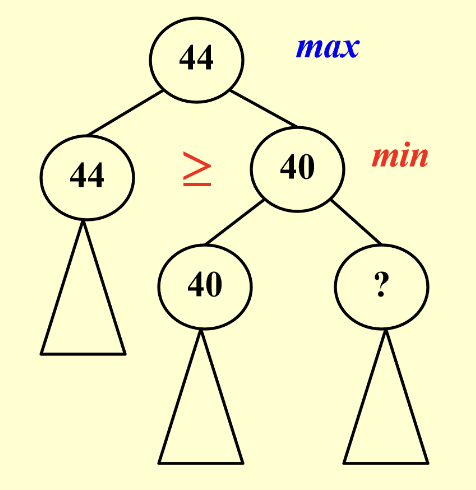
  • 在? >= 40(sibling)时，min节点不会采用这个大于四十的值
  • 在? < 40(sibling)时，min节点虽然会更新，但是max节点不会采用
  • \(\beta\)剪枝：在如下的状态下我们不需要在进行?树的求算了
bk-5
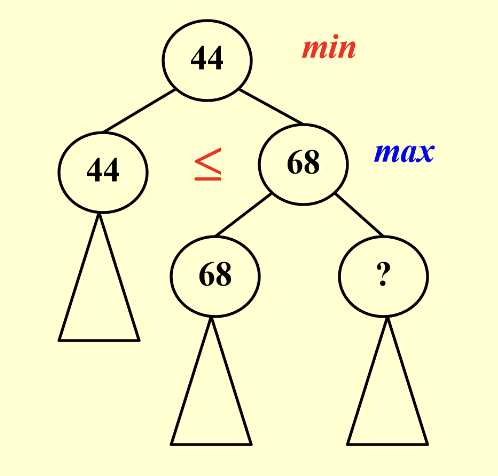
  • 在? <= 68(sibling)时，max节点不会采用这个小于等于68的值
  • 在? > 68(sibling)时，max节点虽然会更新，但是min节点不会采用