Skip to content

Divide and Conquer

核心思想：将较大的问题分解为较小的子问题，分别解决子问题，然后将子问题的解合并为原问题的解

Recursively:

Divide the problem into a number of subproblems

Conquer the subproblems by solving them recursively

Combine the solutions to the subproblems into the solution for the original problem

\[ T(n) = aT(n/b) + f(n) \]
\[ N 是原问题的规定大小, f(n) 是划分和合并子问题的解消耗的时间 \]

Example

Maximum Subarray

常见套路是均匀的一分为二

在这里，我们将数组一分为二，分别求出左半部分的最大子数组和右半部分的最大子数组，然后考虑跨越中点的最大子数组

横跨子序列的求算方法：

从中间向两边扫描，分别求出由中间向左的最大子数组和由中间向右的最大子数组，然后合并

Nearest Neighbor

平面上给定的N个点中找到距离最近的两个点

Solution

在先前的例子中，我们也采用了将问题均匀一分为二的方法，在这里，我们同样采用这种方法。

  • 首先根据这些点的x坐标，将这些点一分为二，分别求出左半部分和右半部分最近的两个点
  • 然后考虑跨越中点的最近两个点：
  • 如果考虑分割线左右两边所有的点，那么时间复杂度是\(O(N^2)\)，显然太大了
  • 我们第一步考虑的是选取一个束状带型区域，这个区域距离分割线的距离是\(\delta\)，则此时如果能保证这个区域中只有\(O(\sqrt{N})\)个点，那么我们就可以在\(O(N)\)的时间内找到跨越中点的最近两个点，但万一不呢？
  • 所以我们需要进一步的改进，再确定的垂直带状区域中，我们再选取一个竖直高度为\(\delta\)的的区域，这样构成了一个长为\(2\delta\)，宽为\(\delta\)的矩形
    dc-1
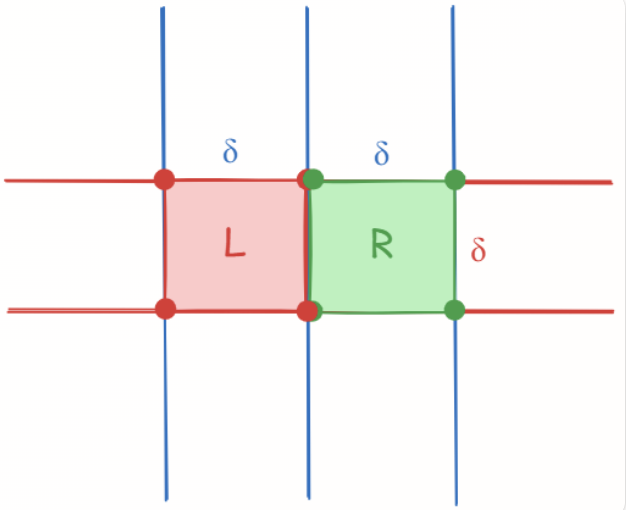
  • 在这个情况下，每个点只需要考虑与其他七个点（也就是边框的角上）之间的距离即可
  • 即使在所有点都在这个区域的情况下，因为每个点的判断次数是常数的，所以时间复杂度最差仍然是\(O(N)\)

Analysis

分治法的时间复杂度计算依托于我们先前定义的算式

\[ T(n) = aT(n/b) + f(n) \]

对于这种递归式，我们可以直接进行递归展开然后计算：

Example

\[ \begin{aligned} T(n) &= 2T(n/2) + N\\ &= 2(2T(n/4) + N/2) + N\\ &= 4T(n/4) + 2N\\ &= 4(2T(n/8) + N/4) + 2N\\ &= 8T(n/8) + 3N\\ &= ...\\ &= 2^k T(n/2^k) + kN\\ &= O(NlogN) \end{aligned} \]

Three Methods for Solving Recurrence

  • 假定\(\frac{n}{b}\) 是整数
  • 对于较小的n，我们假定\(T(n) = \Theta(1)\)
  1. Substitution Method

猜测一个结果，然后用数学归纳法证明

Warning

在进行这样的一个猜测时：

已知\(T(N) = 2T(\lfloor{N/2}\rfloor) + N\)，如果我们猜测\(T(N) = O(N)\)，那么我们会有如下的证明：

  • 假设对于\(m \leq N\)，结论成立
  • 那么存在一个常数\(c\)，取\(m = \lfloor{N/2}\rfloor\)，则有\(T(\lfloor{N/2}\rfloor) \leq c \lfloor{N/2}\rfloor\)
  • 将这个式子代入\(T(N) = 2T(\lfloor{N/2}\rfloor) + N\)，则有\(T(N) \leq 2c \lfloor{N/2}\rfloor + N = cN + N = O(N)\)

看起来似乎没有问题，但是在最后一个等式中，我们得到了\(cN+N=(c+1)N\)，这显然是\(O(N)\)的，但是在形式上它是错误的，因为我们预先假设正确的结论是\(T(m) \leq c m\)，所以要根据这个格式来证明出\(T(N) \leq cN\)，而不是\(T(N) \leq (c+1)N\)，必须保证精确的格式，常数项也必须一致

Tips

在时间复杂度递推中出现了类似\(T(\sqrt{N})\)的形式，可以采用换元来处理，这里的方法来源于noughtq同学的笔记：

  • 令\(m = \log2 N\)，那么\(T(\sqrt{N}) = T(2^{m/2})\)，\(T(N) = T(2^m)\)
  • 再令\(S(m) = T(2^m)\)，则有\(S(m/2) = T(2^{m/2}) = T(\sqrt{N})\)
  • 这时候我们就可以将\(T(N)\)的递推式转换为\(S(m)\)的递推式：\(S(m) = 2S(m/2) + 　m\)
  1. Recursion-tree Method

画出一些例子，用树表示递归的展开

在树中，每个非叶子节点表示的是向上递归时所需要消耗的时间，也就是公式中的\(f(n)\)，而叶子节点表示的是递归的结束，也就是\(T(1)\)

  • 我们在运算时假设了这棵树的开销就是每个节点的开销之和:
  • 第一部分是叶子结点的\(T(1)\)开销之和
  • 第二部分是所有非叶子节点的递归合并开销之和
Example

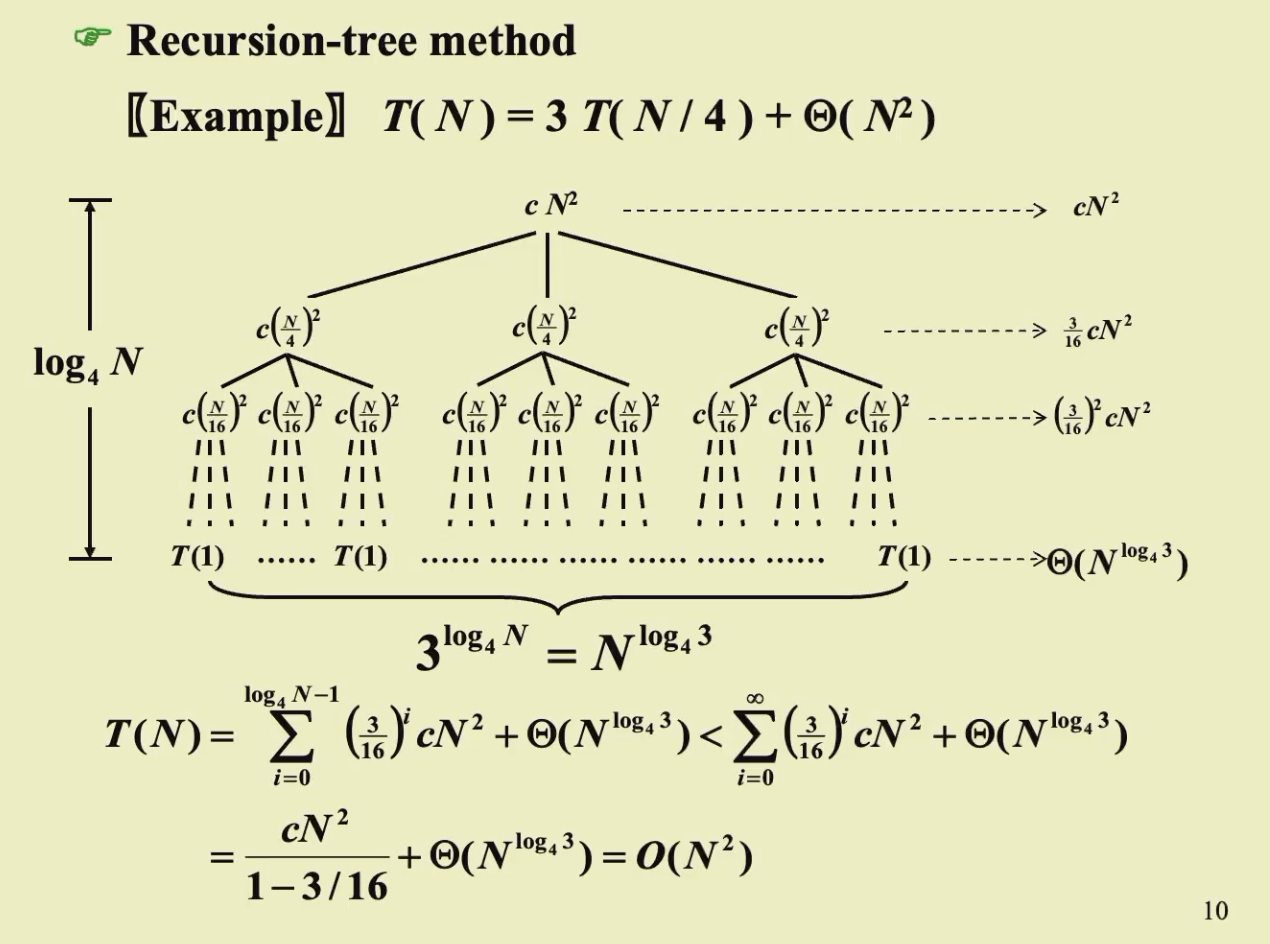
recursion-tree

  • 递归树的作用不是为了能够得到最准确的证明，而是为了能得到一个好的猜测，之后再用Substitution Method来严格证明

进行猜测的时候一般会进行一个放大的猜测，可能与真实的相同，也可能比真实值大，但一定不能比真实值小（那样就不用证了，肯定错了），所以对于无法画出树的全貌的例子一般放大一点猜测是没有问题的

  1. Master Method

先给出公式：

Master Method

  1. If \(f(n) = O(N^{\log_b a - \epsilon})\) for some constant \(\epsilon > 0\), then \(T(n) = \Theta(N^{\log_b a})\)
  2. If \(f(n) = \Theta(N^{\log_b a})\), then \(T(n) = \Theta(N^{\log_b a} \log N)\)
  3. If \(f(n) = \Omega(N^{\log_b a + \epsilon})\) for some constant \(\epsilon > 0\), and if \(af(n/b) \leq cf(n)\) for some constant \(c < 1\) and all sufficiently large \(n\), then \(T(n) = \Theta(f(n))\)

yy哥的形象解释，我觉得很有帮助（至少对于记忆来说）：

  • 在分析算法性能时一定要找到占主导的部分--我们从树的角度出发:

    • 如果我们的树长得非常霸气，巨高，叶子巨多无比，这时候时间开销被叶子dominate了，用Master 1，时间开销就是\(\Theta (N^{\log_b a})\)——也就是叶子的个数
    • 如果我们的树身材非常匀称，一片欣欣向荣，用Master 2，时间开销就是\(\Theta (N^{\log_b a} \log N)\)——也就是每一层的开销乘以树的高度
    • 如果我们的树根特别大，也就是说合并问题所需的时间非常多，甚至比第一层划分节点所需要的时间还要多（就是正则式的意义）用Master 3，时间开销就是\(\Theta (f(N))\)——也就是树根的值

我们发现这个公式并没有cover到所有情况的，就比如Master 3中，如果根很大，但是划分问题也很慢，就没办法用主方法了，所以主方法适用的情况就是三个很极端的情况

加强版的Master Method

当\(a \geq 1, b > 1, p \geq 0\)时，方程

\[ T(n) = aT(n/b) + \Theta(N^k \log^p N) \]

的解为：

\[ T(n) = \begin{cases} \Theta(N^{\log_b a}) & \text{if } k < \log_b a\\ \Theta(N^k \log^{p+1} N) & \text{if } k = \log_b a\\ \Theta(N^k \log^p N) & \text{if } k > \log_b a \end{cases} \]