Deep Generative Models¶

约 4093 个字 12 张图片预计阅读时间 14 分钟

Abstract

生成式模型被广泛应用于视频图像生成、文本生成、语音生成等领域，我在25年初（寒假）开始进行这部分的学习，主要参考的是Stanford CS236 课程和MIT 6.S987 课程的讲义，还有我哥的笔记，Lilian Weng的博客、Yang Song的博客

进行这部分学习的初衷是在侯老师的实验室，我在秦睿师兄的指导下开展关于分子生成工作的评测，由于不想局限于使用现有模型而是能更深入的理解模型的工作原理，因此开始进行这部分的学习。

在Diffusion和FlowMatching的学习中，我结合了MIT的6.S184课程，这门课提供了视频讲解+详细笔记+代码作业（赞👍，更重要的是他从Application角度进行了部分授课，包括热门的AIGC以及我将来想尝试的Protein Design！（这两部分我可能会多一些代码的学习尝试🤪

同时Stanford CS236还有一节课专门讲了Evaluating Generative Models，这是我认为在GenAI发展如此迅速的时代一件最有意义的一件事（之一）:

how to evaluate your model?

Intro¶

我们说生成式模型（Generative Model），与之相对的是判别式模型（Discriminative Model）：

Discriminative：

sample \(x \rightarrow\) label \(y\)

只有一个期望输出
Generative：

label \(y \rightarrow\) sample \(x\)

有多个期望输出

x and y

在chatbot中，\(y\)是prompt，\(x\)是response
在蛋白质生成中，\(y\)是性质/约束，\(x\)是蛋白质结构

并且利用贝叶斯公式我们可以由生成式模型的概率得到判别式：

\[ p(y|x) = \frac{p(x|y)p(y)}{p(x)} \]

但是反之并不能很好的成立：

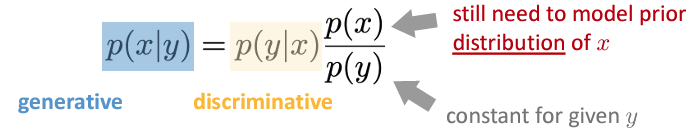
因为我们需要知道数据sample的分布，但是只有生成式概率\(p(x|y)\)，而\(p(x)\)是不知道的。

总结

生成式模型就是要去寻找数据的潜在分布\(p(x)\)，来生成与真实数据分布相似的样本

Probabilistic Modeling¶

前文中我们提到了一系列概率\(p\)，但是这些概率是哪里来的呢？

Hint

Probability is part of the modeling.

怎么理解这句话呢，我的理解就是我们在学习时，其实就是在学习一种概率分布，对观测的数据进行建模，所以其实得到的分布函数就是我们的模型。

这样说有点抽象，试着举个例子：

我们以生成式模型为例，采用概率建模的方法：

Image Generation

我们的目标是通过给定的一些图像，生成一个新的图像

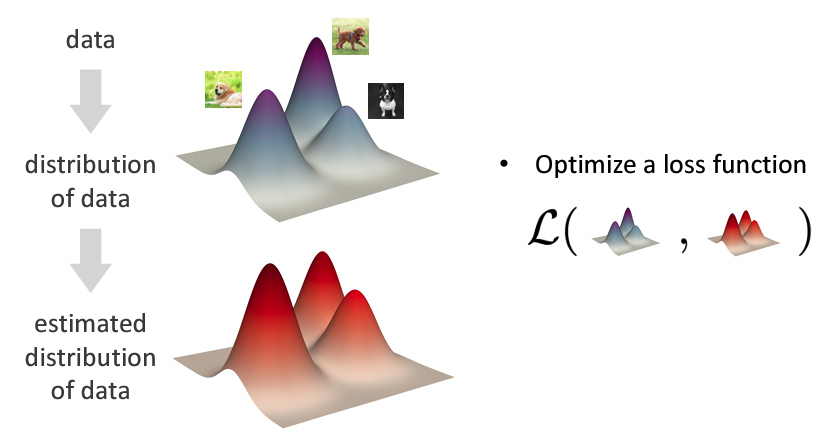
在通过一系列的方法，得到一个估计（estimated）的分布，这个分布的评估是通过损失函数\(L\)来进行的

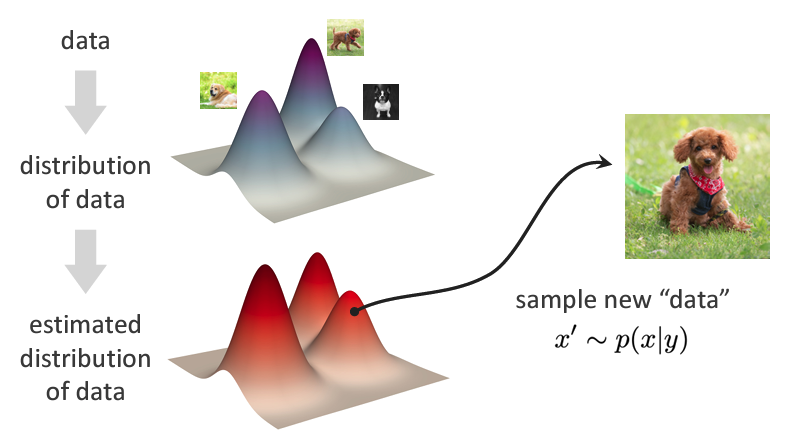
此时我们依照给定特征\(y\)，生成一个图像\(x'\)，这个\(x'\)就遵从我们得到的分布\(p(x|y)\)

Notes

Generative models involve statistical models which are often designed and derived by humans.
Probabilistic modeling is not just work of neural nets.
Probabilistic modeling is a popular way, but not the only way.

"Deep" Generative Models¶

深度学习是一种表征学习，也就是说我们学习的是如何将数据 \(x\) 映射到\(f(x)\)，使得损失函数\(L(f(x), y)\)最小。

在深度生成模型的学习中，我们学习的是如何表征概率分布

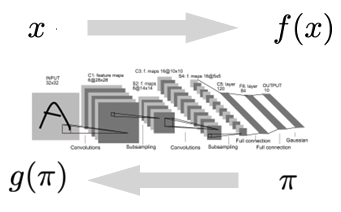
这里我们学习得到一个简单分布到复杂分布的映射，这个映射就是我们的模型。

\[ \pi \rightarrow g(\pi) \]

像这样：

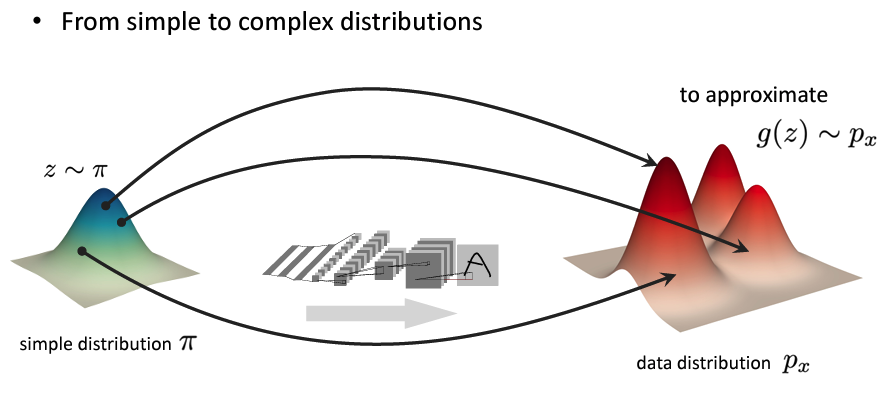
随后最小化基于数据的损失函数\(L(p_x , g(\pi))\)，得到模型\(g\)

总结

一个DGM可能包括：

Formulation：
- formulate a problem as a probabilistic modeling （进行概率建模）
- decompose a complex distribution into simpler and tractable ones （将复杂分布分解）
Representation：deep neural networks to represent data and their distributions （使用深度神经网络表示数据和他们的分布）
Objective function：evaluate the predicted distribution
Optimization：optimize the networks and/or the decomposition
Inference:
- sampler
- probability density estimator
- ...

Latent Variable Models¶

在这里我觉得需要提前说明的是，在深度生成模型中，我们经常使用隐变量（Latent Variables）

例如这样一组图片：

由于性别、年龄、肤色等等因素，图像\(x\)存在多种可能的变化，但除非图片是被注释annotated的，否则我们无法得知这些因素，或者说，这些因素是不可见的（not explicitly available）。

Latent Variable

这时我们的想法就是用隐变量\(z\)显示的建模来表示这些因素。

很直观的想法是用 Bayes 网络来表达：

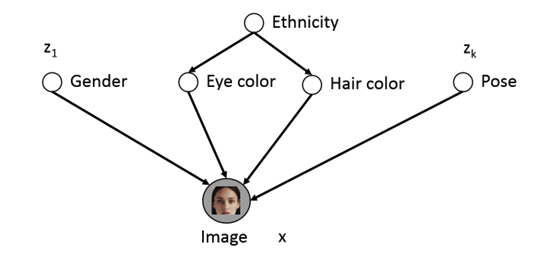
但是这其中的条件概率分布是很难得到的，因此我们使用神经网络来近似这个条件概率分布：

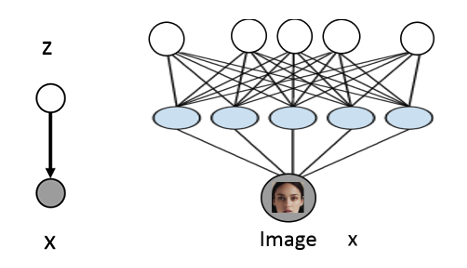
这时我们通常假设\(z\)是服从某种简单分布的，例如高斯分布：\(z \sim N(0, 1)\)

通过神经网络的处理，我们可以得到\(p(x|z)=N(x|\mu_{\theta}(z), \sigma_{\theta}(z))\)，在这里\(\theta\)是神经网络的参数。

我们希望在训练结束后，\(z\)可以表示\(x\)的潜在因素（特征）

使用\(z\)来表示有两点原因：

用潜变量可以简化问题
得到的潜变量本身就具有他的意义（不用在生成，用在推断或寻找特征）

Measure Distribution¶

在得到生成分布后，我们需要评估这个分布的优劣，这里对几个常用的评估方法进行介绍。

Divergence¶

给定两个概率分布\(P\)和\(Q\)，\(f\)-divergence定义为：

\[ D_{f}(P||Q) = \int {q(x)} f\left(\frac{p(x)}{q(x)}\right) dx \]

KL

KL 散度（Kullback-Leibler divergence）: 对于给定的两个分布\(p\)和\(q\)，KL散度定义为：

离散的：

\[ D_{KL}(p||q) = \sum_{x \in \mathcal{X}} p(x) \log \frac{p(x)}{q(x)} \]

连续的：

\[ D_{KL}(p||q) = \int p(x) \log \frac{p(x)}{q(x)} dx \]

可以看到KL散度是\(f\)-divergence的一种特殊情况，当\(f(x) = x \log x\)时，\(f\)-divergence就是KL散度。

非负性：\(D_{KL}(p||q) \geq 0\)
KL散度越小，两个分布越相似。
KL散度不具有对称性，即\(D_{KL}(p||q) \neq D_{KL}(q||p)\)

在对\(p_{\theta}\)和\(p_{data}\)进行比较时，我们取这两个变量的KL散度最小值：

\[ \min_{\theta} D_{KL}(p_{data}||p_{\theta}) \]

可以推导KL散度最小值等价于最大化期望对数似然（Maximum Log-Likelihood Estimation）：（用离散的KL公式，打开\(\log\)，其中\(p_{data}(x)\)是常数，所以可以忽略）

\[ arg\min_{\theta} D_{KL}(p_{data}||p_{\theta}) = arg\max_{\theta} \mathbb{E}_{x \sim p_{data}} \log p_{\theta}(x) \]

缺陷

由于我们忽略了\(p_{data}(x)\)的期望项，所以最终我们只能得到一个参数\(\theta\)的取值的估计，但是不能知道how close the model is to the true distribution。
In practice, we can't compute the true distribution \(p_{data}\)

对于第二个问题，我们为了避免涉及到\(p_{data}\)，我们使用另一种似然方法：经验对数似然（Empirical Log-Likelihood）

期望对数似然是对所有数据点的对数似然求期望，而经验对数似然是对所有数据点的对数似然求平均。

\[ \max_{\theta} \mathbb{E}_{x \sim p_{data}} \log p_{\theta}(x) \approx \max_{p_{\theta}} \frac{1}{N} \sum_{i=1}^{N} \log p_{\theta}(x_i) \]

这样我们就得到了所需要的最大似然估计。

对于数据的最大化似然：（联合概率似然）

\[ p_{\theta}(x^{1}, x^{2}, ..., x^{N}) = \prod_{i=1}^{N} p_{\theta}(x^{i}) \]

Fisher

Evaluating Generative Models¶

Key

What's the task that you really care about?

总的来说我们有以下几个任务：

Summary

Density Estimation
Compression
Sampling/Generation
Latent representation learning
Composition tasks

Density Estimation or Compression¶

对likelihood进行建模，就是将数据分割为train、val、test，用train进行训练的到\(p_{\theta}\)，然后用val进行tuning，最后用test进行评估：\(E_{p_{data}}[log p_{\theta}(x)]\)，这里的\(p_{data}\)是真实的数据分布，这个期望用于衡量\(p_{\theta}\)对真实数据的拟合程度，当\(p_{\theta}\)和\(p_{data}\)越接近，这个期望越大，两者相等时，这个期望就是真实数据的熵。

这里就引入了熵的概念，也是为什么我们有压缩即评估的说法

在压缩中，我们希望出现频率越高的数据，压缩后的长度越短，而出现频率越低的数据，压缩后的长度越长，我们在测试集上评估压缩后的平均长度，这个平均码长正是上文中期望的值（内部是负对数），这个值越小，说明模型越好。

一个例子就是对语言模型来说：

\[ \text{Perplexity} = 2^{-\frac{1}{D}E_{p_{data}}[\log p_{\theta}(x)]} \text{ for } x \in \mathbb{R}^D \]

Note

这里我的理解是，Compression对于模型来说，就是学习pattern，得到pattern后的模型，可以抛弃给定数据下pattern的输出，直接输出pattern，这样就去除了redundancy。

但问题是对于很多模型，我们是没有tractable likelihood输出的，例如GAN，VAE，EBMs，那我们怎么估计likelihood如果我们只有samples？

总的来说：

Unbiased estimation of \(p(x)\) from samples is impossible

所以我们要采用一些近似的方法，例如：

Kernel Density Estimation

给定一个Sample样本集合\(S=\{x_1, x_2, ..., x_n\}\)，我们希望估计一个不在\(S\)中的样本\(x_t\)的概率\(p(x_t)\)，有如下公式：

\[ \hat{p}(x_t) = \frac{1}{n} \sum_{i=1}^{n} K(\frac{x_t-x_i}{\sigma}) \]

其中\(K\)是核函数，\(\sigma\)是带宽参数bandwidth parameter

K 需要满足以下两条性质：
- 归一化：\(\int K(x) dx = 1\)
- 对称性：\(K(x) = K(-x)\)
Bandwidth parameter \(\sigma\) 需要选择一个合适的值(black)，如果\(\sigma\)太小，则估计的密度函数会过于尖锐(red)，如果\(\sigma\)太大(green)，则估计的密度函数会过于平滑。

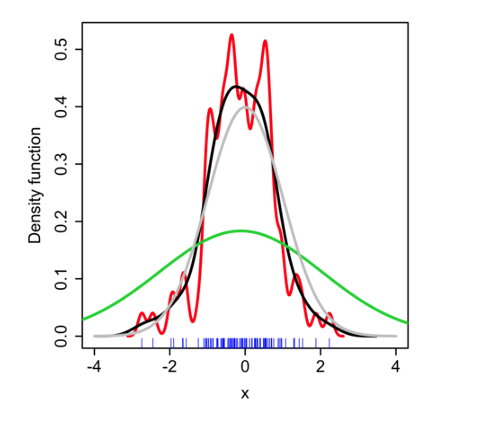
总的来说核密度估计是一种插值方法，通过对比待估计点与已知samples之间的距离，插值取值在用已知samples用核函数进行拟合的函数曲线上。

但是KDE的计算复杂度是\(O(n^2)\)，其在高维度上不可靠

Quantitative Evaluations¶

Inception Score¶

Inception Score 用于评估labelled data生成质量，主要考虑的是生成样本的sharpness和diversity

Inception Score

在IS中，我们有两点假设：

有标签的监督学习模型
具有好的分类器\(c(y|x)\)

Sharpness：

\[ S=\exp \left(E_{\mathbf{x} \sim p}\left[\int c(y \mid \mathbf{x}) \log c(y \mid \mathbf{x}) \mathrm{d} y\right]\right) \]

Diversity：

\[ D=\exp \left(-E_{\mathbf{x} \sim p}\left[\int c(y \mid \mathbf{x}) \log c(y) \mathrm{d} y\right]\right) \]

IS：

\[ \text{IS} = D \times S \]

对于这里清晰度和多样性的理解：

清晰度S：如果我们得到了一个非常清晰的图像，那么我们应该非常容易识别出一个图像的类别，这时分类器\(c(y|x)\)的分布应该是一个尖峰，也就是一个低熵的分布，所以我们用上述的S公式来求算分类器\(c(y|x)\)的熵，并追求他的最小化
多样性D：如果我们得到了非常多的类别，那么我们的边缘分布\(c(y)\)应该是接近一个均匀分布的形态，意味着每个样本出现的次数都差不多，所以\(c(y)\)的熵应该是一个高熵的分布，所以我们用上述的D公式来求算\(c(y)\)的熵，并追求他的最大化

如果还记得KL Divergence的定义，我们可以将IS公式改写为：

\[ \text{IS} = \exp \left(E_{x \sim p}\left[D_{KL}(c(y|x)||c(y))\right]\right) \]

这时maximize IS等价于最大化D和S之间的差异，也就是既要求模型生成清晰度高的图像，又要求模型生成多样性的图像，只有当两者都达到时，IS才会达到最大值

但是IS的问题在于：

依赖分类器
无法检测类内多样性

而且你会发现，好像IS并没有在考虑真实数据的分布，而是只考虑了生成数据的分布

Fréchet Inception Distance¶

FID的核心在于，与其间接地通过分类概率来评估，不如直接比较真实数据和生成数据在深度特征空间中的统计分布

FID Procedure

Feature Extraction

对于每一个真实数据\(x_r\)和生成数据\(x_g\)，输入进Inception V3模型提取特征，得到特征向量，这个向量不仅仅是浅层的分类，而是包含了更深层的特征，例如纹理、形状等，类似于一个特征指纹，这样我们得到了两组特征向量\(X_r\)和\(X_g\)
Fitting a Multivalue Gaussian

在这里FID做出一个假设：这两堆特征向量的分布可以用多元高斯来近似描述，这两个数据集分别具有他们自己的高斯属性：
- 均值向量\(\mu_r\)和\(\mu_g\)
- 协方差矩阵\(\Sigma_r\)和\(\Sigma_g\)
Fréchet Distance

计算两个高斯分布之间的距离：

\[ \text{FID} = ||\mu_r - \mu_g||^2 + \text{Tr}(\Sigma_r + \Sigma_g - 2(\Sigma_r \Sigma_g)^{1/2}) \]

在最后的式子中，第一项就是两个高斯分布均值之间的距离，第二项通过两个矩阵之间的trace衡量协方差矩阵的差异性

Kernel Inception Distance¶

在讨论FID的过程中，我们有一个关键的假设是数据的分布服从高斯分布，这会导致一些局限性。我们现在尝试直接比较两个数据分布本身：

KID

结合了Inception特征提取和核方法的分布差异度量MMD：

MMD：Maximum Mean Discrepancy，通过对比两个分布在再生核希尔伯特空间中的均值来衡量分布差异

\[ \operatorname{MMD}(p, q)=\sqrt{\mathbb{E}_{x, x^{\prime} \sim p}\left[K\left(x, x^{\prime}\right)\right]+\mathbb{E}_{y, y^{\prime} \sim q}\left[K\left(y, y^{\prime}\right)\right]-2 \mathbb{E}_{x \sim p, y \sim q}[K(x, y)]} \]

其中，\(K\)是核函数，\(x, x'\) 和 \(y, y'\) 分别是从分布\(p\)和\(q\)中独立采样的样本

对于整个表达式，第一二项用于衡量两个数据分布\(p\)和\(q\)的自相似性，第三项用于衡量两个分布之间的交叉相似性

KID Procedure
1. 特征提取：使用预训练的Inception网络提取特征
2. 计算MMD：计算生成数据\(p_g\)和真实数据\(p_r\)的MMD
3. 计算KID：
\[ \operatorname{KID}(p_g, p_r)= \operatorname{MMD}^2(Inception(p_g), Inception(p_r)) \]

常见的核函数有高斯核或者是计算高效的多项式核\(K(x, y) = (x^T y + c)^d\)

KID的优点：

避免了高斯分布假设
无偏估计
避免了trace计算
通过核函数隐含高阶统计量，有可解释性

对于有无偏估计我不是太清楚，这里放一些解释：

Bias vs. Unbiased

最直观的一个解释是：无偏估计是一个弓箭手能够围绕靶心进行射击，而偏差估计是弓箭手可以固定一个射击范围，但这个范围的中心不是靶心（系统性偏离真实值）

对于一个真实参数\(\theta\)，我们有估计量\(\hat{\theta}\)，我们定义无偏估计为：

\[ \mathbb{E}[\hat{\theta}] = \theta \]

而偏差估计为：

\[ \mathbb{E}[\hat{\theta}] \neq \theta \]

同时偏差量定义为：

\[ \text{Bias}(\hat{\theta}) = \mathbb{E}[\hat{\theta}] - \theta \]

对于实际任务来说：在小样本下有偏估计会系统性低估真实分布差异（偏差随样本量增大而减小），而无偏估计则不会因为样本量的变化而变化，但同时偏差的有无并不是绝对的好/坏，而是取决于任务本身，因为有的时候模型会需要降低方差不得不牺牲无偏性

Latent Representations¶

这是我认为的一个很困难的但是很核心的问题，并且这个问题是没有通解的。

有几个核心或者说常用的手段：

Clustering
Compression
Disentanglement

Disentanglement

解耦，我的理解就是将复杂多元系统拆解成单一变量控制的系统。

也就是说我们在潜空间中找到一个特定的潜变量，这个潜变量具有某种意义能够控制生成数据的某个特征，这样我们通过控制这个变量就能达到全局特征的修改

留言

欢迎在下方交流~